最初發布時間：2020-09-19 23:17:48
以前寫這篇文章，主要是接觸到一些非計算機學院的同學，為了交流方便我寫下了這篇文章……雖然現在回過頭來看寫得也比較草率，但確實是我對電腦的基礎操作的最早的認識，放到現在我絕對寫不出來哪個功能是最常用的了，因為我覺得哪個功能都常用。

github使用非常簡單，和百度一樣用就行，也支持下載上傳，多看看就能掌握基本操作，暫時不講，先說git。

git

1.下載

鏈接：https://pan.baidu.com/s/1-QimGqEr7fLtpfkSP35waA
提取碼：b9lm
以上是我自己在用的Git-2.11.1-64-bit。
在官網上下載也行，但是不推薦，因為官網下的也差不多，而且官網常常難以打開難以下載，容易鏈接失敗，點一年都不一定能生成下載鏈接。（個人體驗）
然后按默認選項安裝即可。

2.git內登錄github賬號

之后的不贅述，直接給鏈，廖雪峰大神講得比我好。由于還在入門，我們只想簡單知道git而不是立即搞事情，版本庫可以先不建。后面的如何回退也可以不用看。登錄成功就行。
https://www.liaoxuefeng.com/wiki/896043488029600/896067074338496

3.github上不太方便而git很方便做的某些事

git clone xxx

xxx是github下載按鈕處的鏈接。
還有的方便的就是用git刪文件。直接在本地庫上操作，再往上push一下就好了，這種需要建庫的事情請繼續看廖大佬的教程。
如果看不懂的話，或者說有些基礎指令有問題的話，請看下面的有關大學計算機基礎的教程。

大學計算機基礎

鏈接：https://pan.baidu.com/s/1-QimGqEr7fLtpfkSP35waA
提取碼：b9lm
以上還有我們計算機基礎的課件。
這個是講cmd之類的東西的，很多東西都是依賴這些指令的，所以建議隨便看看用用。
其實吧，說起來就這么幾條指令必用：

cd ..
cd Desktop
dir 

第一條，退回上一級目錄；
第二條，去下一級名字叫做Desktop也就是桌面的目錄；
第三條，展示當前目錄下的所有文件。

為什么說這三條是必備的，而不是刪除之類的呢？
第一二條讓你便捷地前后跳轉，而第三條讓你知道你現在能去哪。

一級一級跳轉有時候屬實不便，所以建議再會一條指令，cd 絕對路徑

絕對路徑：假設你已知能去的地方是長沙，同時假設最大的描述詞是地球，絕對路徑就是地球的中國的湖南的長沙。如E:\資料\大物\大物實驗。
相對路徑：假設你在中國，你想去長沙，相對路徑就是湖南的長沙。如大物\大物實驗。

前后跳轉以及隨便翻找就是我認為的文件結構了。

小彩蛋

1. win+R -> 輸入taskmgr ->方便清理后臺進程，檢查惡意彈窗廣告，還電腦清凈。
2. 在系統變量里的環境變量里添加某個文件夾，之后就可以直接用win+R并輸入這個文件夾的相對路徑，訪問這個文件夾的內容。也就是，如果把快捷方式全部放到一個文件夾里并且為它添加環境變量，就可以用鍵盤呼出應用和資料，不需要鼠標點點點，也不用把快捷方式放桌面上。

暫時想到這么多，之后再補充。【補充的都在網盤里了，可以自己看】

---

接下來順便再貼另一篇文章，我懶得貼成兩篇了，內容量不夠。

數組

參考文章

計算元素地址（i、j 均開始于 1）

• 主要是要分析出該元素前面有多少個(記為 n)元素，分析出來了即可知道下標為 n，LOC(i)=LOC(0)+size(L)*n。
• 分析過程：以行序或列序優先將矩陣中的元素依次排列。以按行序優先排列為例，假設 k 元素在第 i 行，則前面應至少有 x 個元素，再假設 k 在第 j 列，在當前行中前面應再有 y 個元素，從而得到 k 元素與 i、j 的對應關系。

按列序存放（高下標優先）

• 對于 A_m*n，有 LOC(i,j)=LOC(0,0)+(j*m+i)*sizeof(L)。
• 對于 A_abc，有 LOC(i,j,k)=LOC(0,0)+(k*a*b+j*a+i)*sizeof(L)。
• 同理可推至 n 維數組。

樹

參考文章

樹

• 非線性，一對多。（定義是遞歸形式的）

• 根（根結點的層為 1）、根的子樹、結點的度（結點的子樹數目）、葉子結點（也叫終端節點）、分支節點、雙親（雖然叫雙親但是 parent 只有一個）、樹的深度（又稱高度，葉子結點的層數）、兄弟、堂兄弟（同層不同雙親的結點）、祖先、子孫（所有子樹的結點）、有序樹（子樹的順序從左到右有限定，更換則不是同一顆樹）、無序樹。

• 森林：m 棵互不相交的數的集合，如 F={T₁,T₂,T₃}，任何一棵非空樹可表示為 Tree=(root,F)，F 是子樹森林。

  因為 root 根結點被拆掉了之后剩下的子樹就散了互不相交可以看作森林）

二叉樹

• 遞歸定義：根節點，左子樹右子樹。每個結點的孩子是不會重復的。
• 每個結點至多兩個子樹，是有序樹。
• 葉子結點的個數 n₀=度為 2 的結點數 n₂+1。（不直觀，需要記）

總數 n=n₀+n₁+n₂，孩子的個數=n-1=2n₂+n₁。

• 含有 n 個結點的二叉鏈表中，有 n+1 個空鏈域。

利用 n₀=n₂+1，空鏈域數=2n₀+n₁。

• 滿二叉樹：深度為 k 且有 2^k-1 個結點的二叉樹。

完全二叉樹

• 每個結點都和同深度的滿二叉樹中的編號從 1 至 n 的結點一一對應。其葉結點只可能出現在層次最大或者第二大的層上。結點數 2^k-1-1<n<=2^k。
• 對于完全二叉樹的第 i 個結點，若 2i>n，則該結點沒有左孩子結點；若 2i+1>n，則該結點沒有右孩子結點。若結點有雙親結點，則雙親結點的編號必然是 i/2 向下取整。

存儲結構

• 采用鏈式存儲結構比較方便。
• 三叉鏈表比二叉鏈表多一個指向雙親結點的指針。
• 靜態鏈表也可以用來描述二叉樹，此時的左孩子右孩子指針只要是孩子結點對應的標號（當然也可以是指針，但沒必要）就可以了，整體看起來是一個結構數組。

二叉樹遍歷：

D----訪問根節點，輸出根節點
L----遞歸遍歷左子樹
R----遞歸遍歷右子樹

1. 先序遍歷 DLR
2. 中序遍歷 LDR
3. 后序遍歷 LRD

隊列

參考文章

• 看完這篇你還不知道這些隊列，我這些圖白作了
• Java 中的 queue 和 deque 對比詳解

總結

• 隊列遵循 FIFO 原則，但是不一定以 FIFO 的方式排序各個元素。

非循環隊列

• 數據遷移只需要在 tail=MaxSize&&head!=0 時進行，以節省使用代價。
  

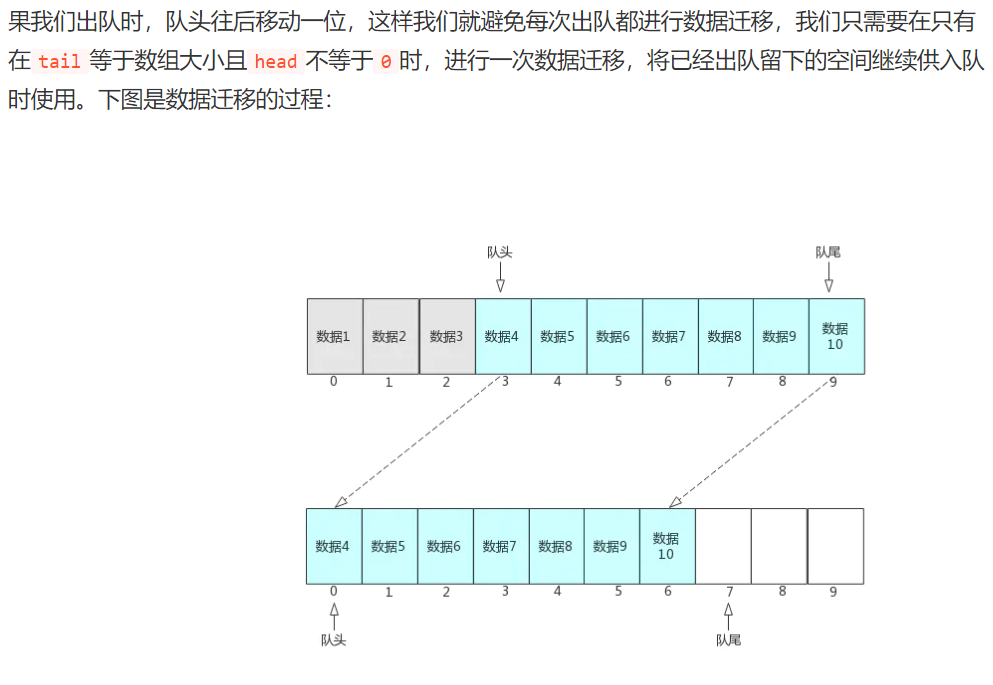
• 判斷隊列滿了的條件，tail = MaxSize,head = 0。

• 鏈式隊列與順序隊列比起來不需要進行數據的遷移，實現相對簡單很多，但是鏈式隊列增加了存儲成本。

循環隊列

• 對于一個存儲空間為 n 的循環隊列，只能存放 n-1 位數據，令 tail 與 head 重合時為隊空條件，(tail+1)%MaxSize==head 時為隊滿條件。
• 出入隊列都應該取模。比如入隊 tail=(tail+1)%MaxSize，出隊 head=(head+1)%MaxSize。
• 隊列長度 length=(tail-head+MaxSize)%MaxSize。一般隊列長度僅需要 tail-head，而循環隊列中，head 可能會比 tail 大，所以需要加上 MaxSize 并取模。
• 由長度公式以及隊滿條件知，顯然，循環隊列隊滿時 length 為 MaxSize-1。

雙端隊列（Deque）

• 隊頭、隊尾都可以進行入隊、出隊操作。總之它即有棧的功能，也有隊列的功能。
• 在將雙端隊列用作隊列時，將得到 FIFO 行為；在將雙端隊列用作堆棧時，將得到 LIFO 行為；

優先隊列（不遵循 FIFO）

• 從隊頭出隊，隊尾入隊。不過每次入隊時，都會按照入隊數據項的關鍵值進行排序。保證優先級最高的最先出隊。
• 一般用堆實現。

本賬號所有文章均為原創，歡迎轉載，請注明文章出處：https://shandianchengzi.blog.csdn.net/article/details/149937984。百度和各類采集站皆不可信，搜索請謹慎鑒別。技術類文章一般都有時效性，本人習慣不定期對自己的博文進行修正和更新，因此請訪問出處以查看本文的最新版本。