【重學數據結構】二叉搜索樹 Binary Search Tree

二叉搜索樹的數據結構

手寫實現二叉搜索樹

樹節點定義?

插入節點?

源碼?

流程圖?

?二叉樹插入步驟圖解

第一步: 插入 20?

第二步: 插入 10

第三步: 插入 30

第四步: 插入 5

查找節點?

源碼?

場景一: 查找成功 (search for 25)

第一步: 從根節點開始

第二步: 移動到右子樹

第三步: 找到目標

場景二: 查找失敗 (search for 12)?

第一步: 從根節點開始

第二步: 移動到左子樹

第三步: 繼續向右查找

刪除節點?

源碼?

核心刪除邏輯: delete(Node delNode)

BST 刪除節點實例圖解?

場景一: 刪除葉子節點 (Delete 5)?

場景二: 刪除只有一個孩子的節點 (Delete 15)

場景三: 刪除有兩個孩子的節點 (Delete 20)

第 1 步: 識別目標 (delNode) 與后繼 (miniNode)

第 2 步: 處理后繼節點的子樹 (第一次 transplant)?

第 3 步: 連接后繼節點與待刪節點的右子樹

第 4 步: 將后繼節點換到待刪位置 (第二次 transplant)

第 5 步: 連接后繼節點與待刪節點的左子樹 (最終狀態)

常見問題?

二叉搜索樹結構簡述&變T的可能也讓手寫

二叉搜索樹的插入、刪除、索引的時間復雜度?

二叉搜索樹刪除含有雙子節點的元素過程敘述?

二叉搜索樹的節點都包括了哪些信息

為什么Java HashMap 中說過紅黑樹而不使用二叉搜索樹 ?

二叉搜索樹的數據結構

二叉搜索樹（Binary Search Tree），也稱二叉查找樹。如果你看見有序二叉樹（Ordered Binary tree）、排序二叉樹（Sorted Binary Tree）那么說的都是一個東西。

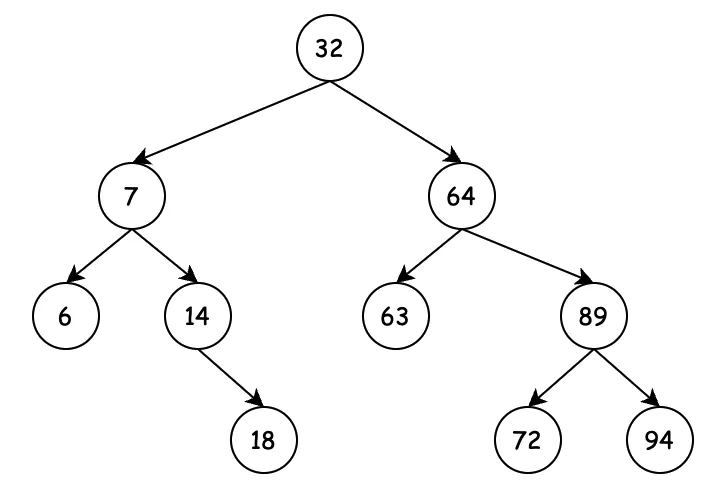
若任意節點的左子樹不空，則左子樹上所有節點的值均小于它的根節點的值；
若任意節點的右子樹不空，則右子樹上所有節點的值均大于它的根節點的值；
任意節點的左、右子樹也分別為二叉查找樹；?

手寫實現二叉搜索樹
?

樹節點定義?

public class Node {public Class<?> clazz;public Integer value;public Node parent;public Node left;public Node right;public Node(Class<?> clazz, Integer value, Node parent, Node left, Node right) {this.clazz = clazz;this.value = value;this.parent = parent;this.left = left;this.right = right;}@Overridepublic int hashCode() {final int prime = 31;int result = 1;result = prime * result + ((value == null) ? 0 : value.hashCode());return result;}@Overridepublic boolean equals(Object obj) {if (this == obj) return true;if (null == obj) return false;if (getClass() != obj.getClass()) return false;Node node = (Node) obj;if (null == value) {return node.value == null;} else {return node.value.equals(value);}}
}

插入節點?

源碼?

public Node insert(int e) {if (null == root) {root = new Node(e, null, null, null);size++;return root;}// 索引出待插入元素位置，也就是插入到哪個父元素下Node parent = root;Node search = root;while (search != null && search.value != null) {parent = search;if (e < search.value) {search = search.left;} else {search = search.right;}}// 插入元素Node newNode = new Node(e, parent, null, null);if (parent.value > newNode.value) {parent.left = newNode;} else {parent.right = newNode;}size++;return newNode;
}

流程圖?

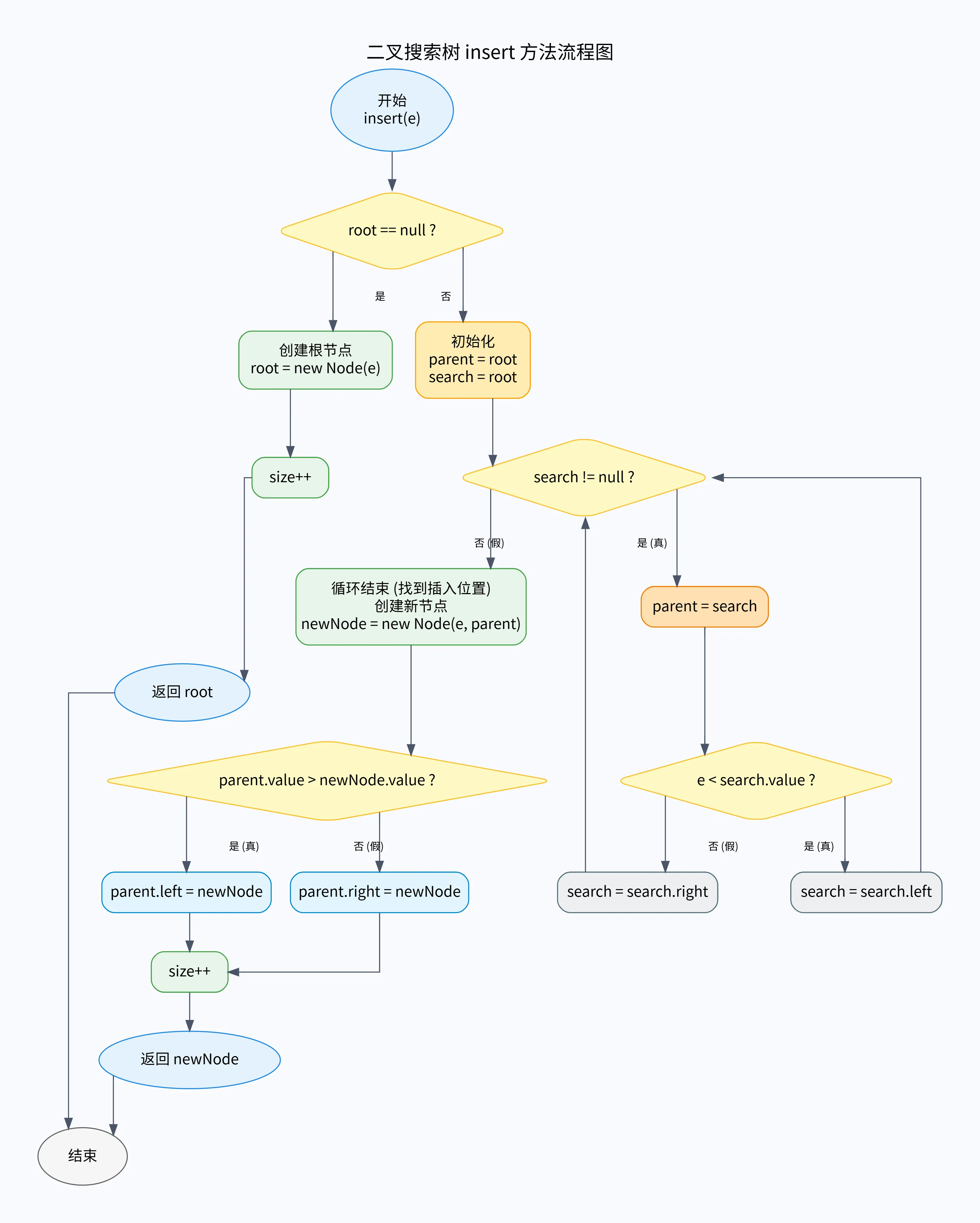
?二叉樹插入步驟圖解

以一個簡單的例子，依次插入數組 [20, 10, 30, 5] 中的四個數字，并畫出每一步操作后樹的結構變化。

第一步: 插入 20?

執行操作: 調用 insert(20)。
代碼路徑: 此時樹是空的，root 為 null。代碼執行第一個 if 分支，創建一個新的根節點，其值為20。

第二步: 插入 10

執行操作: 調用 insert(10)。
代碼路徑: root (20) 不為 null。進入 while 循環：

將 10 與根節點 20 比較，因為 10 < 20，所以 search 指針移動到左子節點 (當前為 null)。
search 變為 null，循環結束。此時的 parent 仍然是節點 20。
創建一個值為 10 的新節點，并將其作為 parent (節點20) 的左孩子。?

第三步: 插入 30

執行操作: 調用 insert(30)。
代碼路徑: root (20) 不為 null。進入 while 循環：

將 30 與根節點 20 比較，因為 30 > 20，所以 search 指針移動到右子節點 (當前為 null)。
search 變為 null，循環結束。此時的 parent 仍然是節點 20。
創建一個值為 30 的新節點，并將其作為 parent (節點20) 的右孩子

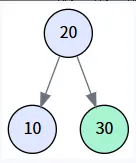
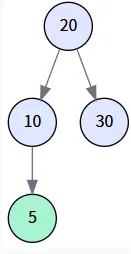
第四步: 插入 5

執行操作: 調用 insert(5)。
代碼路徑: root (20) 不為 null。進入 while 循環：

第1輪循環: 5 < 20，search 移動到左孩子 (節點10)。parent 更新為節點 20。
第2輪循環: 5 < 10，search 移動到左孩子 (當前為 null)。parent 更新為節點 10。
search 變為 null，循環結束。此時的 parent 是節點 10。
創建一個值為 5 的新節點，并將其作為 parent (節點10) 的左孩子。?

查找節點?

源碼?

public Node search(int e) {Node node = root;while (node != null && node.value != null && node.value != e) {if (e < node.value) {node = node.left;} else {node = node.right;}}return node;
}

初始樹結構
假設我們的樹通過依次插入 `[20, 10, 30, 5, 15, 25, 35]` 構建而成。

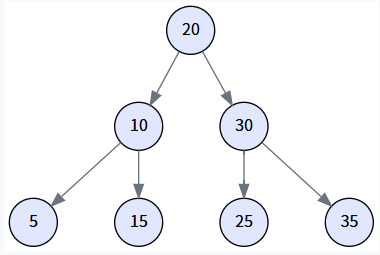
場景一: 查找成功 (search for 25)

我們來查找一個存在于樹中的值：`25`。?

第一步: 從根節點開始

當前節點 node: 20
比較: `25 < 20` 為假。
操作: 進入 `else` 分支，將 node 更新為其右孩子。node = node.right。

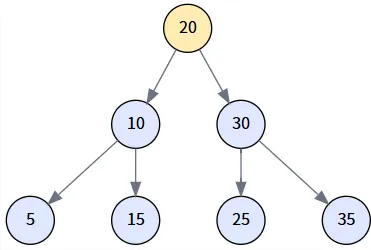
第二步: 移動到右子樹

當前節點 node: 30
比較: `25 < 30` 為真。
操作: 進入 `if` 分支，將 node 更新為其左孩子。node = node.left。

第三步: 找到目標

當前節點 node: 25
循環條件檢查: `node.value != e` (即 `25 != 25`) 為假。
操作: 循環條件不滿足，退出 while 循環。?

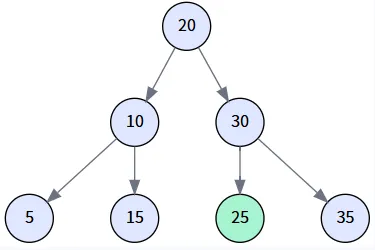
結果: 方法返回值為 25 的 Node 對象。?

場景二: 查找失敗 (search for 12)?

現在，我們查找一個不存在于樹中的值：`12`。

第一步: 從根節點開始

當前節點 node: 20
比較: `12 < 20` 為真，node 移動到左孩子 (10)。

第二步: 移動到左子樹

當前節點 node: 10
比較: `12 < 10` 為假。
操作: 進入 `else` 分支，node 更新為其右孩子。node = node.right。

第三步: 繼續向右查找

當前節點 node: 15
比較: `12 < 15` 為真。
操作: 進入 `if` 分支，node 更新為其左孩子。

?第四步: 到達葉節點末端

當前節點 node: `null` (因為節點 15 沒有左孩子)。
循環條件檢查: `node != null` 為假。
操作: 循環條件不滿足，退出 while 循環。

樹的結構保持不變，但我們的 node 指針現在是 null。

結果: 方法返回 null，表示未找到值為 12 的節點。?

刪除節點?

源碼?

public Node delete(int e) {Node delNode = search(e);if (null == delNode) return null;return delete(delNode);
}private Node delete(Node delNode) {if (delNode == null) return null;Node result = null;if (delNode.left == null) {result = transplant(delNode, delNode.right);} else if (delNode.right == null) {result = transplant(delNode, delNode.left);} else {// 因為刪除的節點，有2個孩子節點，這個時候找到這條分支下，最左側做小的節點。用它來替換刪除的節點Node miniNode = getMiniNode(delNode.right);if (miniNode.parent != delNode) {// 交換位置，用miniNode右節點，替換miniNodetransplant(miniNode, miniNode.right);// 把miniNode 提升父節點，設置右子樹并進行掛鏈。替代待刪節點miniNode.right = delNode.right;miniNode.right.parent = miniNode;}// 交換位置，刪除節點和miniNode 可打印測試觀察；System.out.println(this);transplant(delNode, miniNode);// 把miniNode 提升到父節點，設置左子樹并掛鏈miniNode.left = delNode.left;miniNode.left.parent = miniNode;result = miniNode;}size--;return result;
}
private Node getMinimum(Node node) {while (node.left != null) {node = node.left;}return node;
}private Node transplant(Node delNode, Node addNode) {if (delNode.parent == null) {this.root = addNode;}// 判斷刪除元素是左/右節點else if (delNode.parent.left == delNode) {delNode.parent.left = addNode;} else {delNode.parent.right = addNode;}// 設置父節點if (null != addNode) {addNode.parent = delNode.parent;}return addNode;
}

核心刪除邏輯: delete(Node delNode)

這是處理刪除操作的核心方法。它分為三個主要分支：

情況1: 要刪除的節點沒有左孩子。
情況2: 要刪除的節點有左孩子，但沒有右孩子。
情況3: 要刪除的節點有兩個孩子（最復雜的情況）。?

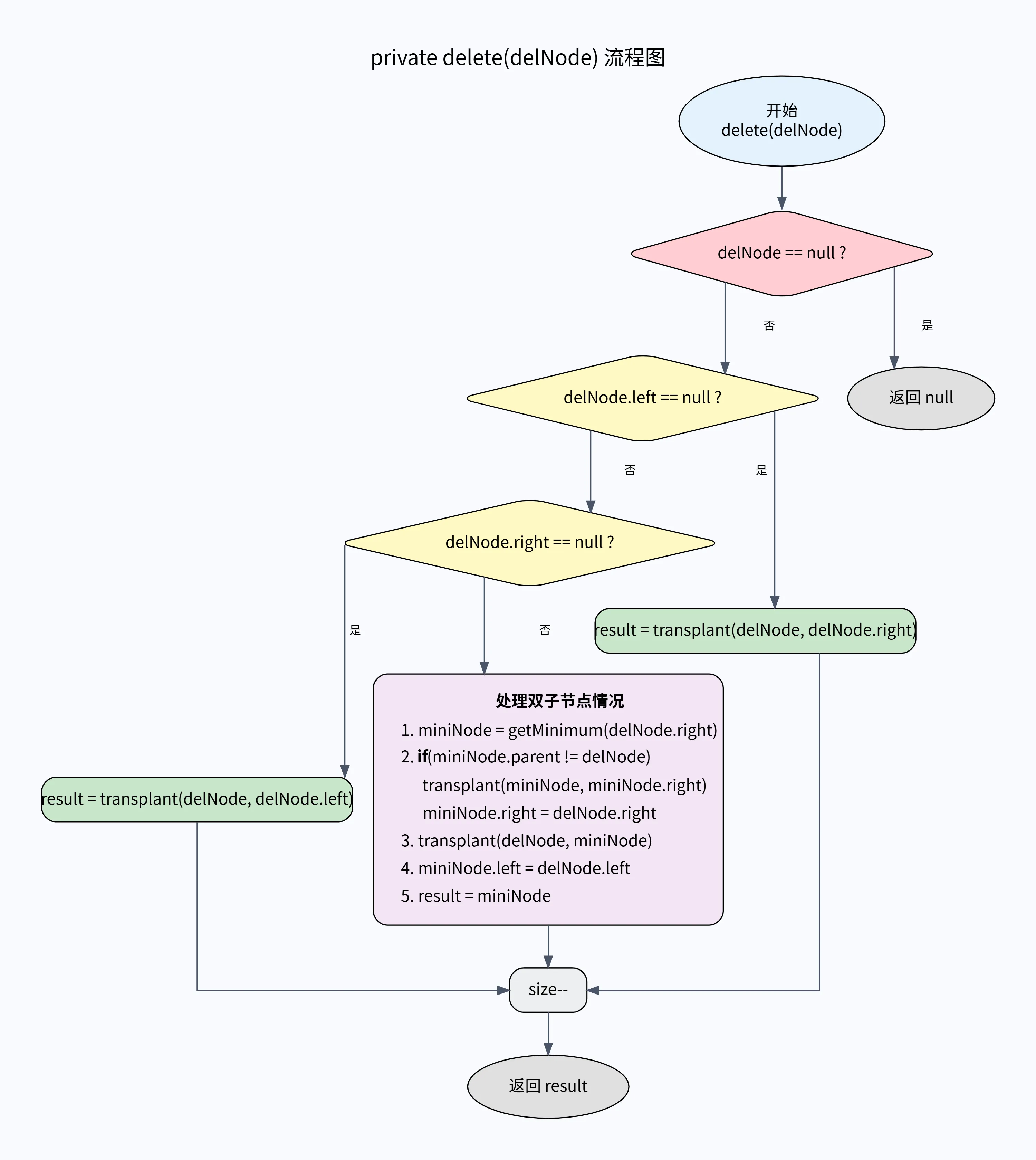transplant 方法是實現刪除的核心。它的作用是在樹中用一個節點 (addNode) 替換另一個節點 (delNode)，并正確地維護父節點的鏈接關系。它本身并不處理子節點的鏈接，這由 delete 方法完成。
getMinimum 是一個簡單的輔助方法，用于在給定的子樹中找到值最小的節點。它通過不斷地沿著左子節點向下遍歷直到末端來實現。

BST 刪除節點實例圖解?

我們將使用一個具體的二叉搜索樹來逐步演示刪除操作的三個場景。在圖示中：

紅色節點: 將要被刪除的目標節點 (delNode)。
黃色節點: 用于替換的后繼節點 (miniNode)。
紫色邊: 表示正在發生改變的父子鏈接。?

初始樹結構
我們的示例樹通過依次插入 `[20, 10, 30, 5, 15, 25, 35]` 構建而成。

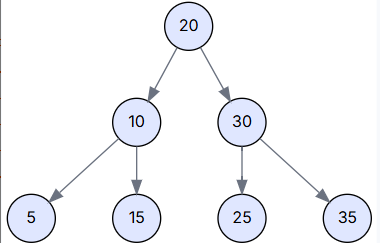
場景一: 刪除葉子節點 (Delete 5)?

執行步驟

delete(5) 調用 search(5) 找到節點 5。
進入 delete(Node delNode) 方法，delNode 是節點 5。
檢查 delNode.left == null 為真。
調用 transplant(delNode, delNode.right)，即 transplant(5, null)。
在 transplant 中，delNode 的父節點 (10) 的左孩子 (left) 被設置為 null。
刪除完成。

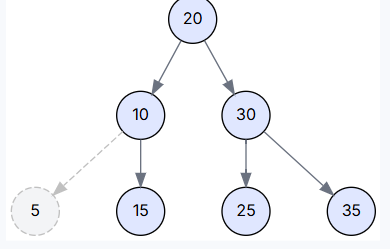
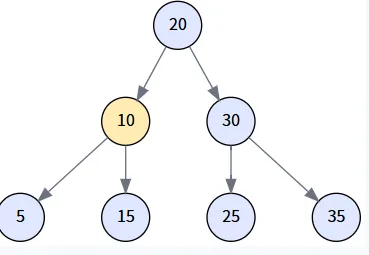
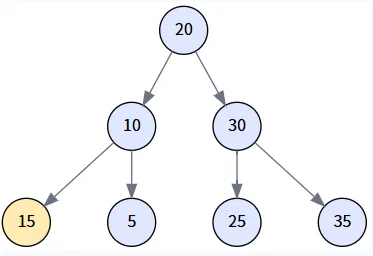
場景二: 刪除只有一個孩子的節點 (Delete 15)

注: 為演示此場景，我們創建一棵新樹 `[20, 10, 30, 5, 15, 35]`，其中節點 15 只有一個左孩子 5。我們會用它的子節點替換它。?

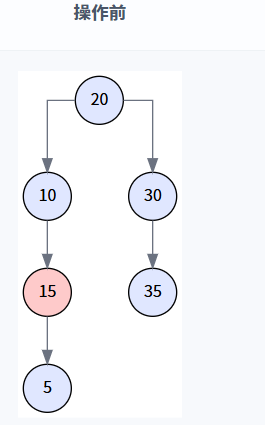
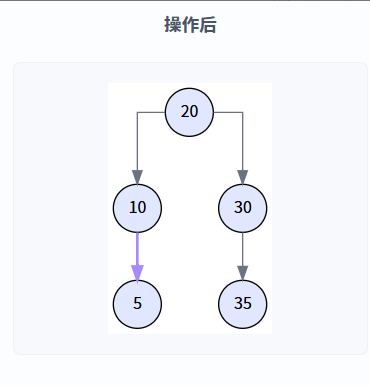
執行邏輯: transplant(15, 5) 被調用，節點 10 的右孩子指針直接指向了節點 5，同時更新了節點 5 的父指針。?

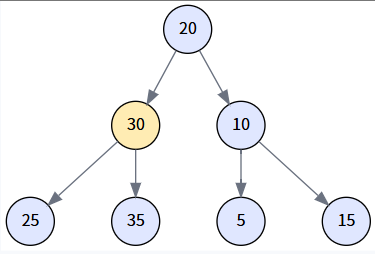
場景三: 刪除有兩個孩子的節點 (Delete 20)

這是最復雜的情況，我們將刪除根節點 20。這會觸發代碼中最完整的邏輯：尋找后繼節點 (右子樹的最小值)，并用它來替換被刪除的節點。

第 1 步: 識別目標 (delNode) 與后繼 (miniNode)

我們想刪除 20。因為它有兩個孩子，我們必須找到它的后繼節點。通過 `getMinimum(delNode.right)`，我們找到其右子樹 (以30為根) 的最小值，即 25。?

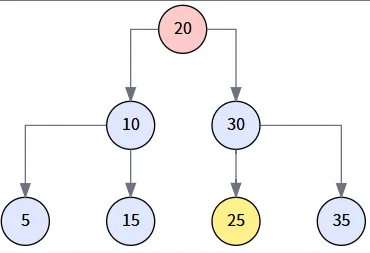
第 2 步: 處理后繼節點的子樹 (第一次 transplant)?

代碼檢查 `miniNode.parent != delNode` (即 30 != 20)，這個條件為真。因此，我們需要先將 `miniNode` (25) 提拔上來。我們調用 transplant(miniNode, miniNode.right)，即 transplant(25, null)，將 25 原來的父節點 (30) 的左孩子指向 25 的右孩子 (null)。

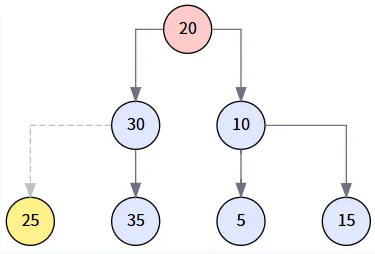
第 3 步: 連接后繼節點與待刪節點的右子樹

執行 miniNode.right = delNode.right。我們將 20 的右子樹 (以 30 為根) 變成 25 的右子樹。

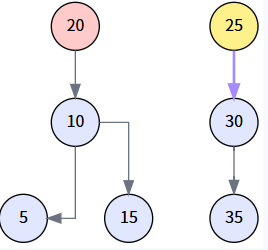
第 4 步: 將后繼節點換到待刪位置 (第二次 transplant)

調用 transplant(delNode, miniNode)，即 transplant(20, 25)。因為 20 是根節點，這會將樹的 root 指針更新為 25。

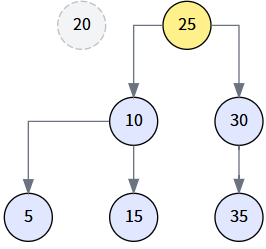
第 5 步: 連接后繼節點與待刪節點的左子樹 (最終狀態)

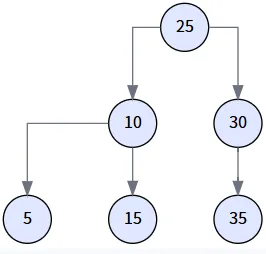
最后，執行 miniNode.left = delNode.left，將 20 的左子樹 (以 10 為根) 掛到 25 的左邊，完成整個刪除操作。?

常見問題?

二叉搜索樹結構簡述&變T的可能也讓手寫

某個節點的左子樹所有值都小于該節點，右子樹中所有值都大于該節點?

二叉搜索樹的插入、刪除、索引的時間復雜度?

插入、刪除、查找的時間復雜度取決于樹的高度

理想情況下是 O(log n), 但最壞情況下會退化為 O(n)?

二叉搜索樹刪除含有雙子節點的元素過程敘述?

刪除一個有兩個子節點的節點時，不能直接刪除掉它，而是從它的右子樹中找一個最小的節點（剛好比他大一點點），用這個節點來頂替他的位置。
例如：刪除節點 delNode 他有兩個子節點 delNode.left、delNode.right

從它的右子樹中找一個合適的節點來替代它 addNode
因為要用 addNode 節點來替換 delNode，所以需要先把 addNode 原來的位置清理干凈，最多只有一個右孩子（沒有左孩子），用右孩子來替換 addNode的位置
把delNode的父節點指向 addNode 、把delNode的左右子樹接到 addNode上面?