題目

給你一個字符串 s，請你將 s 分割成一些 子串，使每個子串都是 回文串 。返回 s 所有可能的分割方案。

思路

從題目中我們可以總結出這道題的三個需要解決的問題：

1. 如何判斷回文串
2. 如何找到一種方案里的所有回文子串
3. 如何找到所有可能的分割方案

解決了這三個問題我們就解決了這道題，我們先從最簡單的判斷回文串開始，想要判斷回文串我們只需要知道這個子串的開頭位置和結尾位置然后判斷字符串中兩者所代表的值是否相同再將開頭位置進行++結尾位置進行–來完成一個循環判斷即可。直到開頭位置大于等于結尾位置。
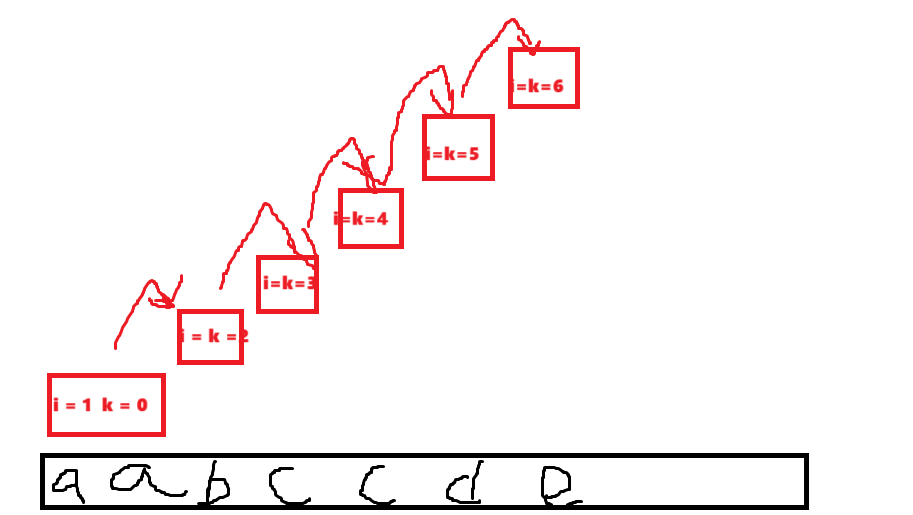
第一個問題解決了接下來我們來解決第二個問題，這里我們可以設計一個函數它的參數有兩個分別是當前位置的下標i和開頭位置的下標k，我們讓當前位置i不等于字符串的結尾位置之前都調用自身但是當前位置要+1只有在當前位置等于字符串的結尾位置時才開始判斷開頭位置k和當前位置i這一個子串是否是字符串如果是就插入到一個數組中如果不是就直接返回到上一個位置因為是上一個位置調用了函數才導致當前位置到結尾位置的。然后就是上一個位置進行判斷是否是回文串以此倒推直到找到回文串，之后呢我們再調用函數但是兩個參數都要變成i+1也就是把當前位置和開頭位置全部移到這個回文子串的下一個字符再進行判斷。我可以用一個圖來表示。

這樣我們就可以得到一個數組里面存著每一個回文子串。
接下來就是第三個問題如何找到所有方案，這里我們可以使用回溯的方法，有些同學在我們是調用自身來進行分割子串時就發現了這其實是典型的回溯的辦法，所以我們只需要在最后找到回文子串并且將其加入到數組中后再把這個回文子串進行pop掉就可以了。因為我們在i=n-1也就結尾位置后會和上圖一樣一層一層的調用自身直到i=n也就會存儲已經有著一種方案的回文子串數組了之后我們再一層一層的把插入的回文子串給pop掉這樣就可以繼續得到下一種方案了。

代碼

class Solution {
public:bool IsPalindrome(string& s , int left,int right){while(left < right){if(s[left++] != s[right--]){return false;}}return true;}vector<vector<string>> partition(string s) {int n = s.size();vector<vector<string>> res;vector<string> path;auto dfs = [&](this auto&& dfs,int i,int start){//當i=n時也就是一種方案的所有的回文串已經找完了if(i == n){res.emplace_back(path);return;}//一直到i = n-1也就是最后一個數if(i < n-1){dfs(i+1,start);}//從i處找到它的回文串if(IsPalindrome(s,start,i) == true){path.emplace_back(s.substr(start,i-start+1));//查找下一個位置的回文串dfs(i+1,i+1);//開始回溯path.pop_back();}};dfs(0,0);return res;}
};