CS231n-2017 Lecture7訓練神經網絡(二)筆記

本節主要是神經網絡的動態部分，也就是神經網絡學習參數和搜索最優超參數的過程

梯度檢查：

進行梯度檢查，就是簡單地把解析梯度與數值計算梯度進行比較，防止反向傳播的邏輯出錯，僅在調試過程中使用。有如下技巧：

使用中心化公式：

在使用有限差值近似計算數值梯度時，常見的公式是：

$\frac{df(x)}{dx} = \frac{f(x+h)-f(x)}{h}$ ?h是一個很小，近似為1e-5的數，但這個公式不常用且不好用

經常使用的是下方的中心化公式：

$\frac{df(x)}{dx} = \frac{f(x+h)-f(x-h)}{2h}$

該公式在檢查每個梯度的維度的時候，要求計算兩次損失函數，但梯度的近似值會準確很多，因為使用泰勒展開（這里假設原函數可以泰勒展開），則中心化公式的誤差近似 $O(h^2)$

使用相對誤差來比較：

比較數值梯度 $f^{'}_n$ 與解析梯度 $f_a^{'}$ 有哪些需要注意的細節，進而知道他們不匹配呢？

通常使用相對誤差來進行量化，即：

$\frac{|f_a^{'}-f_n^{'}|}{max(|f_a^{'}|,|f_n^{'}|)}$

當然，還必須注意兩個式子的梯度都為0的情況

量化閾值如下：

相對誤差>1e-2：通常意味著梯度出錯

1e-2>相對誤差>1e-4：較有可能出錯

1e-4>相對誤差：對有不可導點的目標函數可以接受，但若目標函數中沒有(tanh和softmax)，這個相對誤差還是太高

1e-7>相對誤差：認為正常

以上的浮點數運算都要使用雙精度浮點數

目標函數的不可導點(kinks):

在進行梯度檢查時，不可導點是導致不準確的原因之一，可能是由ReLU,SVM損失、Maxout神經元等引入，也就是x+h在不可導點的一側，而x-h在不可導點的另一側導致的。在計算損失的過程中，是可以知道不可導點有沒有被跨過的，在具有max形式的函數中持續追蹤保留梯度的變量身份，就可以實現這一點，若在計算f(x+h)和f(x-h)的時候，至少有一個變量其梯度保留情況變了，就說明不可導點被越過了，數值梯度會不準確

使用少量數據點：

解決上述不可導點問題的一個方法，因為含有不可導點的損失函數的數據點越少，在計算梯度時越過不可導點的概率就越小，所以使用少量數據點，可以使梯度檢查變高效

設置合適的步長h：

數值計算梯度的h并不是越小越好，當h特別小時，很可能會遇到數值精度問題，當梯度檢查出問題時，不妨將h調大一點，可能會恢復正常

梯度檢查的時間：

梯度檢查時在參數空間中的一個特定單獨點（往往隨機取）進行的，即使是在該點梯度檢查成功了，也不能馬上確保全局上的梯度實現都是正確的，且隨機的初始化可能不是參數空間中最優的代表性的點，這可能會導致梯度表面上正確實現。比如，SVM使用小數值權重初始化，就會把一些接近于0的得分分配給所有的數據點，而梯度將會在所有的數據點中展現出某種模式，不正確實現的梯度也許仍然能夠產生出這種模式，但是其無法泛化到更具代表性的操作模式，比如在一些數據點的得分比另一些要大的時候失效。因此，最好讓網絡學習先“預熱”一小段時間，等到損失函數開始下降之后，再進行梯度檢查。在第一次迭代就進行梯度檢查的話，若此時處于不正確的梯度邊界情況，無法被察覺，從而掩蓋了梯度沒有正常實現的事實

正則化蓋過數據損失：

Loss通常是數據損失和正則化損失的和，在某種情況，正則化損失的梯度有可能會遠大于數據損失，進而掩蓋掉數據損失梯度的不正確實現。因此，推薦先關掉正則化，單獨對數據損失做梯度檢查，然后再對正則化損失做梯度檢查

關閉Dropout和數據擴張(augmentation):

在進行梯度檢查時，需要關閉具有不確定效果的操作，比如Dropout和隨機數據擴展，否則會在計算數值梯度時導致巨大誤差。但是，關閉這些操作，會導致無法對這些操作進行梯度檢查，所以，更好的方法是在計算f(x+h)和f(x-h)之前，強制增加一個特定的隨機種子，確保偽隨機

檢查少量的維度：

實際模型中，梯度可以有上百萬的參數，這種情況下只能夠檢查其中的一些維度，然后假設其他維度是正確的，但是要確認在所有不同的參數中都抽取一部分來梯度檢查，比如可能偏置會占掉權重矩陣的一部分，則隨機有概率只隨機到偏置參數

進行參數學習之前的合理性檢查：

1.尋找特定情況的正確損失值

在使用小參數進行初始化時，確保得到的損失值與期望一致。最好先單獨檢查數據損失（令正則化損失為0），若跑出來損失值與期望不一致，那么可能在初始化中就出了問題

2.提高正則化強度時，觀察損失值是否變大

3.對小數據子集過擬合：

在整個數據集進行訓練之前，嘗試在一個很小的數據集上進行訓練，然后確保能到達0的損失值，最好令正則化強度為0。除非能通過這一個過擬合檢查，否則對整個數據集進行訓練時沒有意義的。但是，能對小數據子集進行過擬合，不代表完全正確，仍有可能存在不正確的實現，比如，因為某些錯誤原因，數據點的特征是隨機的，這樣算法也有可能對小數據進行過擬合，但在整個數據集上訓練的時候，就不會產生泛化能力。

檢查整個學習過程：

在訓練神經網絡時，需要追蹤多個重要數值

在下方的圖表中，x軸通常表示周期(epochs)單位，該單位衡量了在訓練中每個樣本數據都被觀測過的次數的期望

損失函數：

訓練期間第一個要跟蹤的數字就是Loss，它在前向傳播時對每個獨立的batch數據進行計算

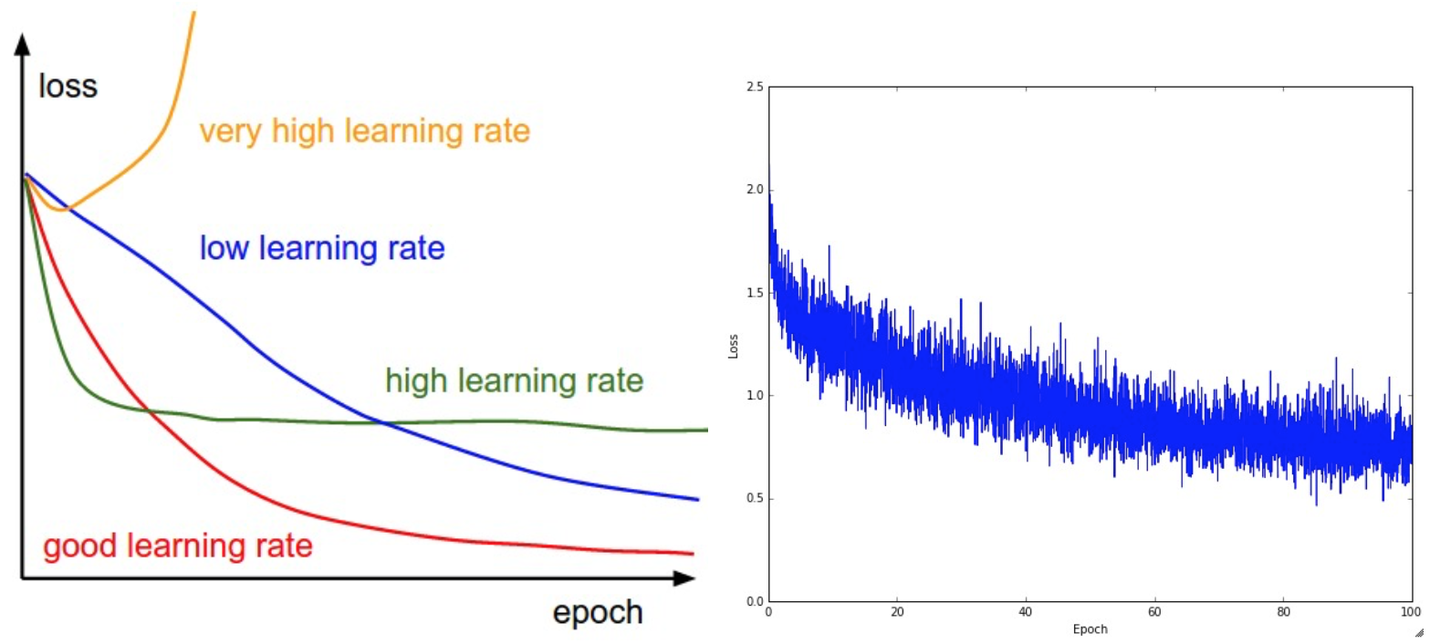
左圖不同曲線對應了不同學習率下loss隨epoch的變化，可以看到，過低的學習率導致loss的下降是現行的，高一些的學習率會看起來呈幾何指數下降。更高的學習率會使Loss下降得很快，但是接下來就會停在一個不好的損失值上（綠線）。這是因為最優化的能量太大，參數只能在混沌中隨機震蕩，無法最優化到一個很好的點上。

右圖顯示了一個經典的隨時間變化的損失函數值

損失值的震蕩程度和batch size有關，當batch size = 1時，震蕩會相對較大，當batch size 就是整個數據集時，震蕩就會最小，因為這時每次梯度更新都是在單調地優化Loss

訓練集和驗證集準確率：

在訓練分類器的時候，需要跟蹤的第二重要的數字就是驗證集和訓練集的準確率，這個圖表能夠使我們了解模型過擬合的程度

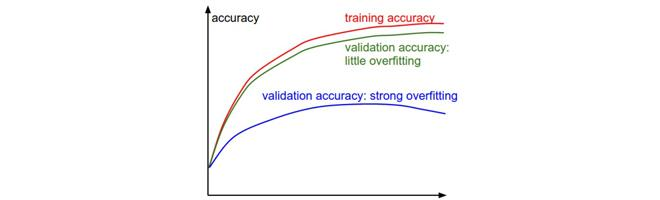
訓練集準確率和驗證集準確率之間的間隔指明了模型過擬合的程度，比如

藍色的驗證集正確率相較于訓練集正確率低了很多，就說明模型有很強的過擬合，遇到這種情況，就應該增大正則化強度，或者收集更多的訓練數據

另一種情況是驗證集曲線和訓練集曲線相近，這種情況說明模型參數容量不夠大，需要增大參數數量

權重更新比例：

最后一個需要跟蹤的量是權重中所有更新值的和與全部權重值之和的比例，一個經驗的結論是，這個比例應該要在1e-3左右，如果更低，說明學習率太小，如果更高，說明學習率過高

每層的激活數據及梯度分布：

一個不正確的初始化可能使學習過程變慢，甚至停止。其中一個檢查方法就是輸出網絡所有層的激活數據和梯度的柱狀圖，直觀的來說，如果看到任何奇怪的分布情況，那很可能有異常。如，對使用tanh的神經元，我們應該看到激活數據的值在整個[-1,1]區間中都有分布，如果看到神經元的輸出全都是0，或者全都聚集在-1/1，那就肯定有問題了

第一層可視化：

如果數據是圖像像素數據，那么把第一層特征可視化會有幫助，如圖：

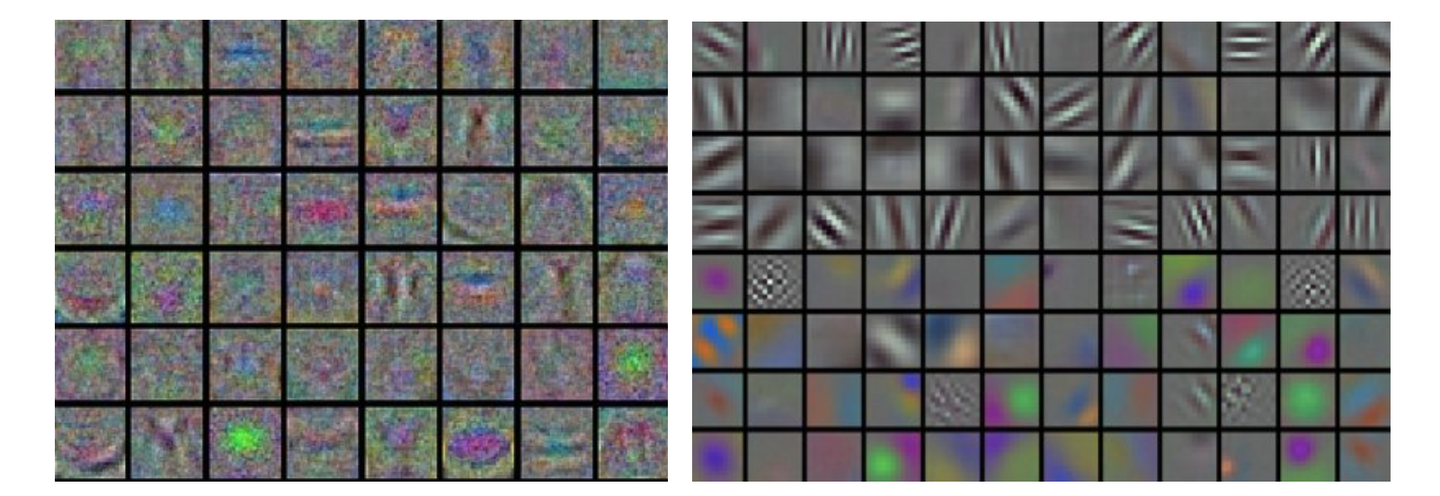
這是將神經網絡第一層權重可視化的例子，可以發現左側的特征中充滿了噪聲，這暗示網絡可能出現了問題：網絡沒有收斂、學習率設置不恰當，正則化懲罰的權重過低等

而右圖的特征就不錯，平滑干凈且種類繁多，說明訓練過程良好進行

參數更新：

在能使用反向傳播計算梯度的前提下，梯度就能夠被用來進行參數更新了

隨機梯度下降及各種更新方法：

普通更新：

最簡單的更新形式就是沿著負梯度方向改變參數（因為梯度指向的是上升方向，但我們通常希望最小化損失函數），假設有參數向量x和梯度dx，則簡單的更新形式為：

x+= - learning_rate * dx

動量(Momentum)更新:

這個方法在深度網絡中幾乎總能得到更好的收斂速度

原理：

我們將Loss理解為山的高度（而重力勢能是U=mgh，所以有U正比于h），用隨機數字初始化參數等同于在某個位置給質點設置初速度為0，則最優化過程可以看作是模擬參數向量（質點）在地形上滾動的過程

因為作用于質點的力與梯度的潛在能量有關( $Fh = W = -U = -mgh \Rightarrow F=-\nabla U$ )，質點所受的力就是損失函數的負梯度，又因為 $F=ma$ ，所以負梯度與質點的加速度是成比例的。即梯度影響加速度，加速度影響質點的速度，速度再影響質點在山中的位置

更新形式：

v = mu * v - learning_rate * dx // 更新速度
x += v //更新位置

這里引入了一個初始化為0的變量v，和一個超參數mu，mu被看作動量（一般設置為0.9），其有效地抑制了速度，降低了系統的動能（即質點上次的速度方向會影響該次的速度方向）

mu通常設置為[0.5, 0.9, 0.95, 0.99]中的一個，動量隨時間慢慢提升有時能略微改善最優化的結果

Nesterov動量：

與不同變量不同，其核心思想是，觀察上文的動量公式，x會通過mu*v而稍微改變，而mu*v是在還沒計算梯度之前就已經確定的，我們可以將未來的近似位置x+mu*v看作是“預測未來”，x+mu*v這個點一定在我們等會梯度下降更新后要停止的位置附近，因此，我們不妨計算x+mu*v的梯度，而不是x的梯度

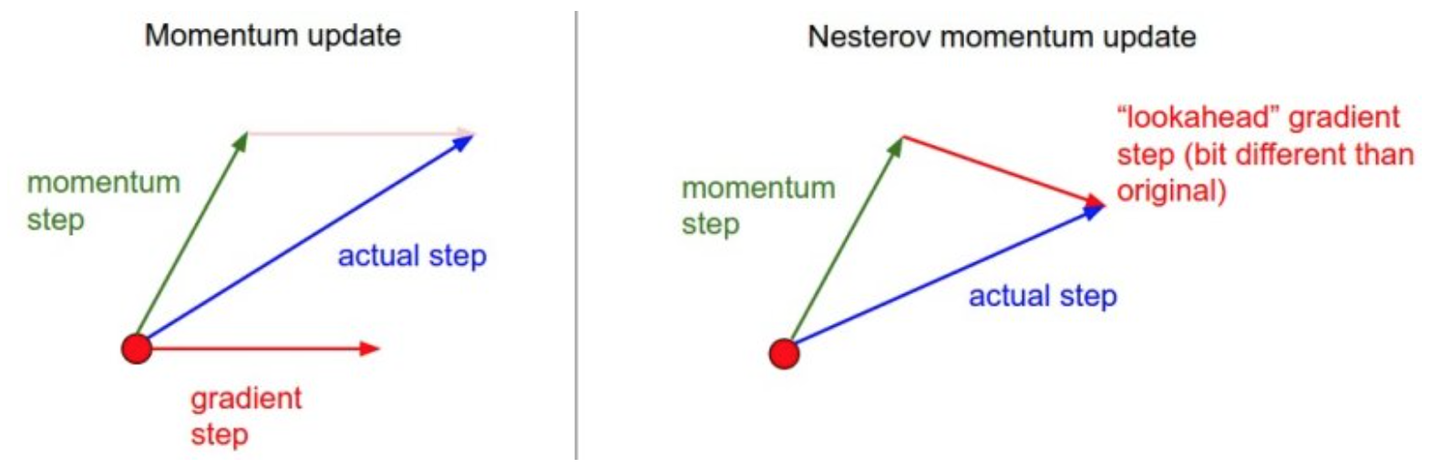
如圖所示，既然我們知道mu*v會把我們帶到綠色箭頭指向的點，我們就不在原地（紅色點）計算梯度了，我們在綠色箭頭所指的點計算梯度

#易于理解的實現版本
x_ahead = x + mu * v
v = mu * v - learning_rate * dx_ahead
x += v#實際實現版本
v_prev = v
v = mu * v - learning_rate * dx
x += -mu * v_prev + (1 + mu) * v

學習率退火：

在訓練深度網絡的時候，讓學習率隨著時間退火（逐漸減小）通常是有幫助的。因為如果學習率很高，系統的動能就過大，參數向量就會無規律地跳動，不能夠穩定到損失函數更深更窄的局部極值去。

實現學習率退火的方式：

1.隨步數衰減：

每進行幾個epoch就根據一些因素降低學習率。典型的是每過5個epoch就將學習率減少一半，或者每20個epoch將學習率減少到之前的0.1，具體數字設定嚴重依賴于具體問題和模型。

經驗做法：使用一個固定的學習率來進行訓練的同時觀察驗證集的錯誤，每當驗證集錯誤率停止下降時，就乘一個常數(例如0.5)來降低學習率

2.指數衰減：

公式為 $\alpha = \alpha_0e^{-kt}$ ，其中 $\alpha_0$ 為初始學習率，k是超參數，t是迭代次數，也可以使用epoch

3.1/t衰減

公式為 $\alpha = \frac{\alpha_0}{1+kt}$

在實踐中，隨步數衰減的dropout更受歡迎，因為它使用的超參數可解釋性比k更強，若有足夠的計算資源，可以讓衰減更緩慢一些，讓訓練時間更長

逐參數適應學習率方法：

前面討論的方法都是對學習率進行全局的操作，且對所有參數，其學習率都是一樣的，下面要介紹的方法是能夠適應性地根據參數來調整其對應的學習率，從而使得每個參數的學習率可能都不一樣。

Adagrad:

cache += dx**2
x += -learning_rate * dx / (np.sqrt(cache) + eps)

cache與梯度矩陣size一致，跟蹤了每個參數梯度的平方和，被用來歸一化參數更新步長（學習率），這樣一來，高梯度值的權重的學習率被減弱，低梯度值的權重的學習率被增強。平方根的操作非常重要，加入eps噪聲是為了防止除0，該算法的缺點是學習率單調變小通常過于激進，且過早停止學習

RMSprop:

是Adagrad的改進

cache = decay_rate * cache + (1 - decay_rate) * dx**2
x += - learning_rate * dx / (np.sqrt(cache) + eps)

decay_rate是取值在[0.9, 0.99, 0.999]的超參，cache變成了梯度平方的滑動平均，從而使學習率不會單調變小

Adam:

m = beta1 * m + (1 - beta1) * dx
v = beta2 * v + (1 - beta2) * dx ** 2
x += - learning_rate * m / (np.sqrt(v) + eps)

這里的更新方法和RMSProp很像，但其使用的是平滑版的梯度m

超參數調優：

訓練一個神經網絡會遇到很多的超參數設置，常用的有：

初始學習率

學習率衰減方式

正則化強度

實現：

更大的神經網絡需要更長的時間去訓練，所以調參可能幻幾天甚至幾周。一個設計代碼的思路是：

使用子程序持續地隨機設置參數，然后進行最優化，訓練過程中，子程序會對每個周期后驗證集的準確率進行監控，然后寫下一個記錄點日志。還有一個主程序，他可以啟動或者結束計算群中的子程序，根據篩選條件查看子程序寫下的記錄點，輸出它們的訓練統計數據，所謂海選。

比起交叉驗證，最好使用一個驗證集：

大多數情況下，一個size合理的驗證集可以使代碼更簡單

超參數范圍：

在對數尺度上進行超參數搜索，例如，一個典型的學習率搜索應該是這樣：

learning_rate = 10**uniform(-6,1)

這是因為如果只采取固定的線性步長分布的話，當學習率很小或者很大的話，步長對學習率的相對改變量差異是巨大的，所以我們采取對數尺度。但對于一些特別的參數（比如dropout），我們還是采取在原始尺度上搜索(dropout = uniform(0,1))

隨機搜索優于網絡搜索：

通常有部分超參數比其他超參數更重要，通過隨機化搜索，而不是網格化搜索，可以更精確地發現較重要的超參數的好數值

對于邊界上的最優值要謹慎：

這種情況一般發生在搜索范圍不好的情況，若我們得到的超參數較優值在搜索邊界上，我們就需要調整我們的搜索范圍

從粗到細地分階段搜索：

可以先進行粗略的范圍搜索，然后根據最優值出現的地方，縮小范圍進行搜索。進行粗搜索的時候，訓練一個epoch就可以了，因為很多超參數的設定會讓模型無法學習。搜索的范圍越精細，訓練的epoch越多