智靈班分班考 · Day1
時間線
- 8:00 在濱蘭實驗的遠古機房中的一個鍵盤手感爆炸的電腦上開考。
- 開 T1,推了推發現可以 segment tree 優化 dp,由于按空格需要很大的力氣導致馬蜂被迫改變。后來忍不住了頂著疼痛按空格。
- 8:30 過了樣例,但是沒有大樣例,先這樣吧。
- 開 T2,發現每顆子樹可以對應到序列上的一段區間,感覺可以區間 dp,但是怎么知道左右兒子的點的左右手寫上什么呢?
- 苦思冥想到 9:45,思考無果打算打一個暴搜,暴搜過程中發現狀態數可以直接從 O(n4)O(n^4)O(n4) 降到 O(n3)O(n^3)O(n3),但是我忘了轉移還要 O(n)O(n)O(n) 導致我以為我莫名其妙獲得正解,于是把暴搜加了個 O(n3)O(n^3)O(n3) 空間復雜度的記憶化數組(n≤500n\le 500n≤500)。
- 10:20 開 T3,一眼盯真,維護每個區間的支配點對,這只有 O(nlog?V)O(n\log V)O(nlogV) 個,然后轉二維數點;二維數點過程中推出了形如給定 [l,r][l,r][l,r],數 l≤u≤v≤rl\le u\le v\le rl≤u≤v≤r 的數量,腦子爆炸以為要數 (l,l)(l,l)(l,l) 到 (r,r)(r,r)(r,r) 的矩形,發明了一會兒二維 st 未果,最后注意到只要數 l≤u≤nl\le u\le nl≤u≤n,1≤v≤r1\le v\le r1≤v≤r 就可以了。
糖丸力 - 寫完調完 T3 是 11:10,趕緊開 T4,一眼盯真,對 dfn 序維護線段樹,線段樹每個節點維護一個 01 Trie,單點修改就修改一整條鏈,查詢正常查詢,時空復雜度 O(nlog?nlog?V)O(n\log n\log V)O(nlognlogV),趕緊沖!欸之前是不是過來說了啥 T4 某個樣例要改一改?算了不管了。
- 寫寫寫,11:45 分寫完,測樣例發現錯了(其實是因為樣例是錯的),以為自己讀錯題了,爆裂鼓手,遺憾離場。
期望得分 100+60+100+70,實際得分 30+0+100+0。掛了 200 分,天下無敵!
總榜排名第 50,下一場需要翻 20+ 名。
題解 & 錯因
T1
給定一個長度為 nnn 的數列 aaa,你需要選出若干個不相交也不相鄰的區間(即任意兩個區間中間至少隔一個元素),一個區間 [l,r][l,r][l,r] 能被選當且僅當 l=rl=rl=r 或者 ?i∈[l+1,r]\forall i\in[l+1,r]?i∈[l+1,r],滿足 ai≥∑j=li?1aja_i\ge\sum_{j=l}^{i-1}a_jai?≥∑j=li?1?aj?;求所有方案中區間中元素的最大和。
2≤n≤2×1052\le n\le 2\times 10^52≤n≤2×105,1≤ai≤1091\le a_i\le 10^91≤ai?≤109。
設 f(i)f(i)f(i) 表示考慮完 [1,i][1,i][1,i] 的答案。注意到以 aia_iai? 為選中區間右端點時,最長可選區間的左端點隨著 iii 增大單調不降,于是可以雙指針維護這個左端點。從 jjj 轉移的式子是 f(i)←max?k<j?1f(k)+∑k=jiakf(i)\gets \max_{k<j-1}f(k)+\sum_{k=j}^ia_kf(i)←maxk<j?1?f(k)+∑k=ji?ak?,令 si=∑j=1iais_i=\sum_{j=1}^ia_isi?=∑j=1i?ai? 那么就是 f(i)←max?k<j?1f(k)+si?sj?1f(i)\gets \max_{k<j-1}f(k)+s_i-s_{j-1}f(i)←maxk<j?1?f(k)+si??sj?1?,令 g(j)=max?k<jf(k)?sjg(j)=\max_{k<j}f(k)-s_{j}g(j)=maxk<j?f(k)?sj?,線段樹維護這個東西的區間最大值即可。時間復雜度 O(nlog?n)O(n\log n)O(nlogn)。
為啥我掛成 30pts 了呢?賽時 g(j)g(j)g(j) 的表達式錯誤的認為是 f(j?1)?sjf(j-1)-s_{j}f(j?1)?sj?,也就是堅定的認為只要隔一個元素。痛失 70pts。
#include <bits/stdc++.h>
bool MemoryST; using namespace std;
#define ll long long
#define mk make_pair
#define open(x) freopen(#x".in", "r", stdin), freopen(#x".out", "w", stdout)
#define lowbit(x) ((x) & (-(x)))
#define lson l, mid, rt << 1
#define rson mid + 1, r, rt << 1 | 1
#define BCNT __builtin_popcount
#define cost_time (1e3 * clock() / CLOCKS_PER_SEC) << "ms"
#define cost_space (abs(&MemoryST - &MemoryED) / 1024.0 / 1024.0) << "MB"
const int inf = 0x3f3f3f3f;
const ll linf = 1e18;
mt19937 rnd(random_device{}());
template<typename T> void chkmax(T& x, T y) { x = max(x, y); }
template<typename T> void chkmin(T& x, T y) { x = min(x, y); }
template<typename T> T abs(T x) { return (x < 0) ? -x : x; }const int maxn = 2e5 + 5;
int n, a[maxn]; ll sum[maxn];
ll f[maxn];
ll mx[maxn<<2];
// 一開始空格按的難受死了沒打空格
void update(int rt){mx[rt]=max(mx[rt<<1],mx[rt<<1|1]);
}void build(int l,int r,int rt){if(l==r){mx[rt]=-1e18;return;}int mid=(l+r)>>1;build(lson),build(rson),update(rt);
}ll query(int l,int r,int rt,int nowl, int nowr){if (nowl > nowr) return 0;if(nowl<= l && r <= nowr) return mx[rt];int mid = (l + r) >> 1; ll res = -1e18;if (nowl <= mid) res = max(res, query(lson, nowl, nowr));if (mid < nowr) res = max(res, query(rson, nowl, nowr));return res;
}
// 忍不住開始打空格
void modify(int l, int r, int rt, int now, ll k) {if (l == r) return mx[rt] = max(mx[rt], k), void(0);int mid = (l + r) >> 1;if (now <= mid) modify(lson, now, k);else modify(rson, now, k);update(rt);
}
bool MemoryED; int main() {scanf("%d",&n),build(0,n,1);for(int i=1;i<=n;i++)scanf("%d",&a[i]),sum[i]=sum[i-1]+a[i];modify(0, n, 1, 0, -sum[1]);modify(0, n, 1, 1, (f[1] = a[1]) - sum[2]);ll ans = a[1];for(int i=2,j=1;i<=n;i++){for(j<i;sum[i-1]-sum[j-1]>a[i];j++);f[i] = f[i - 1];if (j == 1) {chkmax(f[i], sum[i]);modify(0, n, 1, i, sum[i] - sum[i + 1]);} else {chkmax(f[i], query(0, n, 1, j - 2, i - 2) + sum[i]);modify(0, n, 1, i, f[i] - sum[i + 1]);} ans = max(ans, f[i]);}printf("%lld\n", ans);return 0;
}T2
給定一個長度為 nnn 的序列 aaa,對于所有中序遍歷為 1,2,??,n1,2,\cdots,n1,2,?,n 且是以點的編號為鍵值的二叉搜索樹,定義一個點 uuu 的權值是:從 uuu 到根節點的路徑中,深度最深的是父節點左兒子的父節點權值(若沒有則是 111)乘上深度最深的是父節點右兒子的父節點權值(若沒有則是 111),整棵樹的權值是所有點的權值的和。求所有樹的權值的最大值。
1≤n≤5001\le n\le 5001≤n≤500,1≤ai≤1071\le a_i\le 10^71≤ai?≤107。
注意到任意一個區間 [l,r][l,r][l,r] 都可以對應一個子樹。不妨我們指定 [l,r][l,r][l,r] 這顆子樹的根節點是 xxx(l≤x≤rl\le x\le rl≤x≤r),我們考察 xxx 是哪兩個父節點的權值乘積。
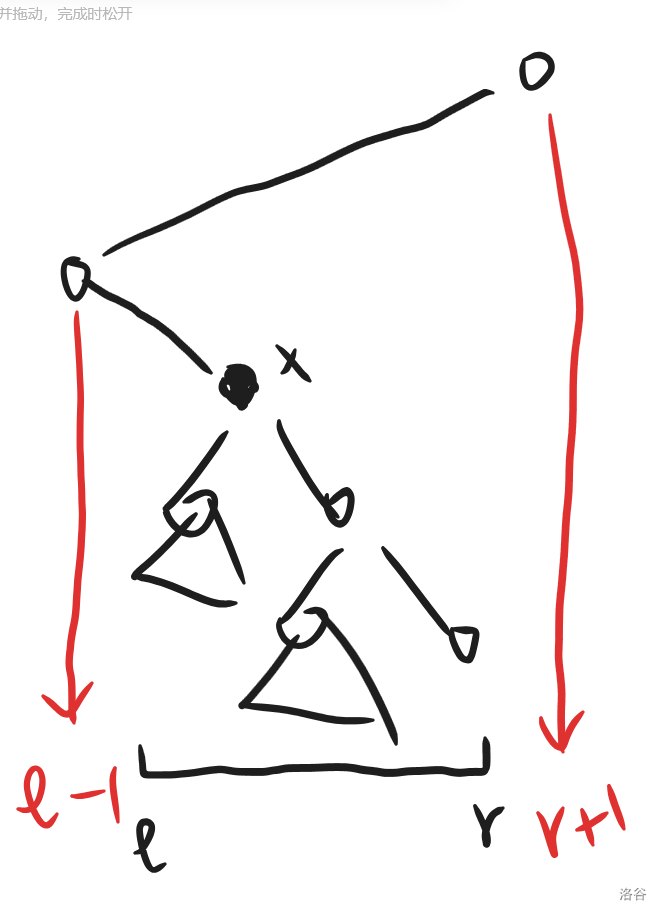
由圖可知:xxx 的權值就是 al?1×ar+1a_{l-1}\times a_{r+1}al?1?×ar+1?,不妨認為 a0=an+1=1a_0=a_{n+1}=1a0?=an+1?=1。那就可以進行區間 dp 了,設 f(l,r)f(l,r)f(l,r) 表示子樹 [l,r][l,r][l,r] 的最大權值,轉移就是
f(l,r)=al?1×ar+1+max?l≤x≤rf(l,x?1)+f(x+1,r)
f(l,r)=a_{l-1}\times a_{r+1}+\max_{l\le x\le r}f(l,x-1)+f(x+1,r)
f(l,r)=al?1?×ar+1?+l≤x≤rmax?f(l,x?1)+f(x+1,r)
時間復雜度 O(n3)O(n^3)O(n3),空間復雜度 O(n2)O(n^2)O(n2)。
為啥賽時沒推出來呢?我一直在想能不能把點從根轉化為從根到點,這樣子權值就變成最后一個滿足條件的點而非第一個,然后 balabala 就墜機了。開了一個 500×500×500×2500\times 500\times 500\times 2500×500×500×2 的數組導致 MLE 0pts。
#include <bits/stdc++.h>
bool MemoryST; using namespace std;
#define ll long long
#define mk make_pair
#define open(x) freopen(#x".in", "r", stdin), freopen(#x".out", "w", stdout)
#define lowbit(x) ((x) & (-(x)))
#define lson l, mid, rt << 1
#define rson mid + 1, r, rt << 1 | 1
#define BCNT __builtin_popcount
#define cost_time (1e3 * clock() / CLOCKS_PER_SEC) << "ms"
#define cost_space (abs(&MemoryST - &MemoryED) / 1024.0 / 1024.0) << "MB"
const int inf = 0x3f3f3f3f;
const ll linf = 1e18;
mt19937 rnd(random_device{}());
template<typename T> void chkmax(T& x, T y) { x = max(x, y); }
template<typename T> void chkmin(T& x, T y) { x = min(x, y); }
template<typename T> T abs(T x) { return (x < 0) ? -x : x; }
const int maxn = 505;
int n, a[maxn]; ll f[maxn][maxn];
bool MemoryED; int main() {scanf("%d", &n), a[0] = a[n + 1] = 1;for (int i = 1; i <= n; i ++) scanf("%d", &a[i]);for (int i = 1; i <= n; i ++) f[i][i] = 1ll * a[i - 1] * a[i + 1];for (int len = 2; len <= n; len ++)for (int l = 1, r = l + len - 1; r <= n; l ++, r ++) {for (int x = l; x <= r; x ++)chkmax(f[l][r], (x == l ? 0 : f[l][x - 1]) + (x == r ? 0 : f[x + 1][r]));f[l][r] += 1ll * a[l - 1] * a[r + 1];}printf("%lld", f[1][n]);return 0;
}
T3
給定一個長度為 nnn 的序列 aaa,QQQ 次詢問,每次給定 [l,r][l,r][l,r](保證 l<rl<rl<r),求
max?i,j∈[l,r],i≠jgcd?(ai,aj) \max_{i,j\in[l,r],i\ne j}\gcd(a_i,a_j) i,j∈[l,r],i=jmax?gcd(ai?,aj?)
n,Q≤2×105n,Q\le 2\times 10^5n,Q≤2×105。
luqyou 在前兩天的膜你賽中出了近乎一樣的題,且昨天晚上寢室的雜題選講環節中有人提到了支配點對這個東西。考慮一對 (i1,j1)(i_1,j_1)(i1?,j1?),如果有一對 (i2,j2)(i_2,j_2)(i2?,j2?) 滿足 i1≤i2<j2≤j1i_1\le i_2<j_2\le j_1i1?≤i2?<j2?≤j1? 且 gcd?(ai1,aj1)≤gcd?(ai2,aj2)\gcd(a_{i_1},a_{j_1})\le \gcd(a_{i_2},a_{j_2})gcd(ai1??,aj1??)≤gcd(ai2??,aj2??),那 (i1,j1)(i_1,j_1)(i1?,j1?) 的貢獻就不需要考慮了。也就是說,我們可以找出若干對真正對每個詢問有貢獻的點對,稱為支配點對。哪些點對是支配點對呢?考慮對于每個 ddd,我們找出所有是 ddd 的倍數的 aia_iai? 的下標序列 i1,i2??,iki_1,i_2\cdots,i_ki1?,i2??,ik?,從小到大排序后顯然只有 (i1,i2),(i2,i3),?(i_1,i_2),(i_2,i_3),\cdots(i1?,i2?),(i2?,i3?),? 這樣的點對可能是支配點對。進一步分析,對于一個 iii,假設在上一步中選出了若干個可能為支配點對的點對 (i,j1),(i,j2),??,(i,jk)(i,j_1),(i,j_2),\cdots,(i,j_k)(i,j1?),(i,j2?),?,(i,jk?) 并且 j1<j2<?<jkj_1<j_2<\cdots<j_kj1?<j2?<?<jk?;那么對于一個 ju<jvj_u<j_vju?<jv?,如果 gcd?(i,ju)≥gcd?(i,jv)\gcd(i,j_u)\ge \gcd(i,j_v)gcd(i,ju?)≥gcd(i,jv?) 那么 (i,jv)(i,j_v)(i,jv?) 這對點對也沒有用了。這樣最終的點對數量大概是所有 aia_iai? 的因子個數和,但顯然遠遠不到,大概可以估成 O(nlog?n)O(n\log n)O(nlogn)。最后做一個二維數點即可。
#include <bits/stdc++.h>
using namespace std;
const int maxn = 2e5 + 5, V = 2e5;
int n, Q, a[maxn]; vector<int> tab[maxn];
vector<int> f[maxn]; vector<pair<int, int> > imp[maxn];
#define lowbit(x) ((x) & (-(x)))
struct Point {int x, y, val, qid;
}; vector<Point> p;
int b[maxn], ans[maxn];
void add(int x, int v) { x = n - x + 1;for (; x <= n; x += lowbit(x))b[x] = max(b[x], v);
} int ask(int x) { x = n - x + 1;int res = 0;for (; x; x -= lowbit(x))res = max(res, b[x]);return res;
}
#define open(x) freopen(#x".in", "r", stdin), freopen(#x".out", "w", stdout)
int read() {char c = getchar();for (; c < '0' || c > '9'; c = getchar());int s = 0;for (; c >= '0' && c <= '9'; c = getchar())s = (s << 1) + (s << 3) + (c ^ 48);return s;
}
int main() { // open(data);n = read();for (int i = 1; i <= n; i ++)a[i] = read(), tab[a[i]].push_back(i);for (int i = 2; i <= V; i ++)for (int j = i; j <= V; j += i)if (!tab[j].empty())for (int k : tab[j]) f[i].push_back(k);for (int i = 2; i <= V; i ++) if ((int)f[i].size() > 1) {int len = (int)f[i].size(); sort(f[i].begin(), f[i].end());for (int j = 0; j < len - 1; j ++) {int now = f[i][j], nxt = f[i][j + 1];while (!imp[now].empty() && imp[now].back().second >= nxt) imp[now].pop_back();imp[now].emplace_back(i, nxt);}} for (int i = 1; i <= n; i ++)for (auto j : imp[i]) p.push_back(Point { j.second, i, j.first, 0 });Q = read();for (int i = 1, L, R; i <= Q; i ++) L = read(), R = read(), p.push_back(Point { R, L, 0, i });sort(p.begin(), p.end(), [&](const Point &x, const Point &y) {return x.x == y.x ? y.qid > 0 : x.x < y.x;}); for (Point cur : p) {int x = cur.x, y = cur.y, val = cur.val, qid = cur.qid;if (qid != 0) ans[qid] = max(1, ask(y));else add(y, val);} for (int i = 1; i <= Q; i ++)printf("%d\n", ans[i]);return 0;
}
唯一一道做對的題
T4
給定一個樹,初始只有一個根節點 111,QQQ 次操作,要么給定一個點 xxx 和一個 www,在 xxx 節點的孩子中增加一個點,邊權為 www;要么給定 u,vu,vu,v,求對于所有 vvv 子樹中的點 iii,uuu 到 iii 的路徑的邊權異或和的最大值。
1≤Q≤2×1051\le Q\le 2\times 10^51≤Q≤2×105,0≤w≤2300\le w\le 2^{30}0≤w≤230。
把操作離線下來得到一棵 nnn 個點的樹。考慮 u,vu,vu,v 兩點間路徑異或和就等于 uuu 到根的路徑異或和異或上 vvv 到根的路徑異或和,那操作就變成:
- 給一個點一個點權;
- 給定一個 www 和點 uuu,求 uuu 的子樹中所有點權異或上 www 的最大值。
不妨在這棵樹上 dfs,每個點維護一個子樹中所有點權的 01Trie,每次像線段樹合并那樣合并孩子的 01Trie;01 Trie 上對每條邊維護一個最早建立時間即可。時間復雜度 O(nlog?n)O(n\log n)O(nlogn)。
賽時做法因為空間爆了只能拿 70pts,好像也能進行類似的離線使空間復雜度下降。
#include <bits/stdc++.h>
bool MemoryST; using namespace std;
#define ll long long
#define mk make_pair
#define open(x) freopen(#x".in", "r", stdin), freopen(#x".out", "w", stdout)
#define lowbit(x) ((x) & (-(x)))
#define lson l, mid, rt << 1
#define rson mid + 1, r, rt << 1 | 1
#define BCNT __builtin_popcount
#define cost_time (1e3 * clock() / CLOCKS_PER_SEC) << "ms"
#define cost_space (abs(&MemoryST - &MemoryED) / 1024.0 / 1024.0) << "MB"
const int inf = 0x3f3f3f3f;
const ll linf = 1e18;
mt19937 rnd(random_device{}());
template<typename T> void chkmax(T& x, T y) { x = max(x, y); }
template<typename T> void chkmin(T& x, T y) { x = min(x, y); }
template<typename T> T abs(T x) { return (x < 0) ? -x : x; }
const int maxn = 2e5 + 5;
int Q, tim[maxn], f[maxn], n; vector<pair<int, int> > que[maxn];
namespace Graph {struct Edge { int to, nxt; } e[maxn << 1];int head[maxn], ecnt;void addEdge(int u, int v) { e[++ ecnt] = Edge { v, head[u] }, head[u] = ecnt; }
} using namespace Graph; char tmp[10];
struct Trie {Trie *son[2]; int create_time;Trie(int t0 = inf) { son[0] = son[1] = nullptr, create_time = t0; }
} *root[maxn];
void insert(Trie *rt, int x, int tim) {Trie *cur = rt;for (int i = 29; ~i; i --)if (x & (1 << i)) {if (cur -> son[1] == nullptr)cur -> son[1] = new Trie();chkmin(cur -> son[1] -> create_time, tim), cur = cur -> son[1];} else {if (cur -> son[0] == nullptr)cur -> son[0] = new Trie();chkmin(cur -> son[0] -> create_time, tim), cur = cur -> son[0];}
} int query(Trie *rt, int x, int tim) {Trie *cur = rt; int ans = 0;for (int i = 29; ~i; i --) if (x & (1 << i)) {if (cur -> son[0] != nullptr && cur -> son[0] -> create_time < tim)ans += (1 << i), cur = cur -> son[0];else cur = cur -> son[1];} else {if (cur -> son[1] != nullptr && cur -> son[1] -> create_time < tim)ans += (1 << i), cur = cur -> son[1];else cur = cur -> son[0];}return ans;
} Trie *merge(Trie *rt, Trie *oth) {if (rt == nullptr) return oth;if (oth == nullptr) return rt;chkmin(rt -> create_time, oth -> create_time);rt -> son[0] = merge(rt -> son[0], oth -> son[0]), rt -> son[1] = merge(rt -> son[1], oth -> son[1]);delete oth; oth = nullptr; return rt;
} int ans[maxn]; void dfs(int u, int fa) {root[u] = new Trie(0); insert(root[u], f[u], tim[u]);for (int i = head[u], v; i; i = e[i].nxt) {if ((v = e[i].to) == fa) continue;dfs(v, u), root[u] = merge(root[u], root[v]);} for (auto [tim, val] : que[u])ans[tim] = query(root[u], val, tim);
} vector<int> qid;
bool MemoryED; int main() {scanf("%d", &Q); int n = 1; tim[1] = f[1] = 0;for (int i = 1, u, v, w; i <= Q; i ++) {scanf("%s", tmp);if (tmp[0] == 'A') {scanf("%d %d", &u, &w), tim[++ n] = i;f[n] = f[u] ^ w, addEdge(n, u), addEdge(u, n);} else scanf("%d %d", &u, &v), que[v].emplace_back(i, f[u]), qid.push_back(i);} dfs(1, 0); for (int i : qid) printf("%d\n", ans[i]);return 0;
}
還是非常好寫的。

 的核心介紹與使用教程)
)
)

集合類詳解)
 等待事件(1)-概述)

)










