1. 邏輯回歸

1.1. 線性回歸 vs 邏輯回歸

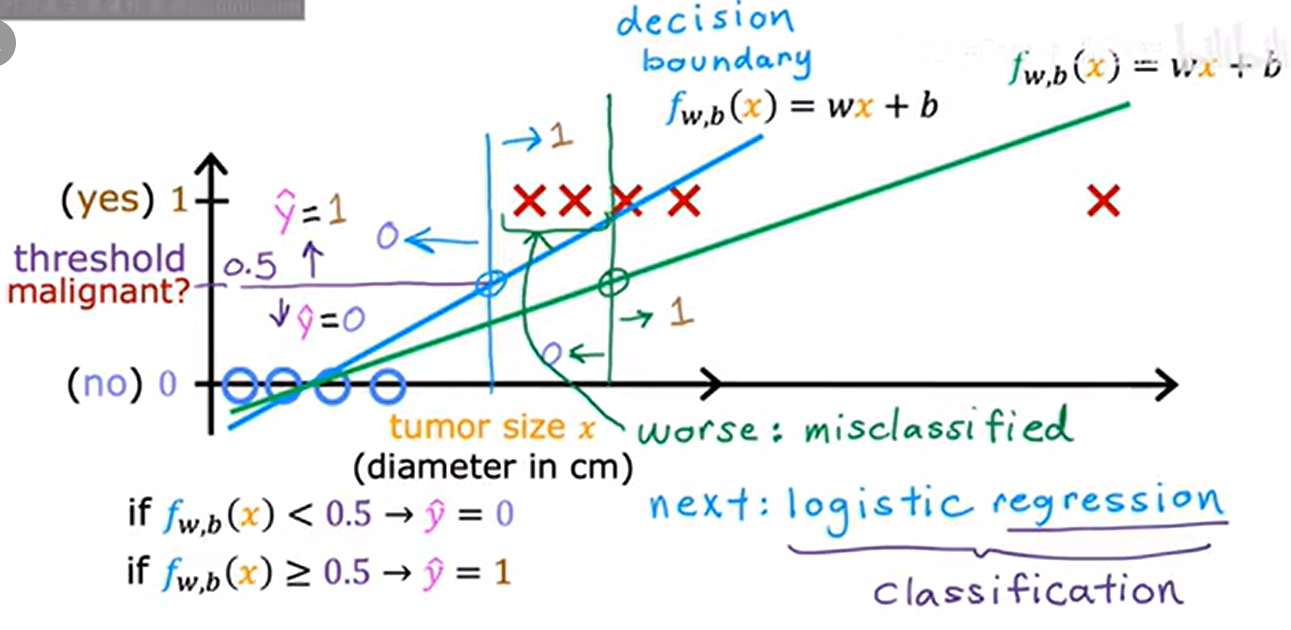
1.2. 場景：腫瘤分類

• X軸：腫瘤大小；Y軸：0-良性，-惡性
• 決策邊界（decision boundary：由線性函數 (f_{w,b}(x) = wx + b) 定義，用于劃分兩個類別
  • 決策邊界及左邊：0-良性，右邊：1-惡性

在右邊添加額外訓練樣本（腫瘤很大的樣本）會導致線性函數發生偏移

• （藍）線性函數變成（綠）線性函數；
• 決策邊界也右移
  • 原本為惡性的腫瘤樣本預測為0-良性
  • 顯然錯誤，右邊的樣本不應該影響怎么分類良惡性的
  • 添加新的樣本，線性函數更差

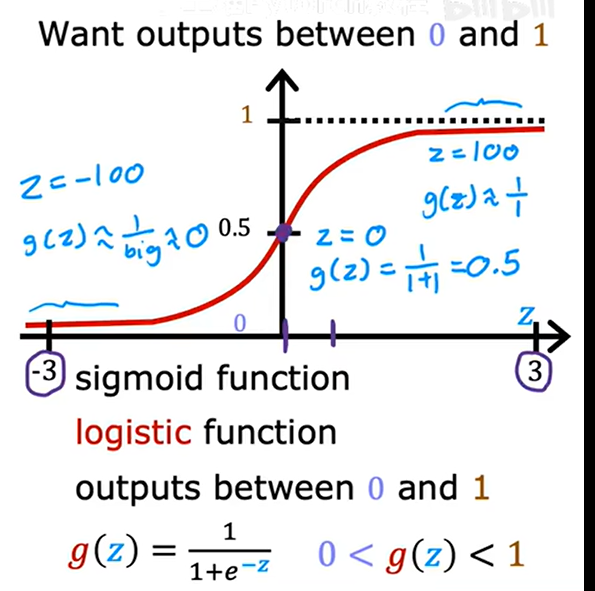
1.3. 邏輯函數

Logistic Function，也稱為 Sigmoid 函數，S 形曲線函數。它將任意實數輸入值映射到區間 (0, 1)。

g(x) =1/（1 + e^（-x）)

• e 是自然常數（約等于 2.71828）

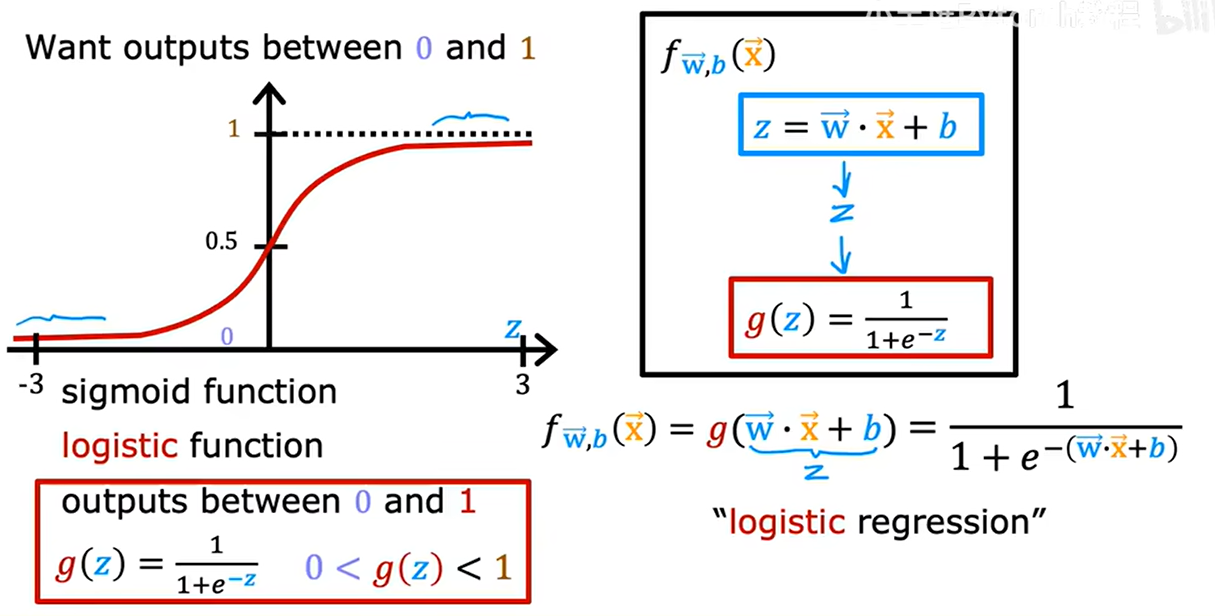
1.4. 構建邏輯回歸算法

輸入一個特征/一組特征x，輸出一個(0，1)間的數字

1. 定義z值：z= wx + b
2. z值作為輸入，帶入到邏輯函數 g(z) =1/（1 + e^（-z）) 中
3. 得到邏輯回歸模型 f(x)=g(wx+b)

輸出的理解：對于給定輸入x值時，類別y=1的概率

• 腫瘤大小為x時，腫瘤為惡性的概率

2. 決策邊界

z= wx + b ----> g(z) =1/（1 + e^（-z）) ------> f(x)=g(wx+b)

1. f(x)>0.5時，表分類=1概率>0.5，分類=1；否則f(x)<0.5時，表分類=1概率<0.5，分類=0
2. f(x)>0.5時，根據邏輯函數曲線圖，z>0，z=wx+b
3. wx+b>0時，z>0，f(x)>0.5，分類=1；wx+b<0時，z<0，f(x)<0.5，分類=0
4. 決策邊界：wx+b=0的線

有兩個輸入特征：x1、x2

• z=w1x1+w2x2+b
• f(x)=g(w1x1+w2x2+b)
• 決策邊界：w1x1+w2x2+b=0

令w1=w2=1，b=-3

• z=x1+x2-3
• 決策邊界：x1+x2=3

  

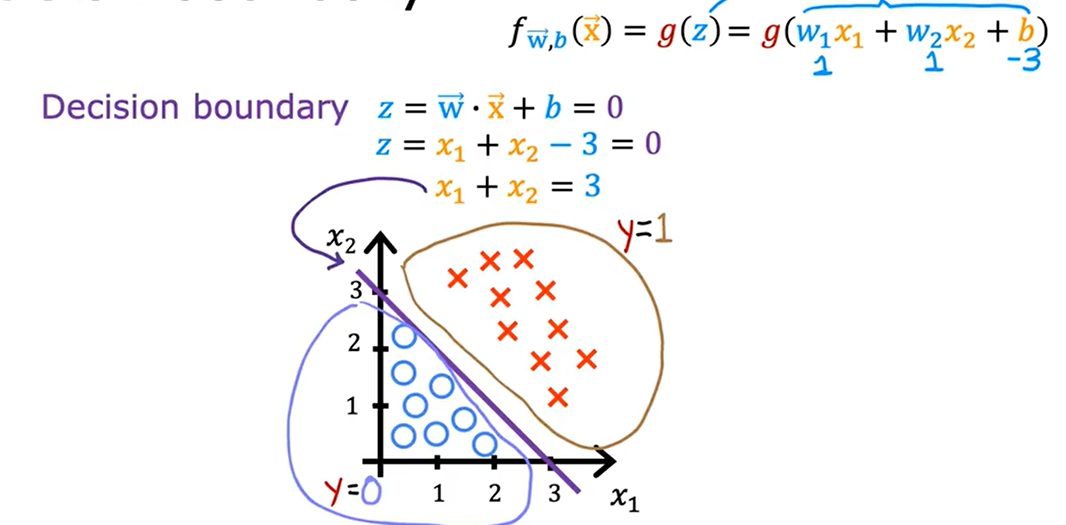
決策邊界非直線

• 多項式特征：z=w1x1^2+w2x2^2+b
• 假設w1=w2=1,b=-1；z=x1^2+x2^2-1
• 決策邊界：x1^2+x2^2=1
  • 圓外：z>0,f(z)>0.5,分類y=1
  • 圓內：z<0,f(z)<0.5,分類y=0

更復雜的決策邊界

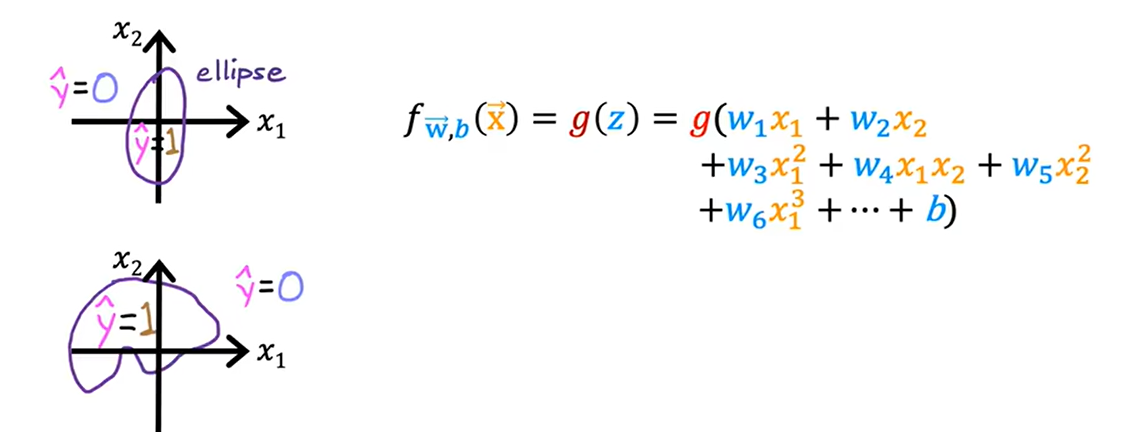
3. 邏輯回歸的代價函數

代價函數提供一種衡量特定參數集對訓練數據擬合程度的方法，幫助選擇更好的參數

平方誤差代價函數（1/2在求和符號外面時）

• 得到非凸代價函數：使用梯度下降，會有很多局部最小值

損失函數：單個訓練的損失

• y^(i)真實值，f(x^(i))預測值
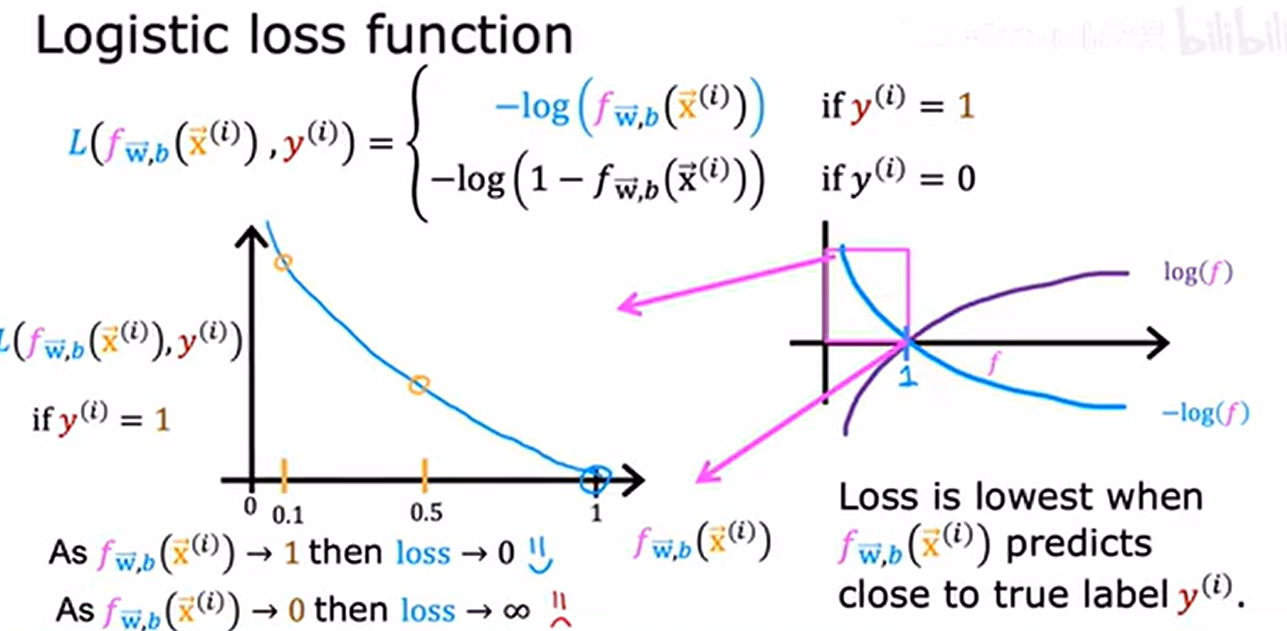
• 橫軸：f，即標簽y=1的概率預測值；縱軸：L，即損失函數

當 y^(i) = 1 時的損失函數曲線：

• 當 f(x^(i))->1（預測正確），損失 L -> 0；
• 當 f(x^(i))->0（預測錯誤），損失 L -> +∞

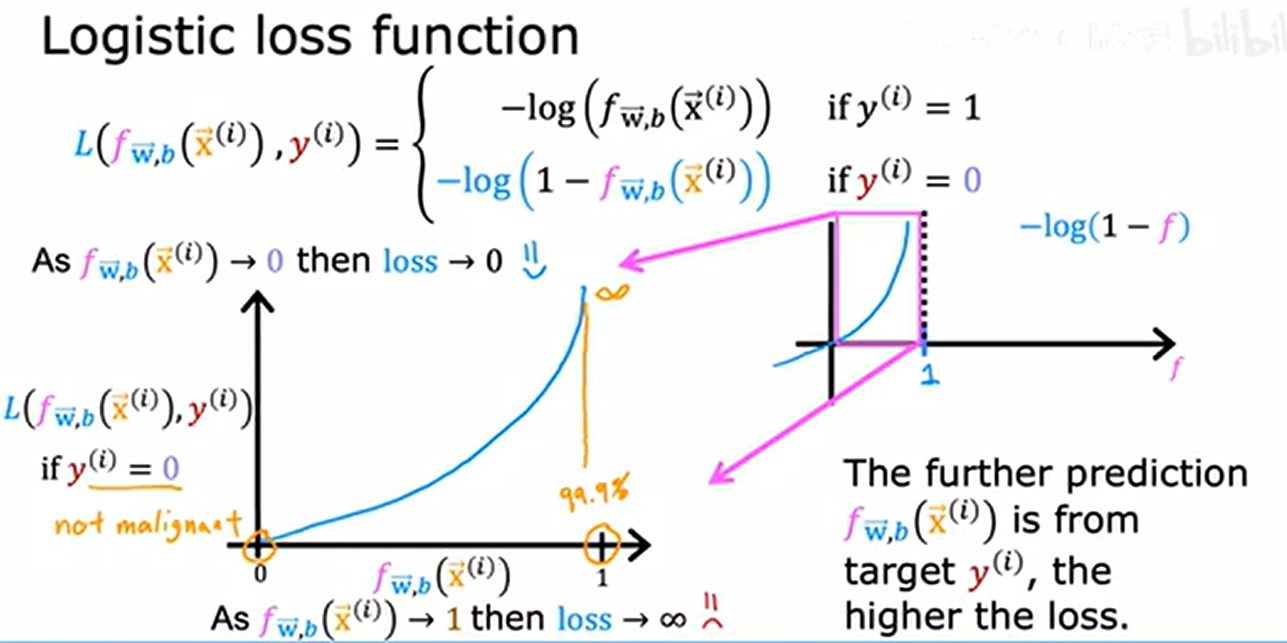
當 y^(i) = 0 時的損失函數曲線：

• 當 f(x^(i))->0（預測正確），損失 L -> 0；
• 當 f(x^(i))->1（預測錯誤），損失 L -> +∞

代價函數

4. 邏輯回歸的簡化版代價函數

5. 梯度下降的實現

如何選擇w1、w2、w3、...、b的值使代價函數值盡可能小

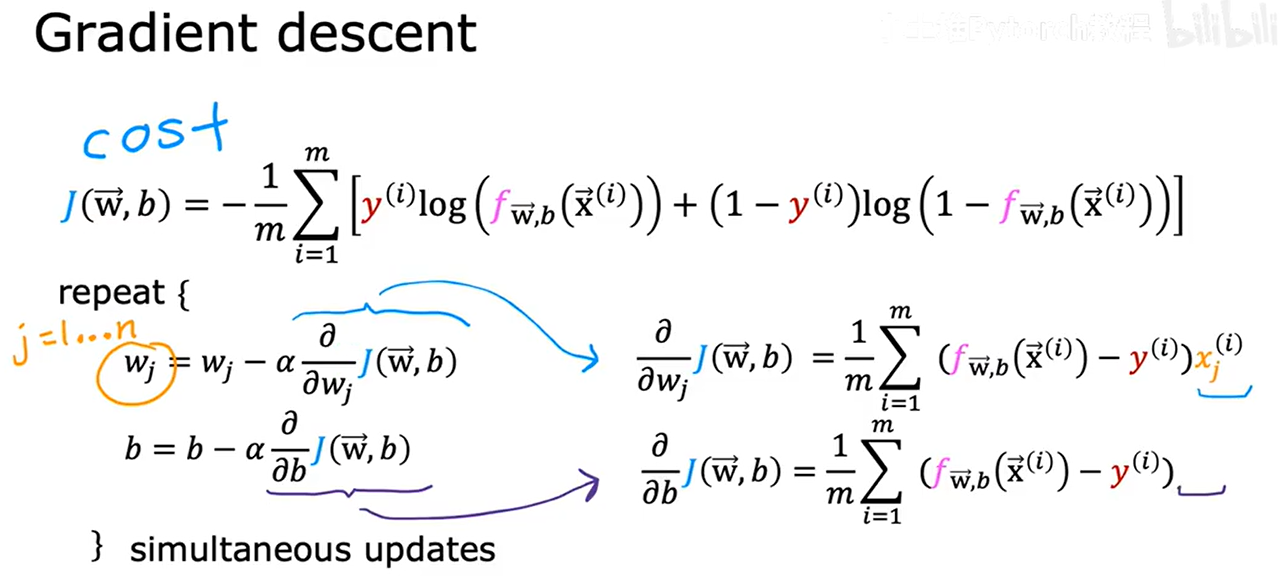
對于repeat，先計算兩個式子的右側，再同時更新到左側

• 線性回歸：預測函數為 f(x) = wx + b
• 邏輯回歸：預測函數為 f(x) = 1/(1 + e^(-(wx + b)))（sigmoid 函數）

更新公式形式與線性回歸的相同，但f(x)定義不同

1. 監督梯度下降
2. 向量化
3. 特征縮放

6. 過擬合問題

過擬合（Overfitting）：模型在訓練數據上表現良好，但在新的、未見過的數據上表現不佳，高方差（High Variance）

欠擬合（Underfitting）：模型的復雜度較低，無法捕捉到數據中的關鍵特征和潛在規律，模型在訓練、測試數據上的表現都很差，高偏差（High Bias）

泛化（Generalization） 是指模型在未見過的新數據上表現良好的能力。

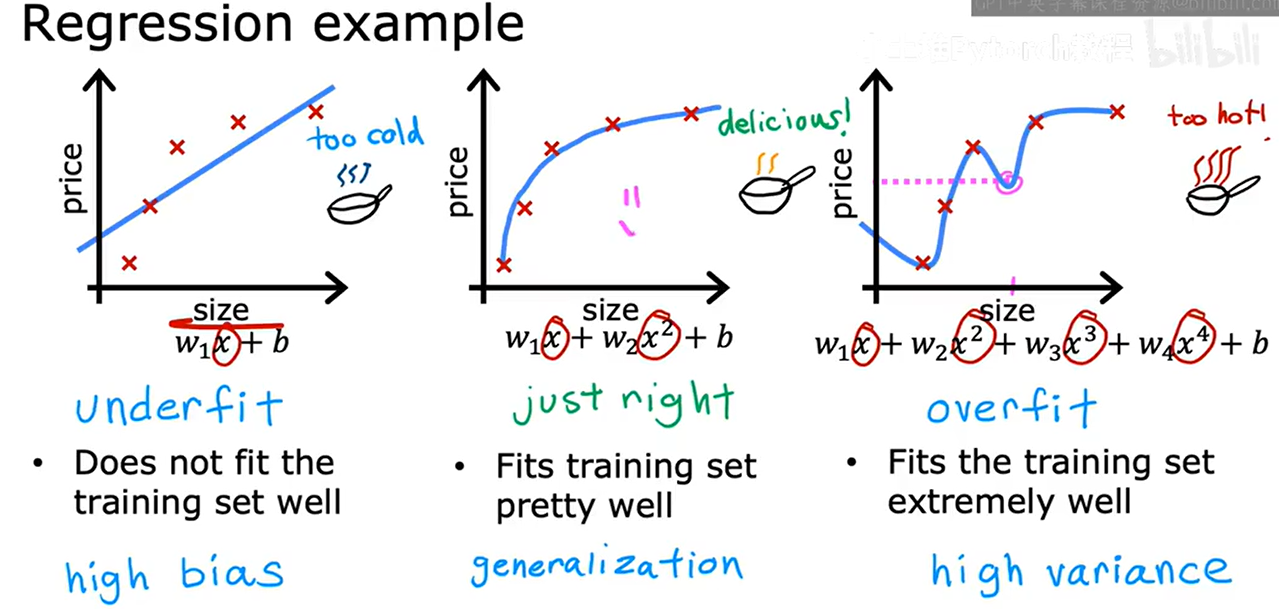
過擬合也適用于分類

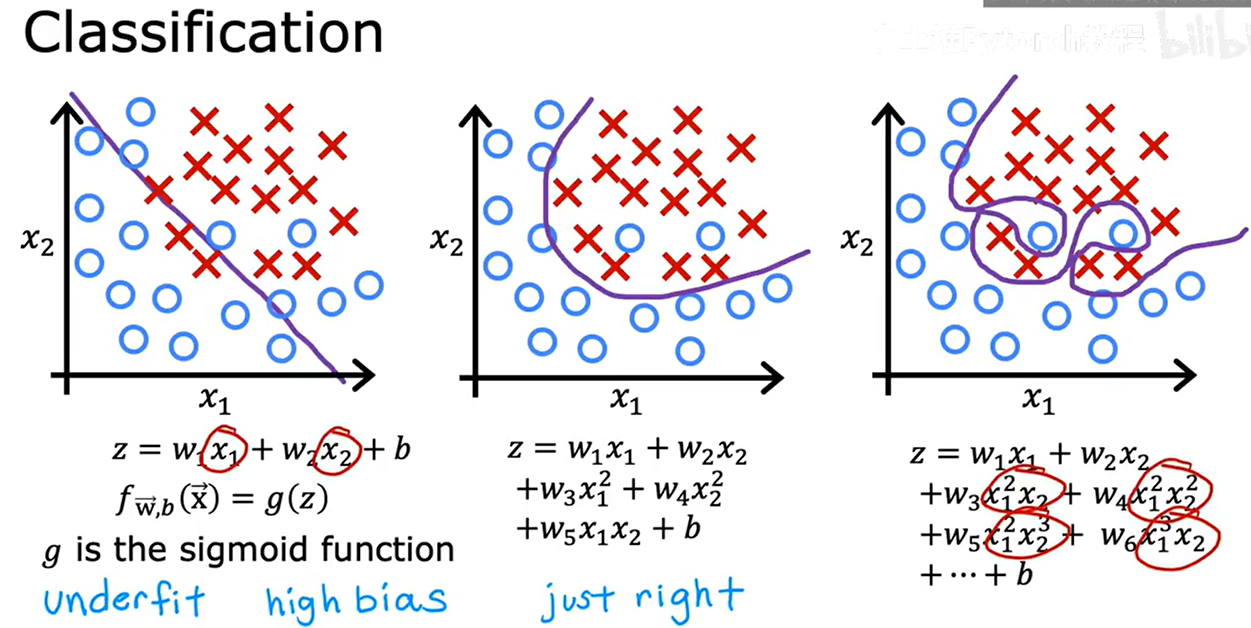
7. 解決過擬合

1. 獲得更多數據
2. 嘗試選擇、使用特征的子集
3. 正則化減小參數大小🔺

8. 帶正則化的成本函數

模型過擬合的本質是參數值過大（如高次多項式的系數），導致模型對訓練數據的微小波動過度敏感。正則化通過在代價函數中引入參數懲罰項，迫使參數值 “收縮” 到較小范圍，從而：

• 降低模型復雜度（避免過度復雜的決策邊界）；
• 增強模型對新數據的泛化能力。

正則化：對特征的參數w_j懲罰，對b不操作

1. L2正則化：溫和收縮參數，保留所有特征
   1. 所有參數 w_j 都會被 “拉向 0”，但不會嚴格為 0（系數值變小但非零）。
   2. 傾向于讓參數值更平均（避免某一特征權重過大），使模型更 “平滑”。
2. L1正則化：稀疏化參數，實現自動特征選擇
   1. 部分參數 w_j 會被直接壓縮至 0（“稀疏化”），相當于自動實現 “特征選擇”。
   2. 能篩選出對目標影響最大的核心特征，剔除冗余特征。

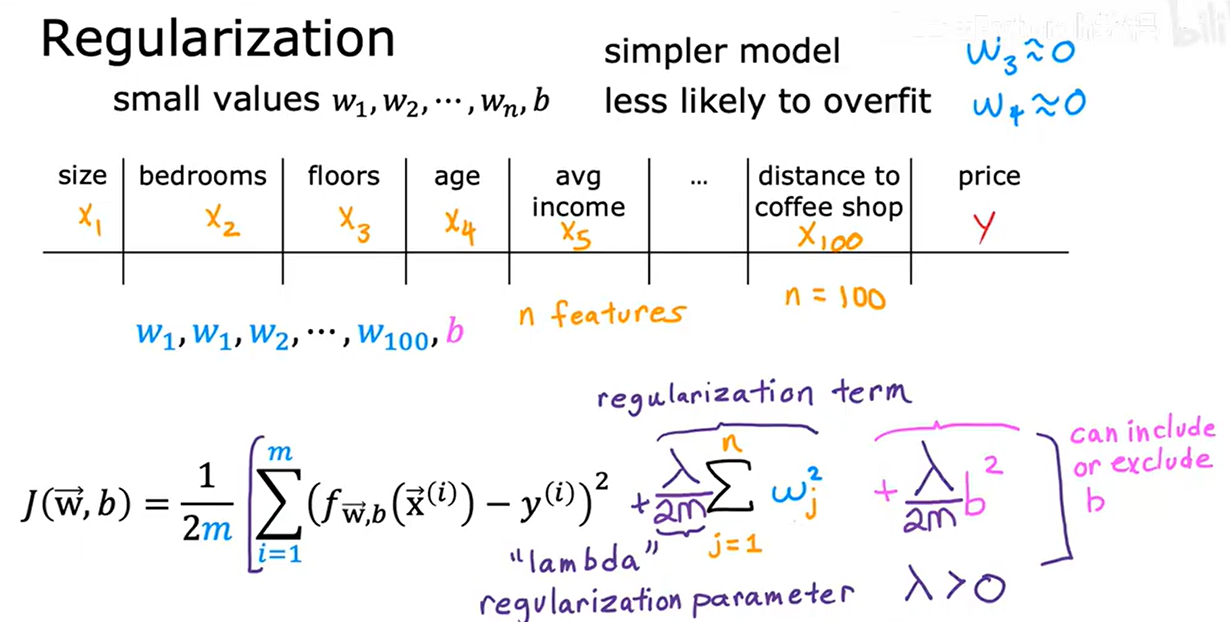
正則化參數 ?

• =0：無正則化，模型可能過擬合（完全擬合訓練數據）。
• ? 非常大：正則化權重大，所有參數 w1...wj 被壓縮至 0，模型復雜度降低 f(x)~=b（可能欠擬合）。
• 選擇原則：通過交叉驗證（如網格搜索）找到最優 ?，使驗證集上的模型性能（如準確率、損失值）最優。

9. 正則化線性回歸

和線性回歸相比，repeat部分對 b 的更新沒變化，符合正則化試圖縮小參數 wi ，不改變 b

正則化在每次迭代的作用：更新wj時，先?一個略小于1的數，稍微縮小wj值，再減去

• 第一部分：w_j*(1-ɑ*?/m) 是正則化項，確保權重不會無限制增長。
• 第二部分：是標準的梯度下降更新項，用于最小化預測誤差。

10. 正則化邏輯回歸

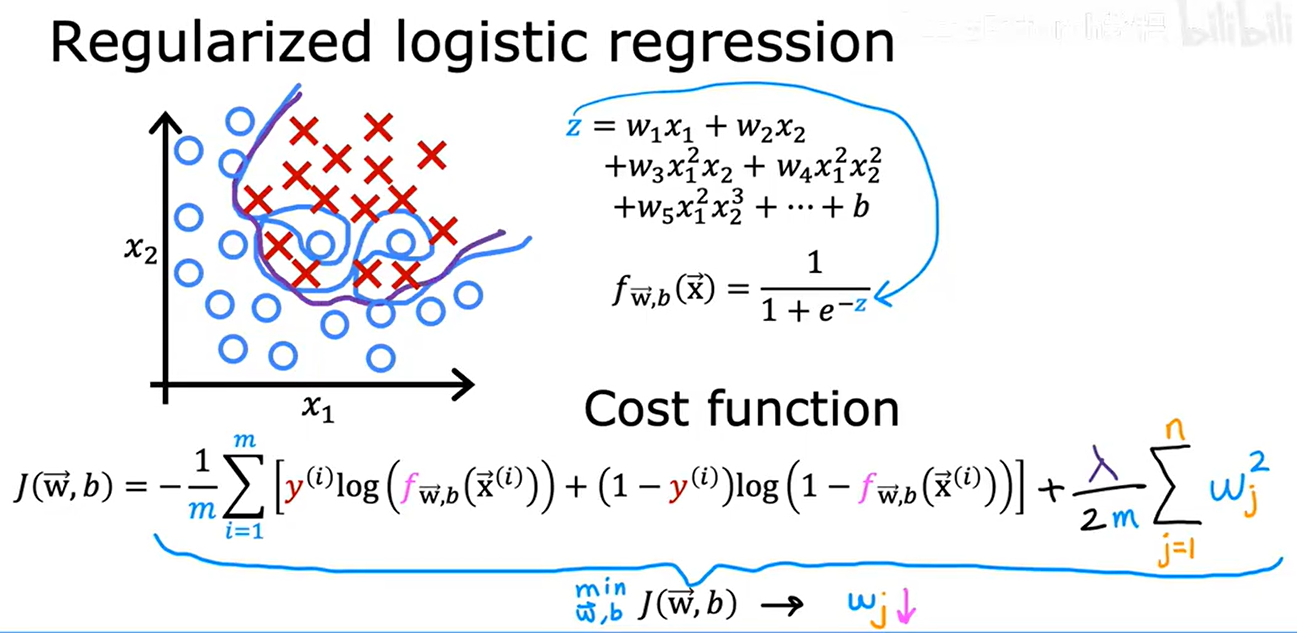
對于梯度下降迭代最小化代價函數，repeat和正則化線性回歸相同，只是各自的 f(x) 函數表達式不同