前言
實話說,過去一兩月一直忙著我司兩大類項目的推進
- 一類是正在逐一上線基于大模型的論文翻譯、論文審稿、論文對話、論文修訂/潤色、論文idea提煉等等(截止到24年8月底,其中的審稿和翻譯已上線七月官網?)
- 一類是正在抓緊做面向一個個工廠的具身智能機器人的解決方案,且很快會分別在我司在各地的辦公室(南京、長沙、武漢、北京),一一擺上一兩臺干活的具身機器人
所以雖然說mamba2已發布一月有余,但實在是沒有一塊完整的時間來對其做詳盡而細致的解讀,而最終促使我來寫的最大的動力還是來源于我半年前對mamba1的解讀,實在是太受歡迎了且影響力巨大(截止到24年7月初,半年下來閱讀量10萬,2千余次收藏,在同樣發表半年內文章中的表現很突出)
加之之前就有讀者在我對上面mamba1做解讀的文章下留言,什么時候出mamba2的解讀,讓我好幾次躍躍欲試想開寫
然,在我下定決心寫本文之前,內心還是有過一陣小糾結的
- 一方面,怕沒有一大塊完整的時間(回想過去,23年上半年因為ChatGPT,公司重新煥發生機,個人也前所未有的沉迷于技術,又因23年下半年做大模型項目延續至今,今后因為業務的增長 大量的各種會議 可能難以再像過去一年半百分百沉迷于技術了)
- 二方面,mamba2的論文特別長,即《Transformers are SSMs: Generalized Models and Efficient Algorithms Through Structured State Space Duality》一文長達52頁(這個則是兩位作者寫的解讀blog:State Space Duality (Mamba-2) Part I - The Model),全是各種概念、公式,故為了更好的理解mamba2,建議先熟練mamba1
當然,mamba2的核心主要解決兩個問題:1 打通SSM與transformer之間的聯系,2 將mamba2表述為矩陣乘法以加速訓練
具體而言,在結構化掩碼注意力SMA中
1) 首先,可以通過掩碼矩陣(比如因果掩碼)來指導注意力機制——控制信息流向,從而決定哪些信息是重要的,哪些可以忽略
2) 其次,針對傳統注意力機制下的計算對Q, K, V的操作——L* (QK^T)V,都可以找到一個近似Q K V的結構化的N-半可分矩陣,然后,通過與對應的N-半可分矩陣相乘,以達到加速計算的目的
總之,這種矩陣能夠表示不同種類的注意力形式,相當于都能通過矩陣運算來進行不同掩碼下的注意力操作
3) 而N-半可分矩陣「準確的說是1-半可分矩陣(簡稱1-SS矩陣)」,可以直接應用于SSM中的A矩陣(表示狀態轉移的矩陣)
從而通過將SMA中的結構化矩陣應用于SSM中的A矩陣,如此,便將SSM和注意力結合起來了
不過還是因為過去十多年寫博客的經驗,使得自己在面對再難啃的算法都有足夠的自信與底氣,堅信都可以一步步拆解、一步步抽絲剝繭并清晰易懂的寫出來
- 讀者在看本文時,也不用急,一步步來,可以慢慢看懂的,且未來一兩月 我也會不斷修訂本文以讓之不斷更加通俗易懂
- 且為了解釋清楚每一個定義、公式、矩陣,我會在文中不厭其煩的、不斷列舉大量、具體,但論文中沒有的矩陣示例,以不斷降低理解門檻
故本文最終還是來了
第一部分 背景回顧:從SSM、結構化矩陣到SSD的一系列定義
1.1 結構化SSM的定義:Structured State Space Model
1.1.1 離散化、循環結構表示、卷積結構表示
雖然在之前對mamba1的講解中已經講過了很多背景,但為本文的完整性起見,還是把一系列背景知識按照mamba2論文的思路,再度逐一梳理下
首先,結構化狀態空間序列模型S4是受到的特定連續系統的啟發(如下述公式1所示,是結構化SSM的一般離散形式),該系統將一維序列通過隱式潛在狀態
?做映射(相當于將SSM簡單地寫成矩陣乘法)

- 其中
、
均是標量,
則被視為具有N維的向量,且
- 其中的
?矩陣?控制時間動態,從而必須是結構化的(結構化SSM也因此得名),以便能夠足夠高效地計算這種序列到序列的轉換,從而在深度神經網絡中使用
梳理一下結構化SSM的發展歷史
- 最初的結構化SSM起源于函數
的連續時間映射,而不是直接對序列進行操作
在連續時間視角中,在公式(1a)中,矩陣 (𝐴, 𝐵)不是直接學習的,而是從底層參數 生成的,并且伴隨著一個參數化的步長 Δ
生成的,并且伴隨著一個參數化的步長 Δ
“連續參數” 通過固定公式
通過固定公式 和
和 轉換為“離散參數”(𝐴, 𝐵),其中這對 (
轉換為“離散參數”(𝐴, 𝐵),其中這對 (,
)被稱為discretization rule
- 結構化 SSM 可以被視為一種遞歸神經網絡RNN,其中線性賦予它們額外的屬性,并使它們能夠避免傳統 RNN 的順序計算。相反,盡管有這種簡化,SSM 仍然可以完全表達為序列變換
更多詳見此文《一文通透想顛覆Transformer的Mamba:從SSM、HiPPO、S4到Mamba》的第2.1.2節
- 當SSM的動態在時間上是恒定的,如公式(1)所示,該模型稱為線性時不變(linear time-invariant,簡稱LTI)模型,在這種情況下,它們等同于卷積
因此,SSM也可以被視為CNN的一種類型,但卷積核通過SSM參數 (𝐴, 𝐵, 𝐶)隱式參數化,且卷積核通常是全局的而不是局部的
反過來,通過經典的信號處理理論,所有充分良好的卷積都可以表示為SSM
通常,以前的LTI SSM會

- 使用卷積模式進行高效的可并行訓練(整個輸入序列提前看到)
- 并切換到遞歸模式(如本節開頭的公式1所述)進行高效的自回歸推理(輸入逐步看到)
1.1.2 mamba一代的問題:沒法用矩陣乘法
當在 Mamba1 中被引入為選擇性 SSM時,則相當于允許(A, B, C)這三個參數隨時間而變化(如下面公式2所示),此時,、
、
公式2與標準的 LTI 公式1相比,該模型可以在每個時間步選擇性地關注或忽略輸入

在信息密集型數據如語言上,它的表現被證明遠優于 LTI SSM,特別是隨著其狀態大小 N的增加,允許更多的信息容量
然而,它只能在遞歸模式下計算,而不是卷積模式,并且需要“專門的硬件感知實現”才能高效,即如下圖所示

即便如此,它仍然不如硬件友好的模型(如 CNN 和 Transformer)高效,因為它沒有利用矩陣乘法單元,而現代加速器(如 GPU 和 TPU)正是為此而專門設計的
總之,雖然時間不變SSM 與連續、遞歸和卷積序列模型密切相關,但它們與注意力機制沒有直接關系。所以mamba2想揭示選擇性SSM和注意力機制之間的更深層次關系,并利用這一點顯著提高SSM的訓練速度,同時允許更大的狀態規模N
1.1.3?結構化SSM作為序列變換:三個定義之2.1 2.2 2.3
請直接看一下三個定義(分別定義序列變換、S6和注意力機制的序列變換形式、序列變換與矩陣的聯系)
- 定義 2.1?一般而言,所謂序列變換指的是序列上的參數化映射
其中,,并且𝜃是任意參數集合
表示序列或時間軸,可以作為下標索引到第一個維度,例如
序列變換(例如SSM或自注意力機制)是深度序列模型的基石,它們被整合到神經網絡架構中 例如Transformer
其實上面的公式1或2中的SSM便是一個序列變換,且 P = 1
當然,它可以通過簡單地在此維度上來推廣到 P > 1(換句話說,將輸入視為 P 個獨立序列并對每個序列應用SSM,即可以將 P視為一個頭維度)
- 定義 2.2?定義SSM 操作符
作為序列變換
,由上面的公式2定義

在 SSM 中, N維度是一個稱為狀態大小或狀態維度的自由參數,也稱之為狀態擴展因子,因為它將輸入/輸出的大小擴展了 𝑁倍,這對這些模型的計算效率有影響
(其實許多類型的序列變換,例如注意力機制,都可以表示為跨序列維度的單一矩陣乘法) - 定義 2.3?如果一個序列變換
可以寫成形式
,其中
是一個依賴于參數𝜃的矩陣,稱其為矩陣變換,且用矩陣𝑀來表示序列變換

當然,在上下文明確時,通常省略對的依賴
1.2 一系列定義:注意力機制、結構化矩陣、SSD
1.2.1 線性注意力機制的定義
注意力機制已經非常經典了(如果還不熟悉注意力機制的,請參見此文:Transformer通俗筆記:從Word2Vec、Seq2Seq逐步理解到GPT、BERT),屢見不鮮,其為序列中每對位置分配分數,使每個元素能夠“關注”其余部分
迄今為止,最常見和最重要的注意力機制變體是softmax自注意力機制,其定義如下
對于,由于注意力機制需要一次次計算兩兩token之間的注意力(畢竟有這個計算
),導致了二次方的計算復雜度
為了降低二次方的復雜度,已經提出了許多注意力的變體,其中最重要的變體是線性注意力(詳見此文的2.2.1 什么是線性transformer:Transformers are RNNs與cosformer)
- 粗略地說,這類方法通過將softmax折疊到核特征映射中,并利用矩陣乘法的結合性將注意力計算中的矩陣左乘改成右乘,即
- 如下圖右側所示,將QKV的左乘變成右乘后,從?將理論計算復雜度降為線性「更多詳見此文《七月論文審稿GPT第1版:通過3萬多篇paper和10多萬的review數據微調RWKV》的2.2節」

值得一提的是
- 提出線性注意力的這個標題:
Transformers are RNNs: Fast Autoregressive Transformers with Linear Attention「作者:A Katharopoulos · 2020」 - 是否與提出mamba2的論文標題:
Transformers are SSMs: Generalized Models and Efficient Algorithms Through Structured State Space Duality
有著很高的相似性呢
再進一步,既然transformer是RNN,而SSM某種意義上也是RNN,那mamba2和transformer是否有著直接的聯系?不急,請繼續看下文的講解
- 此外,在因果(自回歸)注意力的重要情況下,他們表明,當因果掩碼被合并到左側作為
,其中
是下三角1矩陣時,右側可以擴展為遞歸(Moreover, in the important case of causal (autoregressive) attention, they show that when the causal mask is incorporated into the left-hand side as (𝐿 ? 𝑄𝐾?) · 𝑉 , where 𝐿 is the lower-triangular 1’s matrix, then the right-hand side can be expanded as a recurrence)
這個的作用在于確保在計算注意力權重時,每個位置只能看到它之前的位置(類似GPT做預訓練預測下一個token時,必會遮住當前token的后續token,不然就無所謂預測了)
- 最近的一些工作,如RetNet(Y. Sun等,2023)和GateLoop(Katsch 2023)將其加強為更一般形式的
為了方便大家更好的理解上面這段話,我再給大家舉個具體的矩陣例子,以形象說明
- 定義查詢Q、鍵K、值V矩陣,為了簡化,可以使用隨機的矩陣值來表示它們
- 接下來,計算
- 現在,我們定義一個下三角1矩陣?
,用于實現因果掩碼
- 接下來,計算
- 最后,再計算
1.2.2 結構化矩陣(Structured Matrices)的定義:方便做矩陣乘法
一般矩陣需要
個參數來表示,并且執行諸如矩陣-向量乘法等基本操作需要
時間。而所謂的結構化矩陣是指那些
- 可以壓縮表示,比如在亞二次(理想情況下是線性)參數中表示
- 并且通過快速算法(最重要的是矩陣乘法),直接操作這種壓縮表示
也許最典型的結構化矩陣家族是稀疏矩陣和低秩矩陣。 然而,還存在許多其他家族,例如Toeplitz矩陣、Cauchy矩陣、Vandermonde矩陣和蝶形矩陣
1.2.3?SSD(結構化狀態空間對偶)的定義:注意力矩陣乘以掩碼矩陣
狀態空間對偶(SSD)層可以定義為選擇性SSM(如之前公式2所示)的特例
可以應用SSM作為遞歸(或并行掃描)的標準計算,其在序列長度上具有線性復雜度。 與Mamba中使用的版本相比,SSD有兩個小的不同點:
的結構從對角線進一步簡化為標量乘以單位矩陣結構。 在這種情況下,每個
也可以僅用一個標量來表示
- 使用了更大的頭維度
,相比于Mamba1中使用的 P = 1,通常選擇
,而Transformer一般也會這樣設置頭的維度
與原始選擇性SSM相比,這些變化可以被視為在略微降低表達能力的同時 顯著提高訓練效率。 特別是,新算法將允許在現代加速器上使用矩陣乘法單元
如下圖所示

- 原論文Sec.3中的Semiseparable Matrices——半可分矩陣,將揭示結構化矩陣與SSM之間的聯系
- 原論文Sec.4中的Structured Masked Attention(SMA),將揭示結構化矩陣與注意力之間的聯系
- 原論文Sec.5中的State SpaceDuality(SSD),將揭示SSM與注意力之間的聯系,如此,基于SSD,便發展出來了mamba2
更進一步,SSD的對偶形式是一種與注意力密切相關的平方計算,其定義為
其中是依賴于輸入的標量,范圍在 [0, 1]之間
SSD與標準的softmax注意力相比,有兩個主要區別
- 去掉了softmax
- 注意力矩陣按元素乘以一個額外的掩碼矩陣
這兩種變化都可以被視為解決了原始注意力中的問題。 例如,有研究發現softmax在注意力分數中會引起問題,如“注意力陷阱”現象(Darcet等,2024;Xiao等,2024)
更重要的是,掩碼矩陣可以被視為用不同的數據依賴位置掩碼替換Transformer的啟發式位置嵌入,從而控制跨時間傳遞的信息量(the mask matrix 𝐿 can be viewed as replacing the heuristic positional embeddings of Transformers with a different data-dependent positional mask that controls how much information is transfered across time)
更廣泛地說,這種形式是下文定義的線性注意力的SMA泛化的一個實例
- 總之,通過展示SSM具有矩陣變換形式
,對于一個依賴于
的矩陣
,各種形式的SSD可以通過統一的矩陣表示連接起來
- 特別地,SSD的對偶形式等價于通過矩陣 𝑀進行的樸素(平方時間)乘法,而遞歸形式是一種利用 𝑀結構的特定高效(線性時間)算法
以上之外,任何用于乘以的算法都可以應用,此次提出的硬件高效SSD算法是一種新的結構化矩陣乘法方法,一方面,其涉及 𝑀的塊分解,比純線性或二次形式獲得更好的效率權衡;二方面,與一般選擇性SSM——mamba1(Gu和Dao 2023,即Albert Gu and Tri Dao. “Mamba: Linear-Time Sequence Modeling with Selective State Spaces”)相比,它相對簡單且易于實現
第二部分 從SSM是Structured Matrices、使用結構化矩陣推廣線性注意力到SSD
2.1?SSM是結構化矩陣:State Space Models are Structured Matrices(含公式3 4 5 6 7 8)
2.1.1?SSM的矩陣變換形式:狀態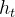 乘以矩陣
乘以矩陣 來生成
來生成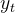 ,再用
,再用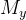 表示
表示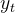 中的
中的 系數(公式3)
系數(公式3)
回顧一下,對選擇性SSM——即mamba1的定義是通過之前的公式2定義的參數化映射
SSM中,有
根據定義,,通過歸納法,可知時刻
?的狀態?
,可以表示為之前各個時刻的狀態
的加權和,即如下
上述公式中的
- 第一行的每一項表示的是之前某個時刻?
的狀態?經過一系列線性變換后的結果,最后這些結果加在一起得到了當前時刻的狀態
- 第二行中的
表示從
一直乘到
為方便大伙一目了然,加之十多年前,我就提醒自己,寫博客的目標之一是 如果某個算法看別的資料看不懂、看不動,那可以看懂、看動我的(堅持10多年來了,好處是博客影響力巨大,不好是累人),故還是要不厭其煩的解釋下
其實理解上面那個公式很簡單,直接一步一步推導一下即可,如下所示便可一目了然
- t = 0時
在這種情況下,是單位矩陣
,故有
- t = 1時
- t = 2時
- t = 3時
當然,這個過程可以借鑒下mamba1的這個圖,只是
、
還沒加上
這個參數而已,所以在不同的輸入x之下,便不會存在不同的
、
(下圖來自mamba1解讀一文的第2.1.2節SSM的循環結構表示:方便快速推理)
通過乘以矩陣來生成
并將方程在
上向量化,可推導出SSM的矩陣變換形式,如下(稱之為公式3)
對于上述公式3,我舉個例子,比如因為有
故可得
好比
2.1.2 半可分矩陣(定義3.1、定義3.2/公式4、定義3.3/公式5、定義3.4):順序半可分、1-半可分矩陣
首先,先來看下半可分矩陣(Semiseparable Matrices)的定義「稱之為定義3.1,在有的文獻中也被稱為?(N, 0)-半可分性)」
一個(下三角)矩陣 𝑀是 N-半可分的,如果包含在下三角部分(即對角線或以下)的每個子矩陣的秩——Rank最多為 N,則稱 N為半可分矩陣的階數或秩
Definition 3.1. A (lower triangular) matrix 𝑀 is N-semiseparable if every submatrix contained in the lower triangular portion
(i.e. on or below the diagonal) has rank at most N. We call N the order or rank of the semiseparable matrix
其和其他形式的相關“可分”結構(例如準可分矩陣和其他半可分矩陣的定義)有時被稱為結構化秩矩陣(或秩結構矩陣),因為它們的子矩陣由秩條件表征
半可分矩陣有許多結構化表示,包括分層半可分HSS、順序半可分SSS和Bruhat形式(Pernet和Storjohann 2018),此處將主要使用SSS形式
2.1.2.1?順序半可分SSS表示「The Sequentially Semiseparable (SSS) Representat」:每個 N-半可分矩陣都有一個 N-SSS 表示
先看順序半可分矩陣SSS表示的定義(稱其為定義3.2,公式4)
一個下三角矩陣 𝑀 ∈ R(T,T)如果它可以寫成以下形式,則具有 N-順序半可分(SSS)表示
對于向量
和矩陣
,定義算子 SSS使得
換言之,如果是且
(其實和上面的
但
一個意思),使得
則相當于
且和之前的公式3,一個意思
這個SSS表示帶來的好處是如定義3.3所示
一個 N-SSS 矩陣 𝑀具有上面公式(4)的表示,則便是 N-半可分的「Lemma 3.3?An N-SSS matrix 𝑀 with representation (4) is N-semiseparable」
證明如下(定義為公式5)
考慮任何非對角塊
,其中 𝑗 ′ > 𝑗 ≥ 𝑖 > 𝑖′「如原論文中所說,Consider any off-diagonal block 𝑀𝑗:𝑗 ′,𝑖′:𝑖 where 𝑗′ > 𝑗 ≥ 𝑖 > 𝑖′」,這具有顯式的秩-N分解為
為了避免正在閱讀此文的你頭疼,我還是用一個具體的示例來形象的說明下上述公式5
- 假設有以下矩陣
- 根據公式5的結構,選擇j' = 2、j = 1、i = 1、i’ = 0,然后有:
如此,上述的相當于有4個式子的結果需要逐一計算,具體計算過程如下步驟3 4 5 6所示
- 先算左上角那個式子
的結果,可得
先算前兩項
再算前兩項與第三項的結果- 再計算右上角那個式子
的結果
由于有
故而有- 接下來,計算左下角那個式子
的結果
假設與
相同,則
且假設與
相同,則
- 最后,計算右下角那個式子
的結果
由于有
且有
則可得- 最終,將上面這些結果全部合并起來,則可以得到矩陣
且有定義?3.4 即每個 N-半可分矩陣都有一個 N-SSS 表示
![]()
2.1.2.2?1-半可分矩陣(標量SSM遞歸):許多序列模型算法可以歸結為結構化矩陣乘法算法
首先,注意1-Semiseparable Matrices會簡稱1-SS矩陣
接下來,列出1-SS矩陣的特殊情況,此時和
是標量,可以從SSS的表示(如上面的公式4所示)或之前這個圖所示的
公式4當中出現的
即中提取出來
或
——去掉
和
原因在于對角矩陣易于處理(例如,對角矩陣的乘法與元素級標量乘法相同),故可以忽略這些項
因此,對1-SS矩陣的基本表示是「想曾經在上面的公式3或公式4中,還是
」,或如下(定義為公式6)
其等同于標量遞歸的最小形式——即狀態維度 且沒有
投影的退化SSM情況
值得注意的是,矩陣乘法可以通過如下的式子進行遞歸計算(定義為公式7)
即
對于上面的
相當于把之前公式3中
「其根據
計算而來」
中的
和
都去掉
因此,也將1-SS矩陣的矩陣乘法稱為標量SSM遞歸或累積乘積和(累積乘積和的廣義形式)作為遞歸的基本形式,同時也是本次mamba2主要算法的構建模塊
也從側面說明,許多序列模型的算法可以歸結為結構化矩陣乘法算法。1-SS矩陣體現了這一聯系:有許多快速算法可以計算原始標量遞歸或cumprod sum算子,所有這些算法實際上都等價于1-SS矩陣的不同結構分解
2.1.3?SSM是半可分矩陣:使得SSM問題轉化為結構化矩陣乘法
回顧一下,我們對SSM的定義是通過定義2.1定義的參數化映射

SSM與半可分矩陣之間的聯系僅僅是通過將這種變換寫成矩陣乘法,將向量
- 公式(3)
直接建立了SSM與順序半可分表示之間的聯系
而“順序半可分表示”又等價于一般的半可分矩陣(定義3.3和定義3.4)

- 定義 3.5 SSM變換
具有狀態大小 N,等同于按順序半可分表示的 N-SS 矩陣的矩陣乘法
換句話說,序列變換算子SSM(定義 2.2)
與矩陣構造算子 SSS(定義3.2) 一致
可以互換使用它們(有時也用SS作為簡寫)
此外,巧合的是 結構化SSM和順序半可分矩陣具有相同的縮寫,強調了它們的等價性
且可以使用這些縮寫 SSM(狀態空間模型或半可分矩陣)、SSS(結構化狀態空間或順序半可分) 或 SS(狀態空間或半可分)互換使用,以明確地指代任一概念
當然,最終的約定一般是:SSM指狀態空間模型,SS指半可分,SSS指順序半可分
如下圖所示,說明了將SSM視為「半可分矩陣——Semiseparable Matrix Transformations」的序列變換視角

- 作為序列變換,SSM可以表示為作用于序列維度T上的矩陣變換𝑀∈R(T,T),在一個頭的每個通道中共享相同的矩陣(如上圖左側所示)
- 這個矩陣是一個半可分矩陣(如上圖右側所示),它是一個秩結構矩陣,其中包含在對角線及其以下的每個子矩陣(藍色)的秩最多為N,等于SSM的狀態維度
這個意味著所有計算SSM的算法都可以看作是對半可分矩陣進行結構化矩陣乘法的算法,總之,上面的定義3.5 使得可以將高效計算SSM(及其他序列模型)的問題轉化為高效的結構化矩陣乘法算法
補充一句,上圖中的右側——半可分矩陣,其實就是類似之前公式4當中的圖
2.1.4(選讀) 通過結構化「矩陣乘法計算SSM(含公式8)」
既然上文已經證明了SSM的計算可以轉化為結構化矩陣乘法,那接下來,咱們便通過結構化矩陣算法計算SSM
如前所述,半可分矩陣(即秩結構矩陣)是一種經典的結構化矩陣類型:
- 它們具有壓縮表示形式,例如SSS形式只有
參數,而不是
參數
- 它們有直接在壓縮表示上操作的快速算法
此外,參數化和矩陣乘法成本在半可分階中可以非常緊湊
定義3.6 (Pernet, Signargout, 和 Villard (2023))表示:一個 N-SS 矩陣大小為 T可以用 𝑂 (NT)參數表示,并且矩陣-向量乘法在時間和空間上的復雜度為𝑂 (NT)
例如,1-SS 矩陣說明了這種連接的本質。 矩陣 𝑀 = 1SS(𝑎)由正好 T ? 1 個參數
回顧一下上面提到過的公式6
并且可以通過遵循上文提過的標量遞歸公式7在 𝑂 (T)時間內計算
公式7
根據上面的定義3.6可知,只需利用公式(2)
展開遞歸即可,具體過程如下公式8所示(三個公式分別被定義為8a、8b、8c)

這里, 𝐿 ∈ R(T,T)被定義為 1SS(𝐴),換句話說對于𝑖∈ [N]
該算法涉及三個步驟,對應于上文的公式2:
- 通過輸入矩陣 𝐵 (8a)擴展輸入 𝑋
- 展開獨立的標量SSM遞歸 (8b),且在步驟(8b)中使用了標量SSM和1-SS矩陣之間的等價關系
- 通過輸出矩陣 𝐶 (8c)收縮隱藏狀態 𝐻
其實,整個公式8算是mamba1(S6)模型的一個特例,其中擴展的張量Z和H的大小為
2.1.5(選讀) N-半可分矩陣的意義:通過低秩且分塊的方法加速注意力的計算過程
為方便大家更好的理解,我舉一個N-半可分矩陣來實現注意力計算的帶有token、序列的完整例子,以讓大家最大程度的一目了然,更堅定大家繼續讀下去的信心與決心(據我了解,這種完整示例,截止到24年9月9之前,還不曾出現過)
眾所周知,在標準的注意力機制中,計算 是一個重要的步驟,其中:
- Q是 Query 矩陣,維度為 n×d,其中 n 是序列長度(token數),d 是嵌入維度
- K?是 Key 矩陣,維度為 n×d
直接計算 的復雜度為
,因為每個token的Query需要與所有token的Key計算點積。對于長序列,這種計算開銷非常大,尤其在實際應用中,如語言模型處理大規模文本數據時
為了降低這種計算復雜度,可以引入一種 結構化的N-半可分矩陣,使得通過與這個結構化矩陣相乘的方式來 近似 或 替代 直接計算的操作
假設我們有一個結構化的N-半可分矩陣 SSS,可以用于加速或簡化的計算。這個矩陣 SSS 的作用有兩種可能:
- 方式1:低秩近似
在很多實際問題中,矩陣 Q 和 K 可能存在冗余信息,或者數據的某些維度比其他維度更重要。引入N-半可分矩陣可以將的高維度操作分解為多個低維度的操作
例如:如果 SSS 是一個低秩矩陣,它可以近似表示,然后我們計算?
代替
,從而降低計算復雜度——減少點積計算中的維度,進而加速計算
- 方式2:分塊計算
另一種方式是,N-半可分矩陣 SSS 可以將 Q 和 K 的計算過程分成多個獨立的小塊。換句話說,N-半可分矩陣將Q 和 K 分成若干個較小的子矩陣,通過分塊計算代替整體的矩陣乘法操作
例如,假設 SSS 將 K 分解為兩個較小的子矩陣和
?,那么我們可以分步計算
和
,再將結果組合起來,這種方式可以顯著減少計算的復雜度
舉個例子,假設我們有一個序列:"Who is the July Online founder",這將被模型轉化為一組token:[who, is , the, July, Online, founder],每個token會被嵌入到一個向量空間中,從而生成一個二維矩陣
- 我們將每個token的嵌入向量看作是矩陣的行(假設每個嵌入向量的維度是3),因此我們會得到一個形狀為 6×3 的矩陣,其中7是token的數量,3是嵌入維度
假設每個token的嵌入向量為Who is the July Online founder Q = [ [0.1, 0.2, 0.3], [0.5, 0.6, 0.7], [0.9, 1.0, 1.1], [1.3, 1.4, 1.5], [1.7, 1.8, 1.9], [2.1, 2.2, 2.3] ] - 在標準的點積注意力計算中,首先有三個矩陣:Query、Key和 Value——即輸入嵌入與「權重矩陣
/
/
」計算后的矩陣
假設近似 Query, Key, 和 Value 矩陣的三個半可分矩陣分別為:
Q (6x3):表示每個token的查詢向量
K (6x3):表示每個token的鍵向量
V (6x3):表示每個token的值向量
為何可以找到三個半可分矩陣來近似呢,原因在于在許多實際問題中,數據的特征矩陣(如Q, K, V)可能具有低秩性質,也就是矩陣中的信息主要集中在某些低維子空間中。換句話說,數據中許多特征可能存在一定的相關性,可以通過較少的特征來近似表示。因此,可以假設這些矩陣是N-半可分的,且還可以將其分解為若干子矩陣 - 既然這三個矩陣 Q, K, 和 V 可以N-半可分的,意思是它們可以被分解成若干個低維子矩陣
比如Q, K, 和 V 矩陣中的每個token的向量可以分解為兩個子向量
例如:對于每個token的嵌入向量,假設它們可以分解為兩個部分:前兩個維度是一個子向量,最后一個維度是另一個子向量
那么矩陣 Q 可以表示為:
Q1 = 第一列和第二列組成的子矩陣
Q2 = 第三列組成的子矩陣Q_1 = [ [0.1, 0.2], [0.5, 0.6], [0.9, 1.0], [1.3, 1.4], [1.7, 1.8], [2.1, 2.2] ]
類似地,K 和 V 也可以這樣分解:Q_2 = [ [0.3], [0.7], [1.1], [1.5], [1.9], [2.3] ]
K1? 和V1? 表示前兩個維度的子矩陣
K2? 和V2? 表示最后一個維度的子矩陣 - 接下來,直接計算對應的注意力
- 計算
和
?,得到兩個部分的注意力權重
- 對這兩個結果分別進行softmax,再將它們合并起來,得到最終的注意力權重
- 加權V矩陣: 最后,我們用分離出來的注意力權重對 V1和 V2? 分別進行加權和計算,最終將結果拼接起來,形成最終的輸出
- 計算
2.2?SMA(結構化掩碼注意力):使用結構化矩陣推廣線性注意力
2.2.1 從自注意力、核注意力到掩碼(核)注意力:含公式9-13
注意力的基本形式(單頭)是對三個向量序列的映射 (𝑄, 𝐾, 𝑉) ? →𝑌,如下所示(定義為公式9)
可以使用““shape annotation”來表示張量的維度,例如 𝑄 ∈ R(T,N),其中
- S和 T表示源和目標序列長度,分別意指:source、target之意
- N表示特征維度
- P表示頭維度
最常見的softmax注意力變體使用softmax激活 𝑓 = softmax來規范 𝐺矩陣的行
此外
- 雖然注意力通常被框定為對這三個對稱視圖輸入𝑄, 𝐾, 𝑉的操作,但公式9 中的輸入和輸出維度表明情況并非如此(特別是,輸出中不存在特征維度 N時)
- 因此在 S = T(例如自注意力)的情況下,將 𝑉視為主要輸入,因此公式9 定義了一個適當的序列變換 𝑉 → 𝑌
2.2.1.1 自注意力
對于自注意力,其中
- (i)? 源序列和目標序列相同(即 S = T)
- (ii) 通常特征維度和頭維度相同(即 N = P)
- (iii) 并且𝑄, 𝐾, 𝑉是通過對同一輸入向量的線性投影生成的,即
2.2.1.2 核注意力
// 待更
2.2.1.3 掩碼(核)注意力:對公式10 的分解
的分解
設 𝐿為形狀為 (T, S)的掩碼。 最常見的是,在自回歸自注意力情況下,當 S = T時, 𝐿可能是一個下三角矩陣,表示因果掩碼
除了強制因果關系外,還可以應用許多其他類型的掩碼——特別是各種稀疏模式,如帶狀、擴展
或塊對角線——這些都是為了減少密集注意力的復雜性
掩碼注意力通常用矩陣表示法表示為「定義為公式10,如果你讀的細致的話,你會發現這個公式10其實早在本文的《1.2 一系列定義:注意力機制、結構化矩陣、SSD》,便已出現過」
更準確地說,帶有shape annotation并將其分解為精確的計算序列(定義為公式11):

在本節中改進的注意力變體推導從注意到這個公式可以寫成一個單一收縮開始(定義為公式12):
而算法11可以通過特定的成對收縮順序重新表述為算法12的形式,如下公式13所示

2.2.2?線性注意力:含公式14、公式15(SMA的線性對偶形式)
如下公式14所示的線性注意力
等價于10:
接下來,以另一種順序執行上面的公式12,從而得到下面的公式15——算是SMA的線性對偶形式

其中
- 第一步(15a)通過特征維度 N的因子執行“擴展”到更多特征
- 第二步(15b)是最關鍵的,并解釋了線性注意力的線性部分
首先,注意到(15b)只是通過 𝐿進行直接矩陣乘法「因為 (P, N)軸可以被展平」
且還要注意,這是唯一涉及 T和 S軸的項,因此應該具有 Ω(TS)復雜度(即序列長度的二次方)
然而,當掩碼 𝐿是標準的因果注意力掩碼(下三角全為1)時,通過 𝐿進行矩陣-向量乘法與特征逐項累積和相同
為方便理解,可再回顧下公式7
而怎么來呢,根據
而來呀,而
不就是公式6么
- 第三步(15c)收縮擴展的特征維度。 如果將 𝐾視為輸入(如上文2.2.1節開頭所述),那么 𝑉和 𝑄分別執行擴展和收縮
2.2.3?SMA(結構化掩碼注意力):可實例化為任何給定的矩陣結構類別
通過掩碼注意力的張量收縮視角(如公式15所示),得知原始線性注意力的關鍵在于帶有因果掩碼的矩陣-向量乘法等同于累加求和運算(we can immediately see that the crux of the original linear attention is the fact that matrix-vector multiplication by the causal mask is equivalent to the cumulative sum operator)
- 然而,觀察到沒有理由注意力掩碼必須全是1。 線性注意力快速的必要條件是 𝐿是一個結構化矩陣,根據定義,這些矩陣具有快速矩陣乘法(根據上文1.2.2節所述的結構化矩陣 所述)
- 特別是,我們可以使用任何矩陣-向量乘法復雜度低于二次方(理想情況下是線性)的掩碼矩陣
「we can use any mask matrix 𝐿 that has sub-quadratic (ideally linear) matrix-vector multiplicat」,這將通過加速瓶頸公式(15b)使其具有與標準線性注意力相同的復雜度
定義 4.2?結構化掩碼注意力SMA(或簡稱結構化注意力)被定義為一個函數作用于查詢/鍵/值𝑄, 𝐾, 𝑉以及任何結構化矩陣 𝐿 (即具有低于二次復雜度的矩陣乘法——?sub-quadratic matrix multiplication),通過四維張量收縮
- SMA二次模式算法是通過(公式13)定義的成對收縮序列,對應于標準的(掩碼)注意力計算

- SMA線性模式算法是通過(公式15)定義的成對收縮序列,其中步驟(15b)通過二次結構矩陣乘法進行優化

總之,可以將SMA實例化為任何給定的矩陣結構類別,比如如下圖所示的一些實例「SMA constructs a masked attention matrix(掩碼注意力矩陣) ?for any structured matrix 𝐿, which defines a matrix sequence transformation 𝑌 = 𝑀𝑉」

- 線性注意力使用因果掩碼
- RetNet使用衰減掩碼
,其中,對于某些衰減因子
RetNet (Y. Sun et al. 2023) uses a decay mask 𝐿𝑖 𝑗 = 𝛾𝑖 ? 𝑗 · I[ 𝑗 ≥ 𝑖] for some decay factor 𝛾 ∈ [0, 1] - SSD使用1-半可分(1-semiseparable)
- 衰減掩碼可以推廣到Toeplitz矩陣
對于某些可學習的(或依賴于輸入的)參數集
這可以解釋為一種相對位置編碼形式,類似于其他方法如AliBi,但乘法而不是加法 - 另一種變體可以使用傅里葉矩陣(Fourier matrix)
以不同的方式編碼位置結構
2.3 總結:再談SSD(狀態空間對偶性):含公式16之SSM的二次對偶形式
2.3.1?標量-恒等的結構化狀態空間模型及其示例
回想一下,SSM由定義,SSM的矩陣形式使用SSS(順序半可分)表示
,其中公式3
現在讓我們考慮只是一個標量的情況;換句話說,這是一種結構化 SSM 的實例,其中
矩陣具有極其特殊的結構:
,其中
?是一個標量,
?是單位矩陣
然后可以重新排列
這可以向量化為
其中,?A 的特性(這里是標量?a)被用來構建?L,L 是一個由?a?定義的序列,用于表示狀態轉移, 而𝐵, 𝐶 ∈ R(T,N)
使用這種公式,完整的輸出 𝑌 = 𝑀X精確計算為公式16——算是SSM的二次對偶形式(也可以認為是SMA的二次對偶形式)

其中 S = T,從而可以看到這與掩碼核注意力公式13的原始定義完全相同
因此,如「第2.1.4 通過結構化矩陣算法計算SSM」所述,計算標量結構化SSM——通過實現半可分矩陣𝑀并執行二次矩陣-向量乘法——與二次掩碼核注意力完全相同
2.3.2 1-半可分結構化掩碼注意力
SMA允許使用任何結構化掩碼
當是因果掩碼時,它是標準的線性注意力。 注意,因果掩碼是
,即1-SS掩碼由公式6中的
生成
進一步,對于,
而言,其非常類似于注意力計算
- 事實上,如果所有的
- 那么
只是下三角因果掩碼且等同于因果線性注意力(then is simply the lower-triangular causal mask and is equivalent to causal linear attention)
- 而其中的
這不就相當于
相當于C B X類比于Q K V
畢竟,可曾還記得上面的公式3
這激發了將推廣到1-半可分掩碼類,或1-半可分結構化
掩碼注意力(1-SS SMA),其中線性注意力遞歸中的cumsum被更一般的遞歸——標量SSM掃描,即1-半可分矩陣乘法所取代
最后,我們考慮1-半可分SMA的最重要原因是計算它的線性形式是對角SSM的一個特例。SMA的線性形式是算法(15),其中瓶頸步驟(15b)可以看作是通過1-SS掩碼進行矩陣乘法
第三部分 從硬件高效的SSD算法、到Mamba-2 架構
3.1 硬件高效的SSD算法:塊分解、對角塊、低秩塊
定義6.1 考慮一個具有狀態擴展因子 N和頭部維度 P = N的SSD模型,存在一種算法可以在任何輸入上計算模型,該算法只需要
訓練FLOPs,
推理FLOPs,
推理內存,其工作主要由矩陣乘法主導
注意,所有這些界限都是緊的,因為具有狀態擴展 N的SSM在頭部大小為時,總狀態大小為
「分別得出訓練和推理 FLOPs 的下界為
和
」。此外,輸入
本身有
個元素,從而產生了內存下限
如下圖所示,狀態空間對偶描述了SSM和掩碼注意力之間的密切關系

- 上圖左側:一般的 SSM和 SMA 都具有線性和二次形式,在符號上有直接的類比
比如,SSM的線性形式為公式8b,SSM的二次對偶形式為公式16
對于上面的公式16
如果是作為SSM的二次對偶形式:在SSM的框架下,公式16描述了如何通過狀態轉移矩陣?A、輸入到狀態的映射矩陣 B和狀態到輸出的映射矩陣?C?來計算序列的輸出
如果是作為SMA的二次對偶形式:在SMA的框架下,公式16展示了如何通過引入結構化矩陣(例如,通過SSM定義的矩陣)來優化傳統的注意力計算。這種方法允許使用掩碼矩陣?L?來控制信息流,并通過結構化矩陣與查詢?Q、鍵?K?和值?V?矩陣的結合來加速計算 (注意,標紅這句話值得反復體會三遍)
再比如,SMA的線性形式為公式15、SMA的二次形式為公式13a(當然,這個13a由公式10衍變而來)


- 上圖右側:SSM 和 SMA 在一大類狀態空間對偶模型(SSD) 上相交,這些模型捕捉了許多序列模型作為特例
定義6.1背后的主要思想是再次將計算SSM的問題視為半可分矩陣乘法,但以一種新的方式利用其結構,即不是在遞歸或注意模式下計算整個矩陣,而是對矩陣進行塊分解
- 對角塊可以使用對偶注意模式計算,這可以通過矩陣乘法高效完成
- 而非對角塊可以通過半可分矩陣的秩結構進行分解并簡化為較小的遞歸
背景鋪墊:塊分解
首先,將矩陣 𝑀劃分為一個的子矩陣網格,每個子矩陣的大小為 Q × Q,對于某個塊大小 Q。 注意,根據半可分矩陣的定義性質(定義3.1),非對角塊是低秩的
如下圖所示,分別體現的是塊分解、對角塊、低秩塊

舉個例子,例如對于 T = 9 并分解成長度為 Q = 3 的塊

上圖中的陰影部分是半可分矩陣的非對角塊的低秩分
從這里我們可以將問題簡化為這兩個部分。 這些也可以解釋為將“塊” 的輸出分為兩個部分:
- 塊內輸入的影響
- 以及塊之前輸入的影響
然后,如果要完成狀態空間對偶(SSD)模型的完整 PyTorch代碼,則可以先定義符號來定義批量矩陣乘法
與批次維度 B
從而可以推斷出效率的三個方面:
- 計算成本:總共
FLOPs
- 內存成本:總共
空間
- 并行化:更大的 M, N, K項可以利用現代加速器上的專用矩陣乘法單元
def segsum(x):
"""樸素的段和計算。exp(segsum(A)) 生成一個 1-SS 矩陣,等價于一個標量 SSM """
T = x.size(-1)
x_cumsum = torch.cumsum(x, dim=-1)
x_segsum = x_cumsum[..., :, None] - x_cumsum[..., None, :]
mask = torch.tril(torch.ones(T, T, device=x.device, dtype=bool), diagonal=0)
x_segsum = x_segsum.masked_fill(~mask, -torch.inf)
return x_segsumdef ssd(X, A, B, C, block_len=64, initial_states=None):
"""
Arguments:
X: (batch, length, n_heads, d_head)
A: (batch, length, n_heads)
B: (batch, length, n_heads, d_state)
C: (batch, length, n_heads, d_state)
Return:
Y: (batch, length, n_heads, d_head)
"""
assert X.dtype == A.dtype == B.dtype == C.dtype
assert X.shape[1] % block_len == 0# 重新排列成塊/段
X, A, B, C = [rearrange(x, "b (c l) ... -> b c l ...", l=block_len) for x in (X, A, B, C)]
A = rearrange(A, "b c l h -> b h c l")
A_cumsum = torch.cumsum(A, dim=-1為方便形象理解,再貼個圖,如下(來源于此文中的3.1.1.3節“mamba:從S4到S6的算法變化流程”)
3.1.1?對角塊
對角塊很容易處理,因為它們只是較小規模的自相似問題。 𝑗-th 塊表示計算范圍內的答案
- 特別地,對于小塊長度 Q,這個問題可以通過對偶二次SMA形式更有效地計算
其中,二次SMA計算的成本包括三個步驟「Center Blocks. The cost of the quadratic SMA computation consists of three steps (equation (16)),至于為何是公式16,上文早已著重解釋過了,在于公式16可以認為是SSM的二次對偶形式,也可以理解為SMA的二次對偶形式」:
i)? ?計算核矩陣
,其成本為 BMM( T/Q, Q, Q, N)
ii)? 乘以掩碼矩陣,這是對形狀為 ( T/Q, Q, Q)的張量進行的逐元素操作
iii)?乘以 𝑋值,其成本為 BMM( T/Q, Q, P, N)
此外,這些塊可以并行計算 - 這些子問題可以解釋為:假設初始狀態(到塊)為 0,每塊的輸出是什么。換句話說,對于塊 𝑗,這將計算正確的輸出,僅考慮塊輸入
對應的代碼為
# 1. 計算每個塊內(對角塊)的輸出
L = torch.exp(segsum(A))
Y_diag = torch.einsum("bclhn,bcshn,bhcls,bcshp->bclhp", C, B, L, X)3.1.2?低秩塊:右B-塊因子、中心A-塊因子、左C-塊因子三個部分的結算
低秩分解由3個項組成,相應地有三部分計算

- 像下面這樣的項被稱為右因子或 𝐵-塊因子
此步驟計算低秩分解的右 𝐵-塊因子的乘法。 注意,對于每個塊,這是一個(N, Q)乘(Q, P)的矩陣乘法,
其中 N是狀態維度, 𝑃是頭維度。 每個塊的結果是一個(N, P)張量,其維度與擴展的隱藏狀態?相同
這可以解釋為:假設初始狀態(到塊)為 0,每個塊的最終狀態是什么。 換句話說,這計算了,其中
對應的代碼為
這一步是一個單一的矩陣乘法,成本為 BMM( T/Q, N, P, Q)# 2. 計算每個塊內的狀態 # (低秩分解的非對角塊的右項;B項) decay_states = torch.exp((A_cumsum[:, :, :, -1:] - A_cumsum)) states = torch.einsum("bclhn,bhcl,bclhp->bchpn", B, decay_states, X) - 像
這樣的項被稱為中心因子或 𝐴-塊因子
這一步計算了低秩分解中中心 𝐴-塊因子項的影響。 在前一步中,每個塊的最終狀態的總形狀為
現在通過一個由這現生成的1-SS矩陣相乘:
這一步可以通過任何用于計算1-SS乘法的算法來計算(也稱為標量SSM掃描或累積乘積和操作符)
這可以解釋為:每個塊的實際最終狀態是什么考慮到所有先前的輸入; 換句話說,這計算了真實的隱藏狀態(考慮到所有的
)
對應的代碼為
這一步是長度為 T/Q的標量SSM掃描(或1-SS乘法),在 (N, P)獨立通道上進行。 這次掃描的工作是 TNP/Q,這是相對于其他因素可以忽略不計的# 3. 計算塊間SSM遞歸;在塊邊界生成正確的SSM狀態 # (非對角塊分解的中間項;A項) if initial_states is None : initial_states = torch.zeros_like(states[:, :1]) states = torch.cat([initial_states, states], dim=1) decay_chunk = torch.exp(segsum(F.pad(A_cumsum[:, :, :, -1], (1, 0)))) new_states = torch.einsum("bhzc,bchpn->bzhpn", decay_chunk, states) states, final_state = new_states[:, :-1], new_states[:, -1]
請注意,由于阻塞將序列長度從 T減少到 T/Q,這次掃描的成本比純SSM掃描(例如Mamba的選擇性掃描)小 Q倍
因此,我們觀察到在大多數問題長度上,其他算法(附錄B)可能更有效或更容易實現,而不會顯著減慢速度
例如,通過1-SS矩陣乘法的簡單實現成本為 BMM(1, T/Q, NP, T/Q),這比簡單的遞歸/掃描實現更容易實現且可能更有效 - 像下面這樣的項被稱為左因子或 𝐶-塊因子
這一步計算了左 𝐶-塊因子的低秩分解的乘法。 對于每個塊,這可以通過矩陣乘法來表示
這可以解釋為:每個塊的輸出是什么考慮到正確的初始狀態,并假設輸入
為 0
換句話說,對于塊 𝑗,這計算了僅考慮先前輸入的正確輸出
對應的代碼為
這一步是一個單一的矩陣乘法,成本為 BMM(T/Q, Q, P, N)# 4. 計算每個塊的狀態到輸出的轉換 # 低秩分解的非對角塊的左項;C項 state_decay_out = torch.exp(A_cumsum) Y_off = torch.einsum( 'bclhn,bchpn,bhcl->bclhp', C, states, state_decay_out
最后,如下# 添加塊內和塊間項的輸出(對角塊和非對角塊) Y = rearrange(Y_diag+Y_off, "b c l h p -> b (c l) h p") return Y, final_state
整個的過程,可以用下圖表示
其中
- 橙色的diagonal block代表input到output,涉及到上面所說的對角塊——對角塊表示塊內計算
而下面的非對角塊表示則通過SSM的隱藏狀態進行的塊間計算
- 綠色的low-rank block代表input到state,類似
中的
相當于上面介紹過的右因子或 𝐵-塊因子 - 黃色的low-rank block代表state到state,類似
中的
相當于上面介紹過的中心因子或 𝐴-塊因子 - 藍色的low-rank block代表state到output,類似
相當于上面介紹過的左因子或 𝐶-塊因子
總之,通過使用SSM的矩陣變換視角將其寫成半可分矩陣,通過塊分解矩陣乘法算法開發了更硬件高效的SSD模型計算,矩陣乘法也可以解釋為SSM,其中塊表示輸入和輸出序列的分塊
注意,上圖可以配合下圖一塊看(來源于此文中2.1.1節的“離散數據的連續化:基于零階保持技術做連續化并采樣”的最后)
// 待更
3.2?Mamba-2 架構
如下圖所示,Mamba-2模塊通過去除序列線性投影簡化了Mamba模塊(The Mamba-2 block simplifies the Mamba block by removing sequential linear projections)

- SSM參數𝐴, 𝐵, 𝐶在模塊開始時生成,而不是作為SSM輸入𝑋 的函數
the SSM parameters 𝐴, 𝐵, 𝐶 are produced at the beginning of the block instead of as a function of the SSM input 𝑋 . - 添加了一個額外的歸一化層,如NormFormer,提高了穩定性
An additional normalization layer is added as in NormFormer (Shleifer, Weston, and Ott 2021), improving stability. - 𝐵和𝐶投影只有一個頭部,在𝑋頭部之間共享,類似于多值注意力(MVA)
The 𝐵 and 𝐶 projections only have a single head shared across the 𝑋 heads, analogous to multi-value attention (MVA)
3.2.1?模塊設計:并行參數投影、額外的歸一化
我們首先討論對神經網絡模塊的修改,這些修改獨立于內部序列混合層(即核心SSD層之外)
3.2.1.1 并行參數投影
對比mamba1和mamba2可知
- Mamba-1的動機是基于SSM中心的觀點,其中選擇性SSM層被視為從 𝑋 → 𝑌的映射(Mamba-1 was motivated by an SSM-centric point of view where the selective SSM layer is viewed as a map from 𝑋 → 𝑌 )
SSM參數, 𝐵, 𝐶被視為輔助參數,是SSM輸入 𝑋的函數。 因此,定義(𝐴, 𝐵, 𝐶)的線性投影——在初始線性投影創建𝑋之后進行(The SSM parameters 𝐴, 𝐵, 𝐶 are viewed as subsidiary and are functions of the SSM input 𝑋 . Thus the linear projections defining (𝐴, 𝐵, 𝐶) occur after the initial linear projection to create 𝑋)
- 在Mamba-2中,SSD層被視為從𝐴, 𝑋, 𝐵, 𝐶 → 𝑌的映射。 因此,有必要在塊的開頭通過單個投影并行生成𝐴, 𝑋,𝐵, 𝐶(In Mamba-2, the SSD layer is viewed as a map from 𝐴, 𝑋, 𝐵, 𝐶 ? → 𝑌 . It therefore makes sense to produce 𝐴, 𝑋, 𝐵, 𝐶 in parallel with a single projection at the beginning of the block)
值得注意的是
? 這與標準注意力架構類比,其中𝑋, 𝐵, 𝐶對應于并行創建的𝑄, 𝐾, 𝑉投影(Note the analogy to standard attention architectures, where 𝑋, 𝐵, 𝐶 correspond to the 𝑄, 𝐾, 𝑉 projections that are created in parallel.)
? 為SSM的𝐴, 𝐵, 𝐶, 𝑋輸入采用并行投影略微減少了參數,更重要的是,通過使用標準的Megatron分片模式,更適合于較大模型的張量并行(Note that adopting parallel projections for the 𝐴, 𝐵, 𝐶, 𝑋 inputs to the SSM slightly reduces parameters and more importantly is more amenable to tensor parallelism for larger models, by using standard Megatron sharding patterns)
3.2.1.2 額外的歸一化
在初步實驗中,發現較大模型中容易出現不穩定性
通過在最終輸出投影之前的塊中添加一個額外的歸一化層(例如LayerNorm、GroupNorm或RMSNorm)來緩解這一問題。 這種歸一化的使用與NormFormer架構最直接相關,該架構也在MLP和MHA塊的末端添加了歸一化層
且mamba2的作者還注意到,這一變化類似于其他最近與Mamba-2相關的模型,這些模型是從線性注意力視角推導出來的
- 原始的線性注意力公式通過一個分母項進行歸一化,該分母項模擬了標準注意力中softmax函數的歸一化
而TransNormerLLM和RetNet發現這種歸一化是不穩定的,并在線性注意力層之后添加了額外的LayerNorm或GroupNorm - mamba2的額外歸一化層與這些略有不同,發生在乘法門(multiplicative gate)分支之后而不是之前
Our extra normalization layer differs slightly from these, occuring after the multiplicative gate branch instead of before
3.2.2?序列變換的多頭模式:多查詢、多鍵、多值
回想一下,SSM被定義為一個序列變換

其中:
- 𝐴, 𝐵, 𝐶 參數具有狀態維度 N
- 它們定義了一個序列變換
,例如可以表示為矩陣
- 該變換作用于輸入序列
,獨立于 P軸
可以將其視為定義了序列變換的一個 head
定義 7.1(多頭模式)? 多頭序列變換由 H個獨立的頭組成,總模型維度為 D = d_model。參數可以在各頭之間共享,形成一個head模式
- 狀態大小 N和頭維度 P類似于注意力機制中的
頭維度和
頭維度(The state size N and head dimension P are analogous to the 𝑄𝐾 head dimension and 𝑉 head dimension of attention, respectively)
- 正如在現代Transformer架構中(比如Google的PaLM、Meta的Llama),在Mamba-2中我們通常選擇這些常數為64或128;當模型維度 D增加時,我們增加頭的數量,同時保持頭維度 N和 P不變(when the model dimension D increases, we increase the number of heads while keeping the head dimensions N and P fixed)
為了描述如何做到這一點,我們可以從多頭注意力中轉移和推廣想法,以定義SSM或任何一般序列變換的類似模式(in order to describe how to do this, we can transfer and generalize ideas from multihead attention to define similar patterns for SSMs, or any general sequence transformation)

- 多頭狀態空間模型 (MHS) / 多頭注意力機制 (MHA) 模式
Multihead SSM (MHS) / Multihead Attention (MHA) Pattern
經典的 MHA 模式假設頭維度 P可以整除模型維度 D
頭的數量定義為 H = D/P(比如transformer論文中,模型維度512,8個頭,每個頭的維度為512/8 = 64),然后,通過創建 H個核心序列變換的副本,通過創建每個參數的 H個獨立副本來實現
請注意,雖然MHA模式最初是為注意力序列變換描述的,但它可以應用于與定義2.1兼容的任何事物。例如,多頭SSD層將接受形狀符合方程(17)的輸入,其中SSD算法在 H = n_heads維度上廣播 - Multi-contract SSM (MCS)/多查詢注意力(MQA)模式
Multi-contract SSM (MCS) / Multi-query Attention (MQA) Pattern
多查詢注意力(詳見此文:一文通透各種注意力:從多頭注意力MHA到分組查詢注意力GQA、多查詢注意力MQA),顧名思義,即多個query 單個key value,如下圖最右側所示:Multi-query
可以顯著提高自回歸推理的速度,這依賴于緩存𝐾和𝑉張量。 這種技術只是避免給𝐾和𝑉額外的頭維度,換句話說,就是將(𝐾, 𝑉)的單個頭廣播到𝑄的所有頭上
利用狀態空間對偶性,我們可以將MQA的等效SSM版本定義為方程(18)
其中, 𝑋 和 𝐵(注意力的 𝑉 和 𝐾?的SSM類比)在 H個頭之間共享,也稱之為多收縮SSM (MCS)頭模式,因為控制SSM狀態收縮的 𝐶 參數在每個頭中都有獨立的副本
相當于X B C類比于V K Q
此外,多查詢注意力的思想可以擴展到分組查詢注意力(分組頭模式Grouped Head Patterns):而不是1個K和V頭,可以創建 G個獨立的K和V頭,其中1 < G且 G整除 H(如上圖中部所示)
這既是為了彌合多查詢和多頭注意力之間的性能差異,也是為了通過將 G設置為分片數量的倍數來實現更高效的張量并行 - 多鍵注意力 (MKA) 或多擴展SSM (MES)頭模式
其中控制SSM擴展的 𝐵在每個頭中是獨立的,而 𝐶和 𝑋在頭之間共享
- 多輸入SSM (MIS) / 多值注意力(MVA) 模式
Multi-input SSM (MIS) / Multi-value Attention (MVA) Pattern
雖然MQA對于注意力來說是有意義的,因為它有KV緩存,但它不是SSM的自然選擇
在Mamba中, 𝑋被視為SSM的主要輸入,因此 𝐵和 𝐶是跨輸入通道共享的參數,而在公式(20)中定義了一種新的多值注意力 (MVA) 的多輸入 SSM (MIS) 模式,這同樣可以應用于任何序列變換,例如 SSD
上面的描述可能比較繞,我給大家畫個圖,便一目了然了
首先,對于下圖三種模式中的C B X都是可以逐一和注意力中的Q K V對應的,且當某個模式中的或C、或B、或X被圈起來時,則代表它的數量是更多的 屬于多個,而沒被圈起來的則可能是單個
具體而言,可以簡單粗暴的理解為:
- 多查詢便是多個Query?單個Key?單個Value
相當于對應:多個C 單個B 單個X- 多鍵便是多個Key 單個Query 單個Value
相當于對應:多個B 單個C 單個X- 多值便是多個Value 單個Query 單個Key
相當于對應:多個X 單個C 單個B
定義7.2 mamba1的重新定義
Mamba 架構的選擇性SSM(S6)層可以被視為具有
- 頭維度 𝑃 = 1: 每個通道都有獨立的 SSM 動態 𝐴
- 多輸入SSM(MIS) 或多值注意力(MVA)頭結構(如上圖最右側所示):輸入𝑋的所有通道共享𝐵、𝐶矩陣(對應于注意力對偶中的𝐾、Q)
因為通過實驗證明,Mamba中最初使用的MVA模式表現最佳
此外,值得一提的是,Mamba-2中使用的多輸入SSM頭模式(multi-input SSM head pattern,比如8個X 1個C 一個B),可以輕松擴展到分組輸入SSM(grouped-input SSM,GIS,比如8個X 4個C 4個B),或同義的分組值注意力(grouped-value attention,GVA,還是value對應的X最多,然后 C B相對少)
3.2.3 線性注意力的其他SSD擴展
// 待更
3.3 SSM的系統優化:張量并行、序列并行、可變長度
3.3.1 張量并行Tensor Parallel
張量并行「Tensor parallelism,簡稱TP,詳見此文《大模型并行訓練指南:通俗理解Megatron-DeepSpeed之模型并行與數據并行》的第二部分 張量并行(Tensor Parallelism,算模型并行的一種)」是一種模型并行技術,它將每一層(例如,注意力機制,MLP)拆分在多個加速器(如 GPU)上運行
- 這種技術被廣泛用于在 GPU 集群上訓練大多數大型模型(Brown 等,2020;Chow dhery 等,2023;Touvron, Lavril 等,2023;Touvron, L. Martin 等,2023)
其中每個節點通常有 4-8 個 GPU,并具有快速網絡連接,如 NVLink - TP 最初是為 Transformer 架構開發的,沒法直接適應其他架構,故在Mamba 架構中使用 TP 有一定的挑戰,進一步,Mamba-2 架構用起來TP之后,還得考慮如何設計以使 TP 高效
回顧 Mamba 架構,單個輸入(為簡單起見,不進行批處理),輸入投影矩陣
,其中
是擴展因子(通常為2),輸出投影矩陣
使用 TP,假設想將計算分配到 2 個 GPU 上
- 很容易將輸入投影矩陣
和
分成兩個大小為
的分區
It is easy to split the input projection matrices 𝑊 (𝑥 ) and 𝑊 (𝑧 ) into two partitions each of size 𝑑 × 𝑒𝑑/2 - 然后每個 GPU 將持有大小為
的一半
Then each GPU would hold half of 𝑥𝑐 of size 𝐿 × 𝑒𝑑/2 - 然而,由于 Δ, 𝐵, 𝐶是
的函數,所以需要在 GPU 之間進行額外的全歸約,以在計算Δ, 𝐵, 𝐶之前獲得整個
However,we see that since Δ, 𝐵, 𝐶 are functions are 𝑥𝑐 , so we would need an extra all-reduce between the GPUs to get the whole of 𝑥𝑐 before computing Δ, 𝐵, 𝐶 - 之后,由于它們在𝑑上是獨立的,因此兩個 GPU 可以并行計算 SSM
After that the two GPUs can compute the SSM in parallel since they are independent
along 𝑑 - 最后,我們可以將輸出投影矩陣
分成兩個大小為
的分區,并在最后進行一次全規約
At the end, we can split the output projection matrices 𝑊 (𝑜 ) into two partitions each of size 𝑒𝑑/2 × 𝑑, and do an all-reduce at the end
上述整個過程,與Transformer相比,將進行兩次全規約,而不是一次,從而使通信時間加倍(Compared to Transformers, we would incur two all-reduces instead of one, doubling the time spent in communication)
對于大規模Transformer訓練,通信可能已經占用了相當大的一部分時間(例如10-20%),加倍通信將使Mamba在大規模訓練中效率不高「For large-scale Transformers training, communication might already take a significant fraction of time(e.g. 10-20%), and doubling communication would make Mamba not as efficient for large-scale training」
使用Mamba-2的目標是每個塊只有一次全規約,類似于Transformer中的注意力或MLP塊。因此,通過投影直接從𝑢得到Δ, 𝐵, 𝐶,而不是從得到,從而允許拆分這些投影矩陣
這意味著我們在不同的GPU上有不同的 Δ, 𝐵, 𝐶集合,這相當于在一個更大的“邏輯GPU”上有幾個“組”的 Δ, 𝐵, 𝐶。此外,在每個塊內使用GroupNorm,組的數量可被TP度整除,這樣TP組中的GPU在塊內無需通信:
可以看到,只需要拆分輸入投影矩陣和輸出投影矩陣,并且只需要在塊的末尾進行全歸約。 這類似于注意力和MLP層的TP設計
特別地,如果有TP度為2,則會拆分
,其中
,其中
,其中
對于 𝑖 = 1, 2,TP Mamba- 2層可以寫成

總之,如下圖所示

- 左側是張量并行,分割輸入投影矩陣
、
和輸出投影矩陣
每個SSM頭 (𝐴, 𝐵, 𝐶, 𝑋) →𝑌存在于單個設備上,選擇GroupNorm作為最終歸一化層可以避免額外的通信。每層需要一次全歸約,就像Transformer中的MLP或注意力塊一樣 - 右側是序列/上下文并行,類似于SSD算法,使用多個設備,可以沿序列維度進行分割,每個設備計算其序列的狀態,然后將該狀態傳遞給下一個GPU
3.3.2?序列并行
對于非常長的序列,可能需要沿序列長度維度將輸入和激活拆分到不同的GPU上。 有兩種主要技術:
- 用于殘差和歸一化操作的序列并行(SP):由Korthikanti等人首次提出,這種技術將TP中的all-reduce分解為reduce-scatter和all-gather
注意到在同一TP組中的所有GPU上,殘差和歸一化操作在相同輸入上重復進行,SP通過執行:reduce-scatter、殘差和歸一化,然后all-gather,沿序列長度維度拆分激活
由于Mamba-2架構使用相同的殘差和歸一化結構,SP無需修改即可應用 - 序列并行用于token混合操作(注意力或SSM),也稱為“上下文并行”(context parallelism,簡稱CP)。已經為注意力層開發了幾種技術「例如,環形注意力(Liu, Yan, et al. 2024; Liu, Zaharia和 Abbeel 2023),使用復雜的負載均衡技術(Brandon 等人,2023)
注意力機制中的序列并行問題在于可以將查詢和鍵分成塊,但每個查詢塊需要與鍵塊交互,導致通信帶寬與工作者數量呈二次方關系
使用 SSMs,可以簡單地分割序列:每個工作者獲取一個初始狀態,計算其輸入的 SSM,返回最終狀態,并將最終狀態傳遞給下一個工作者。 通信帶寬與工作者數量呈線性關系。 這種分解與 SSD 算法中的塊分解完全相同,可以分成塊/塊
且在上圖 中說明了這種上下文并行性
3.3.3 可變長度
雖然預訓練通常對批次使用相同的序列長度,但在微調或推理過程中,模型可能需要處理不同長度的輸入序列。
一種處理這種情況的簡單方法是將批處理中所有序列右填充到最大長度,但如果序列長度差異很大,這可能效率低下。 對于Transformer,已經開發了復雜的技術來避免填充,并在GPU之間進行負載平衡(Zeng等,2022;Y.Zhai等,2023),或者在同一批次中打包多個序列并調整注意力掩碼(Ding等,2024;Pouransari等,2024)
對于SSM,特別是Mamba,可以通過簡單地將整個批次視為一個長序列來處理可變序列長度,并避免在單個序列之間傳遞狀態。 這相當于簡單地設置,對于一個序列末尾的token 𝑡,以防止它將信息傳遞給屬于不同序列的token 𝑡 + 1
// 待更














)


實現如旋風、吸引力、風吹效果等)
)

安裝)


環境安裝)
疊加車牌識別的信息)

)

)