《R for Data Science (2e)》免費中文翻譯 (第1章) --- Data visualization（2）

寫在前面

本系列推文為《R for Data Science (2)》的中文翻譯版本。所有內容都通過開源免費的方式上傳至Github，歡迎大家參與貢獻，詳細信息見：
Books-zh-cn 項目介紹：
Books-zh-cn：開源免費的中文書籍社區
r4ds-zh-cn Github 地址：
https://github.com/Books-zh-cn/r4ds-zh-cn
r4ds-zh-cn 網站地址：
https://books-zh-cn.github.io/r4ds-zh-cn/

1.4 可視化分布圖

可視化變量的分布方式取決于變量的類型：分類變量或數值變量。

1.4.1 一個分類變量

如果一個變量只能取一小組值中的一個，則該變量是分類變量（categorical）。要檢查分類變量的分布情況，可以使用條形圖。條形圖的高度顯示了每個 x 值出現的觀測次數。

ggplot(penguins,?aes(x?=?species))?+geom_bar()

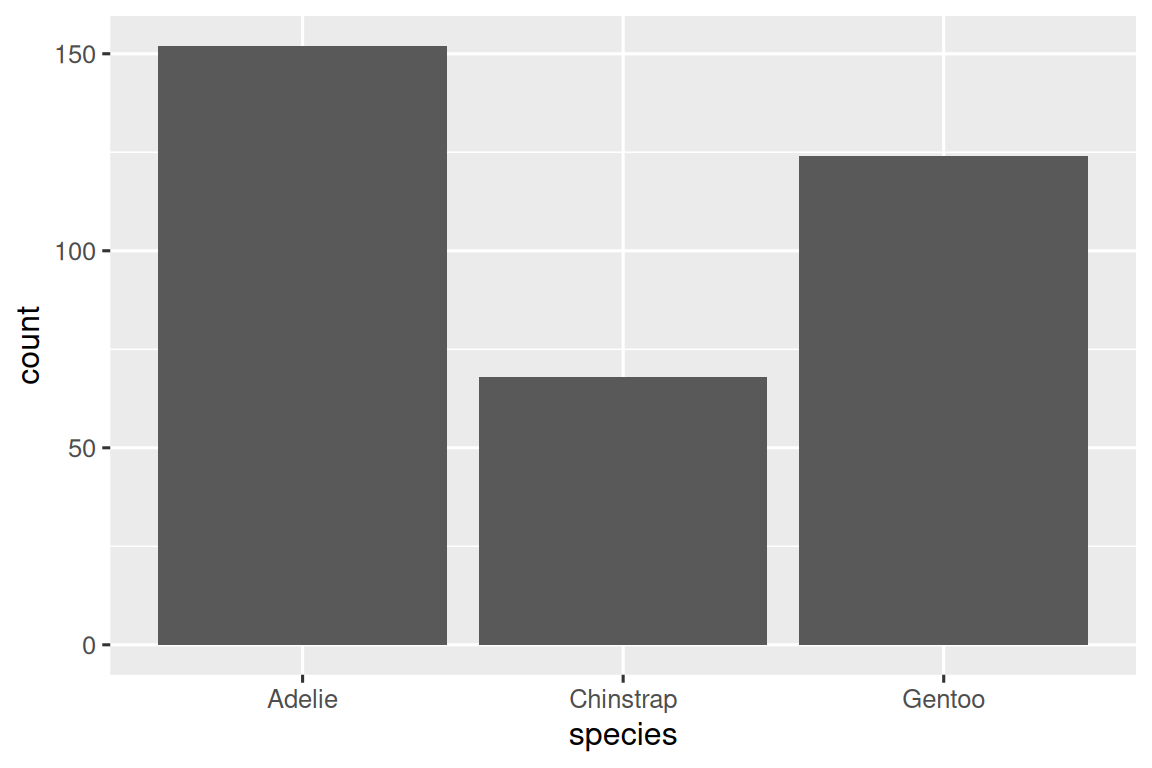
在具有無序級別的分類變量的條形圖中，例如上面的企鵝物種（species），通常最好根據它們的頻率重新排序條形。為此，需要將變量轉換為因子（factor）（R 如何處理分類數據），然后重新排序該因子的級別（levels）。

ggplot(penguins,?aes(x?=?fct_infreq(species)))?+geom_bar()

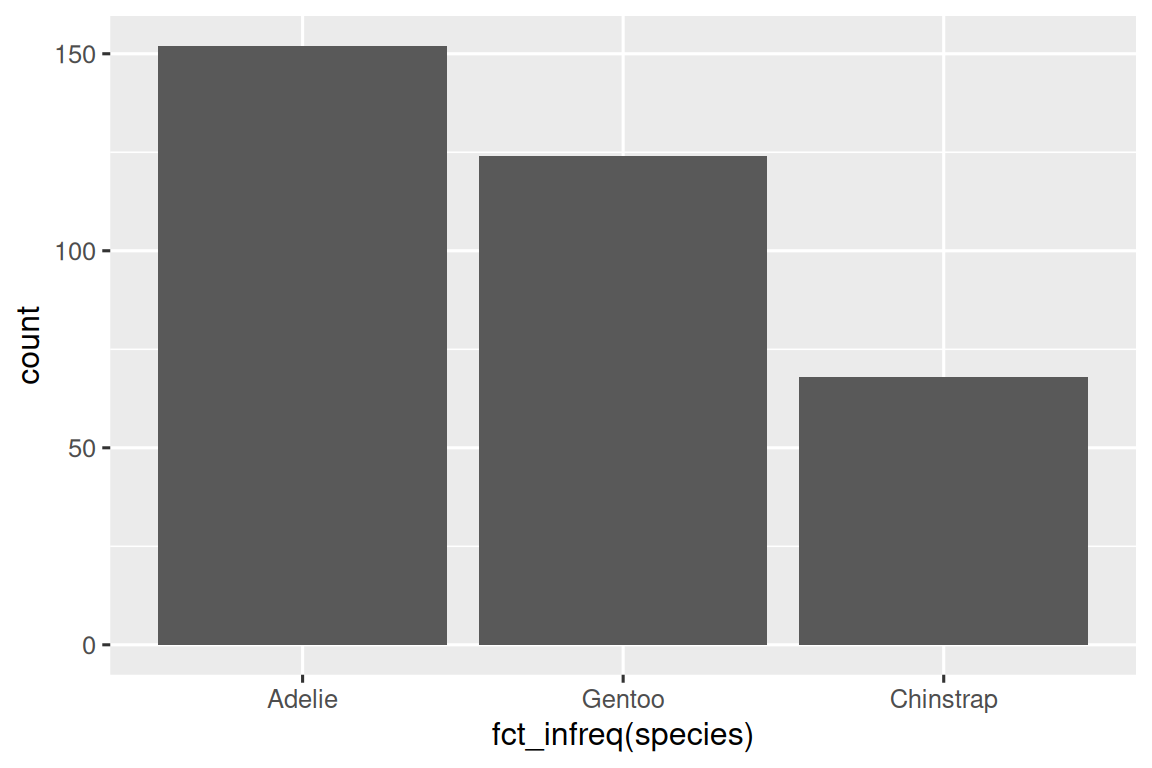
您將在 Chapter 16 中進一步了解有關因子（factors）和處理因子的函數（如上面所示的 fct_infreq()）的知識。

1.4.2 一個數值變量

如果一個變量可以取一系列廣泛的數值，并且可以對這些數值進行加減或求平均，那么該變量就是數值變量（numerical）。數值變量可以是連續的（continuous）或離散的（discrete）。

直方圖（histogram）是一種常用的連續變量分布可視化方法。

ggplot(penguins,?aes(x?=?body_mass_g))?+geom_histogram(binwidth?=?200)

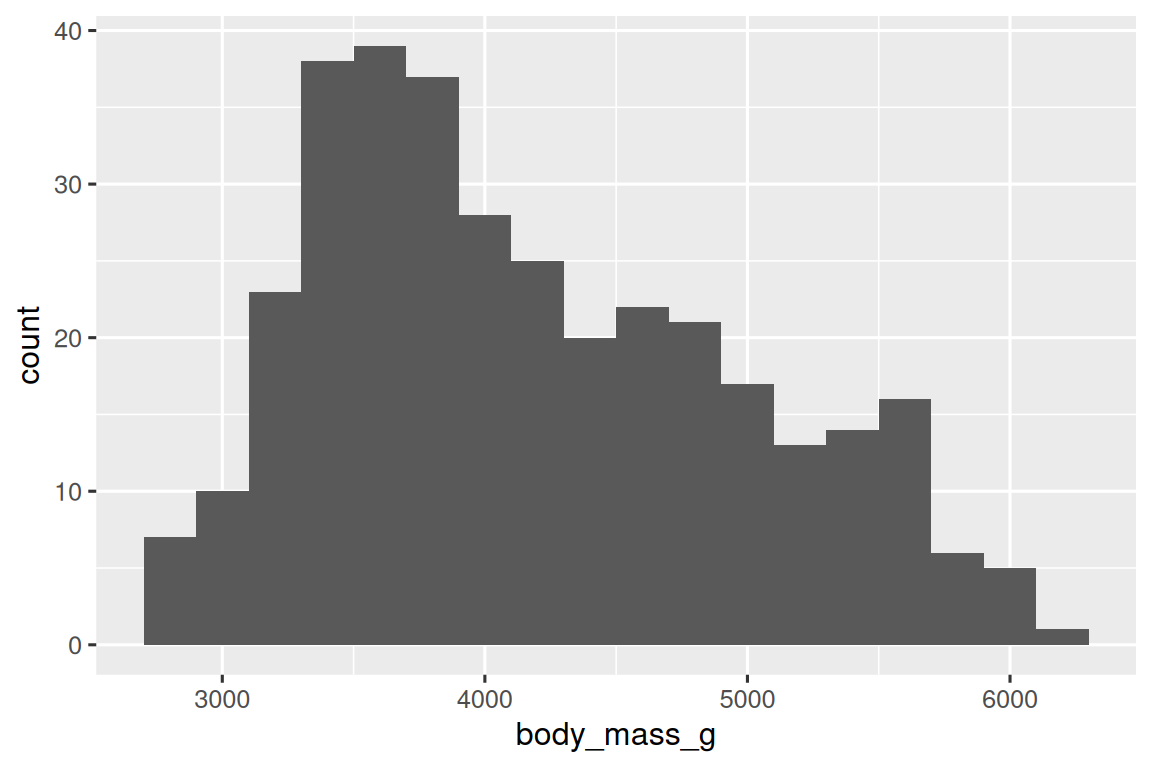
直方圖將 x-axis 均勻地分成多個區間（bins），并使用條的高度顯示落入每個區間的觀測次數。在上面的圖中，最高的條表示有 39 個觀測值的 body_mass_g 值介于 3,500 到 3,700 克之間，這個區間是條的左右邊緣。

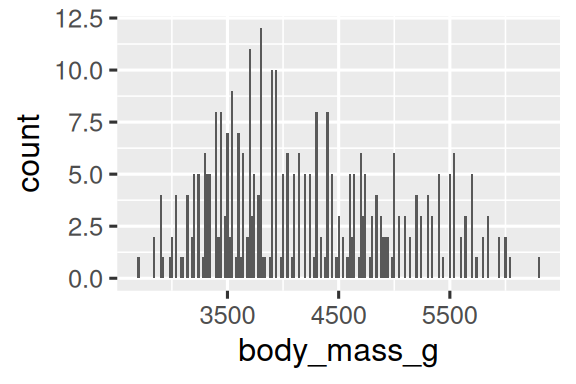
您可以使用 binwidth 參數設置直方圖中的區間寬度，該參數以 x 變量的單位進行測量。在使用直方圖時，應該嘗試不同的區間寬度，因為不同的區間寬度可以展現不同的模式。在下面的圖中，區間寬度為 20 太窄了，導致有太多的條，使得難以確定分布的形狀。類似地，區間寬度為 2,000 太大了，導致所有的數據都被分到了只有三個條中，也難以確定分布的形狀。區間寬度為 200 提供了一個合理的平衡點。

ggplot(penguins,?aes(x?=?body_mass_g))?+geom_histogram(binwidth?=?20)
ggplot(penguins,?aes(x?=?body_mass_g))?+geom_histogram(binwidth?=?2000)

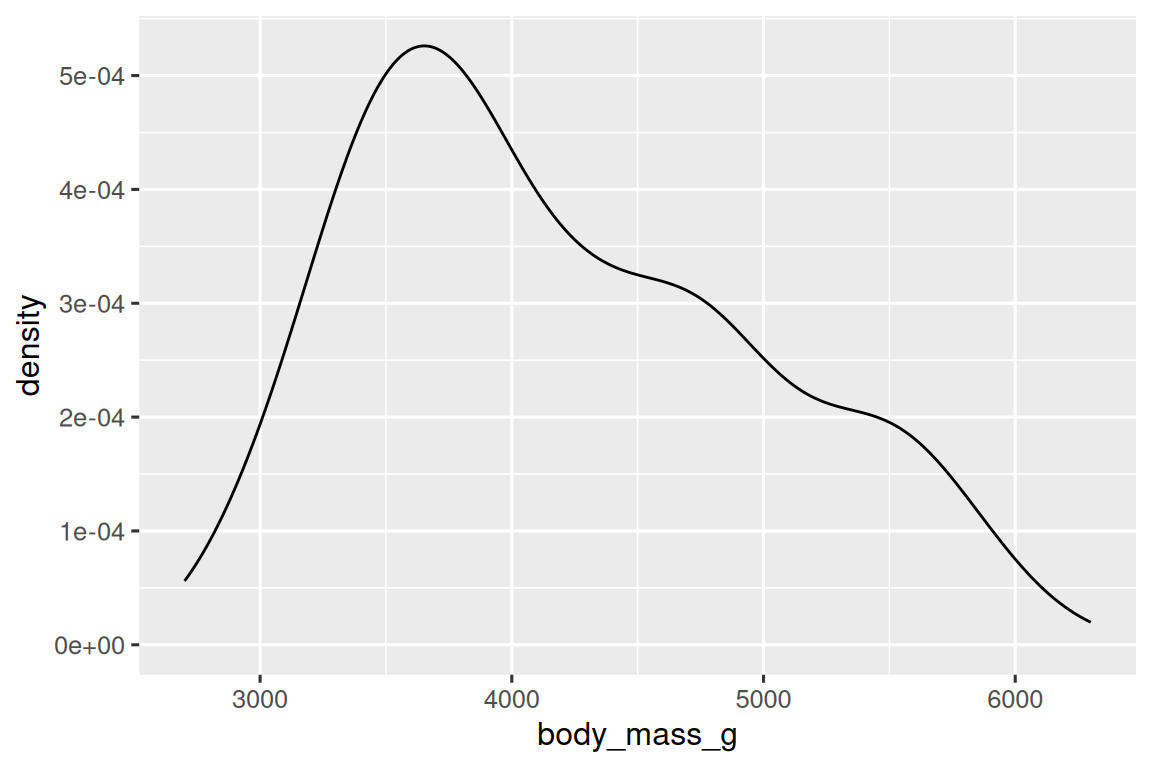
一種用于可視化數值變量分布的替代方法是密度圖（density plot）。密度圖是直方圖的平滑版本，特別適用于連續數據，這些數據來自于一個平滑分布。我們不會詳細討論 geom_density() 如何估計密度（您可以在函數文檔中相關信息），但我們可以通過類比來解釋繪制密度曲線的過程。想象一個由木塊組成的直方圖。然后，想象一根煮熟的意大利面條放在上面。面條垂掛在木塊上的形狀可以被視為密度曲線的形狀。它展示的細節比直方圖少，但可以更容易地快速了解分布的形狀，特別是關于峰值和偏斜度方面的特征。

ggplot(penguins,?aes(x?=?body_mass_g))?+geom_density()
#>?Warning:?Removed?2?rows?containing?non-finite?outside?the?scale?range
#>?(`stat_density()`).

1.4.3 練習

創建一個關于 penguins 數據集中的 species 變量的條形圖（bar plot），將 species 分配給 y aesthetic。這個圖與之前的圖有何不同？
下面兩個圖形有何不同？color 和 fill 這兩個美學映射中，哪一個更適合改變條形圖的顏色？

ggplot(penguins,?aes(x?=?species))?+geom_bar(color?=?"red")ggplot(penguins,?aes(x?=?species))?+geom_bar(fill?=?"red")

geom_histogram() 中的 bins 參數有什么作用？
在加載 tidyverse 包時，可以使用 diamonds 數據集中的 carat 變量創建一個直方圖（histogram）。嘗試使用不同的區間寬度（binwidths）來觀察結果。哪個區間寬度（binwidths）可以顯示出最有趣的模式？

1.5 可視化關系圖

要可視化一個關系（relationship），我們至少需要將兩個變量映射到繪圖的 aesthetics 中。在接下來的章節中，您將學習常用的用于可視化兩個或多個變量之間關系的圖表以及用于創建這些圖表的幾何對象（geoms）。

1.5.1 一個數值和一個分類變量

要可視化數值變量和分類變量之間的關系，我們可以使用并列箱線圖。箱線圖（boxplot）是一種用于描述分布位置（百分位數）的視覺工具。它還可以用于識別潛在的異常值（outliers）。如 Figure 1.1 所示，每個箱線圖由以下幾部分組成：

一個 box，用于表示數據的中間一半的范圍，也就是四分位距（IQR），從分布的第 25 個百分位數延伸到第 75 個百分位數。box 的中間有一條線，顯示分布的中位數，即第 50 個百分位數。這三條線可以讓您了解分布的擴展程度以及分布是否關于中位數對稱或傾斜于一側。
用于顯示位于 box 邊緣 1.5 倍 IQR 之外的觀測值的可視化點。這些異常點是不尋常的，因此會單獨繪制出來。
從 box 的每一端延伸出一條線（或者稱為 whisker），并延伸到分布中最遠的非異常點。

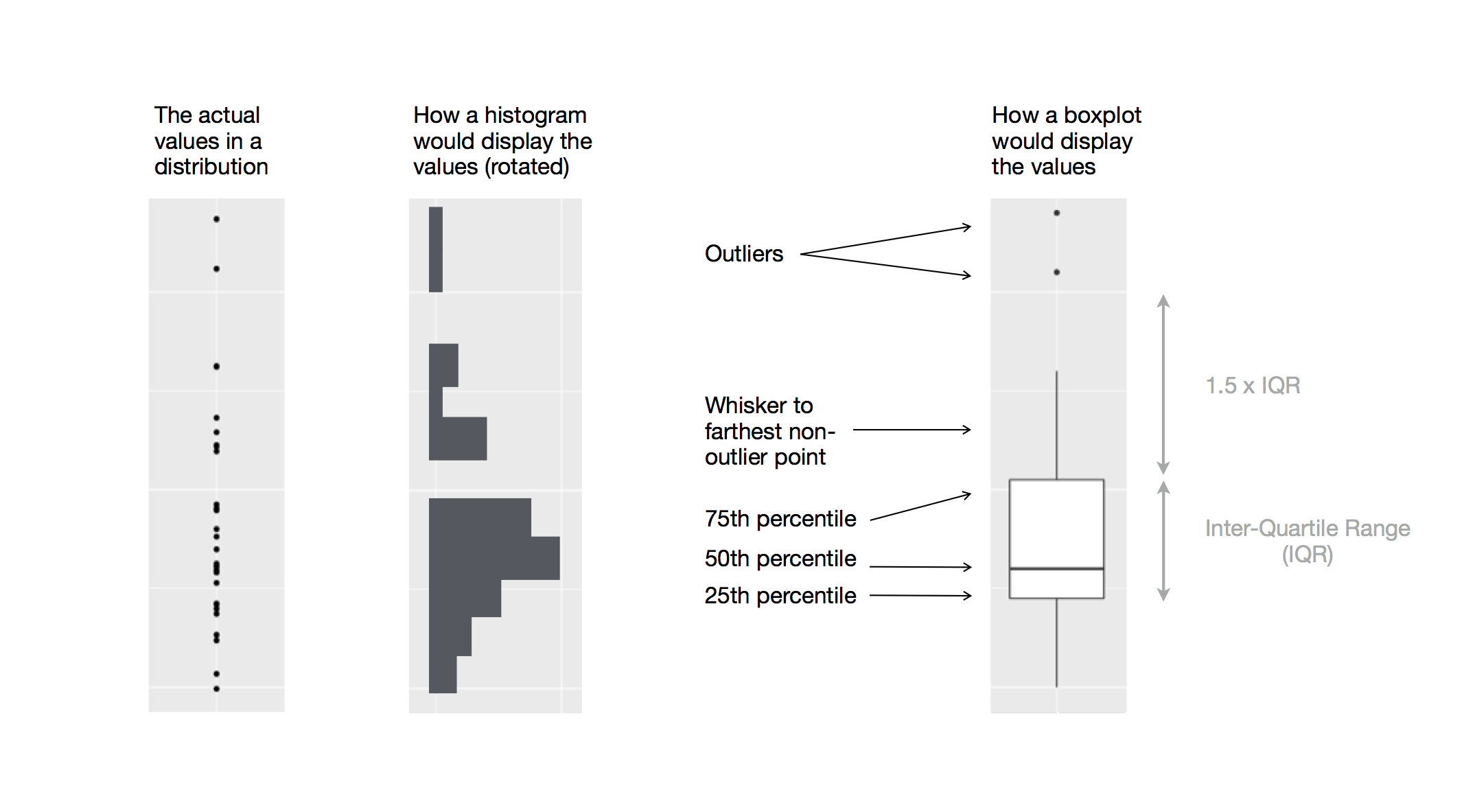
Figure 1.1: 圖表描繪了如何創建箱線圖。

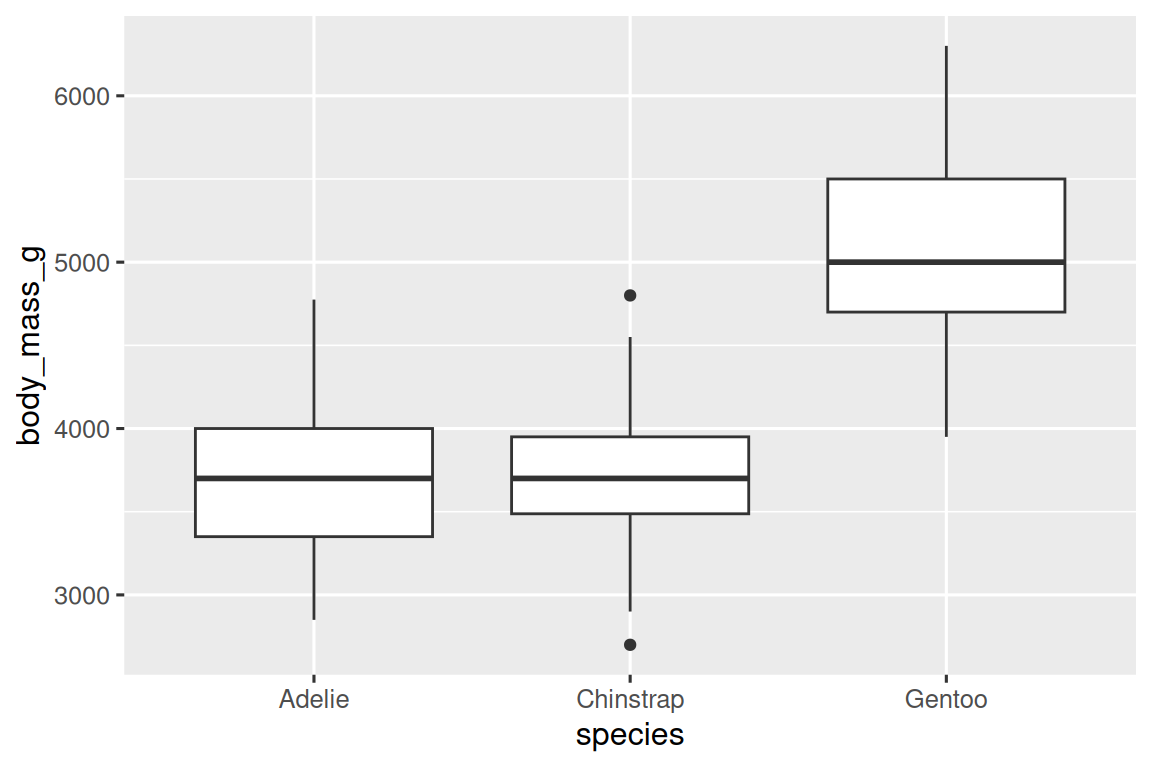
讓我們使用 geom_boxplot() 來查看不同物種（species）的體重（body mass）分布：

ggplot(penguins,?aes(x?=?species,?y?=?body_mass_g))?+geom_boxplot()

或者，我們可以使用 geom_density() 創建密度圖（density plots）。

ggplot(penguins,?aes(x?=?body_mass_g,?color?=?species))?+geom_density(linewidth?=?0.75)

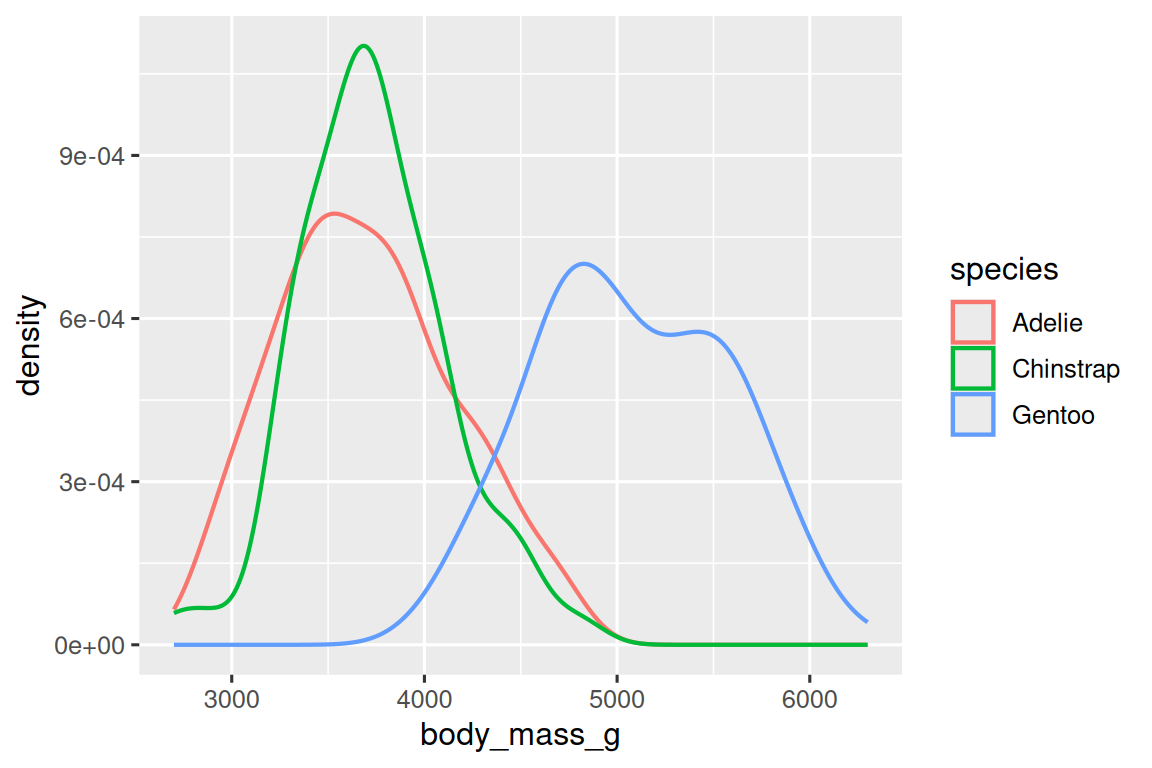
我們還使用 linewidth 參數自定義了線條的粗細，以使其在背景中更加突出。

此外，我們可以將 species 映射到 color 和 fill aesthetics，并使用 alpha aesthetic 為填充的密度曲線添加透明度。這個 aesthetic 的取值范圍在 0（完全透明）和 1（完全不透明）之間。在下面的圖中，它被設置為 0.5。

ggplot(penguins,?aes(x?=?body_mass_g,?color?=?species,?fill?=?species))?+geom_density(alpha?=?0.5)

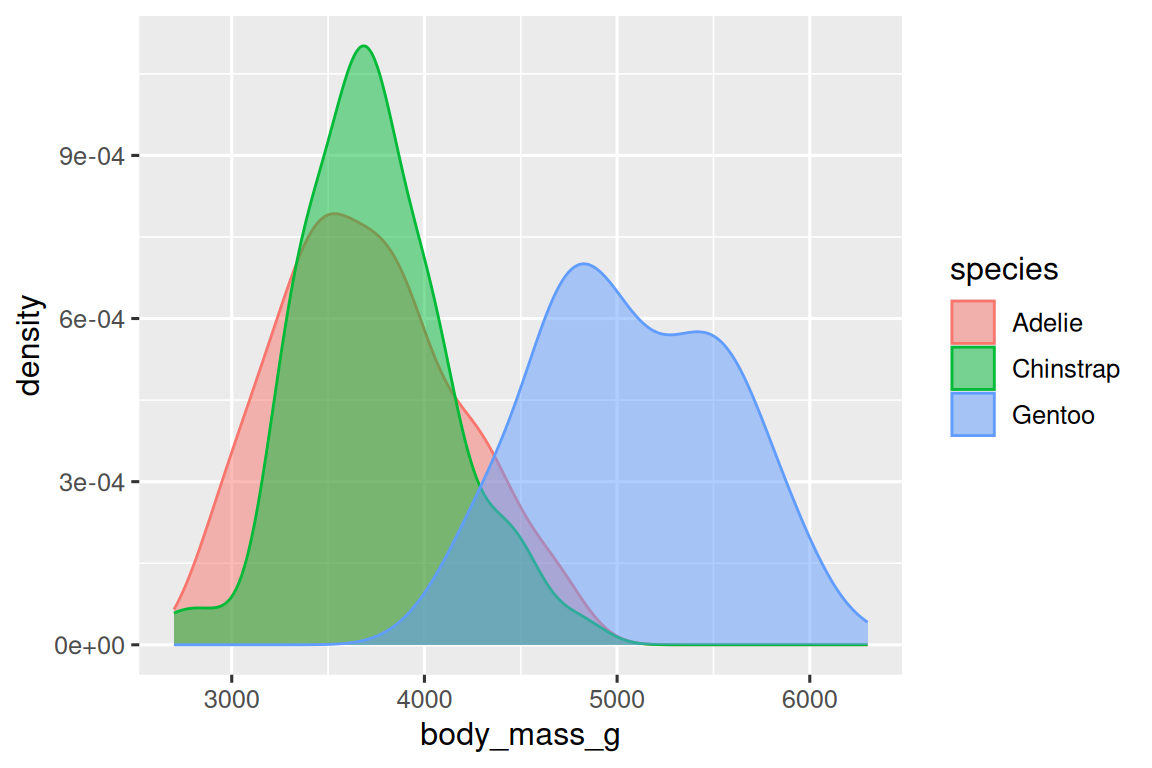
請注意我們在這里使用的術語：

如果我們希望由變量的值決定該美學屬性的視覺特征的變化，我們會將變量映射（map）到美學屬性。
否則，我們會設置（set）美學屬性的值。

1.5.2 兩個分類變量

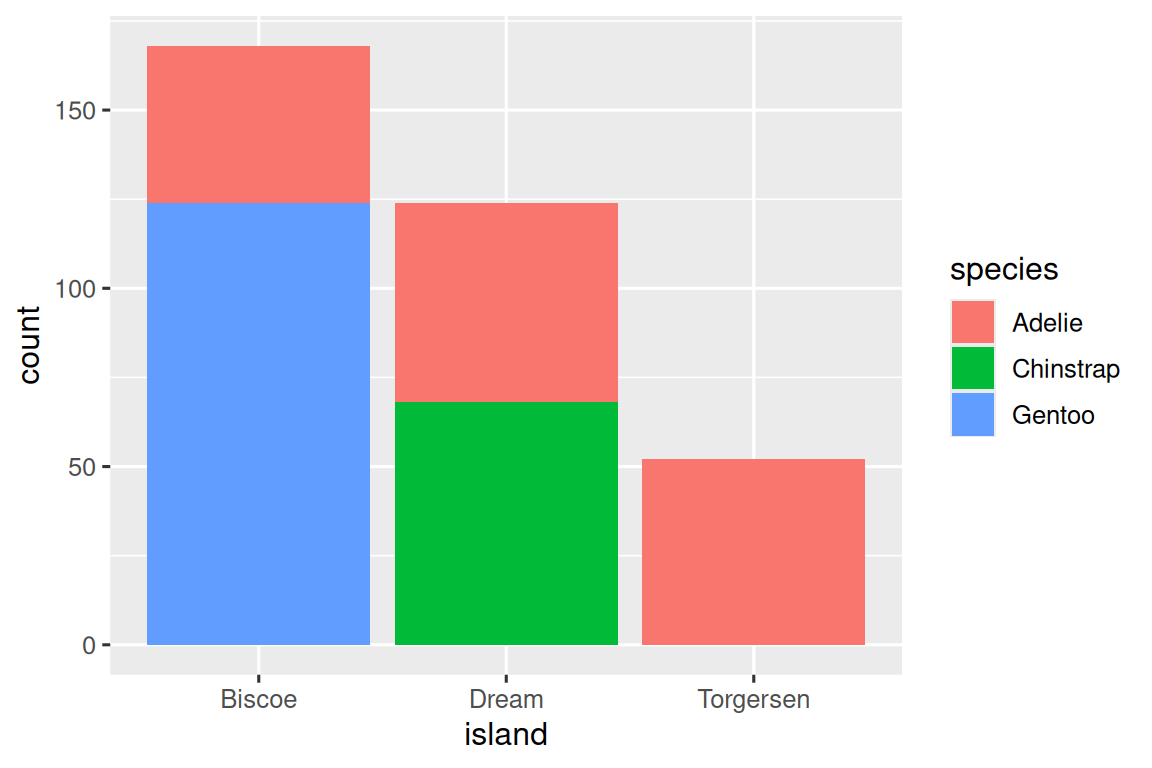
我們可以使用堆疊條形圖（stacked bar plots）來可視化兩個分類變量之間的關系。例如，以下兩個堆疊條形圖都顯示了 island 和 species 之間的關系，具體而言，可視化了每個島上 species 的分布。

第一個圖顯示了每個島上各種企鵝物種的頻率。頻率圖顯示在每個島上，Adelie 的數量是相等的。但我們無法很好地了解每個島內的百分比分布情況。

ggplot(penguins,?aes(x?=?island,?fill?=?species))?+geom_bar()

第二個圖是一個相對頻率圖，通過在 geom 中設置 position = "fill" 創建，它對比較跨島嶼的物種分布更有用，因為它不受島嶼上企鵝數量不均衡的影響。使用這個圖表，我們可以看到 Gentoo 企鵝全部生活在 Biscoe 島上，并占該島企鵝總數的大約 75％，Chinstrap 企鵝全部生活在 Dream 島上，并占該島企鵝總數的大約 50％，而 Adelie 企鵝分布在所有三個島嶼上，并占據 Torgersen 島上所有的企鵝。

ggplot(penguins,?aes(x?=?island,?fill?=?species))?+geom_bar(position?=?"fill")

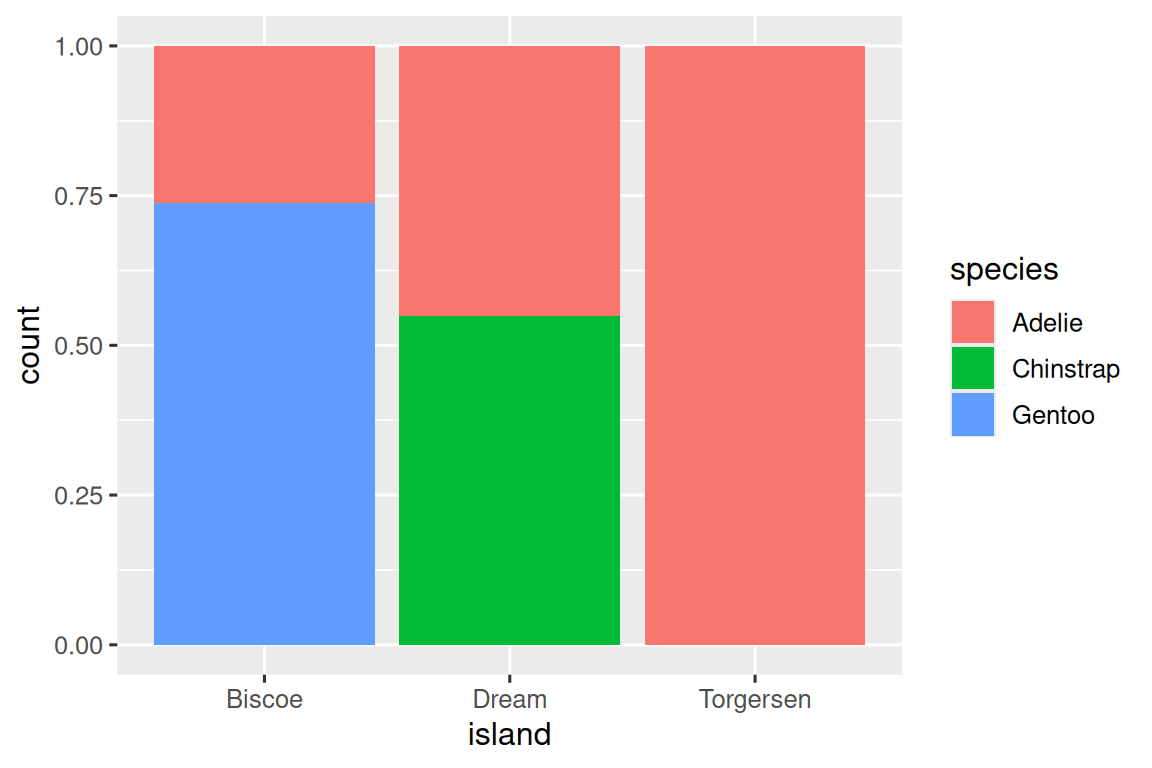
在創建這些條形圖時，我們將要分隔成條的變量映射到 x aesthetic，將用于改變條內顏色的變量映射到 fill aesthetic。

1.5.3 兩個數值變量

到目前為止，你已經學習了使用 geom_point() 創建散點圖和使用 geom_smooth() 創建平滑曲線來可視化兩個數值變量之間的關系。散點圖可能是最常用的用于可視化兩個數值變量之間關系的圖表之一。

ggplot(penguins,?aes(x?=?flipper_length_mm,?y?=?body_mass_g))?+geom_point()

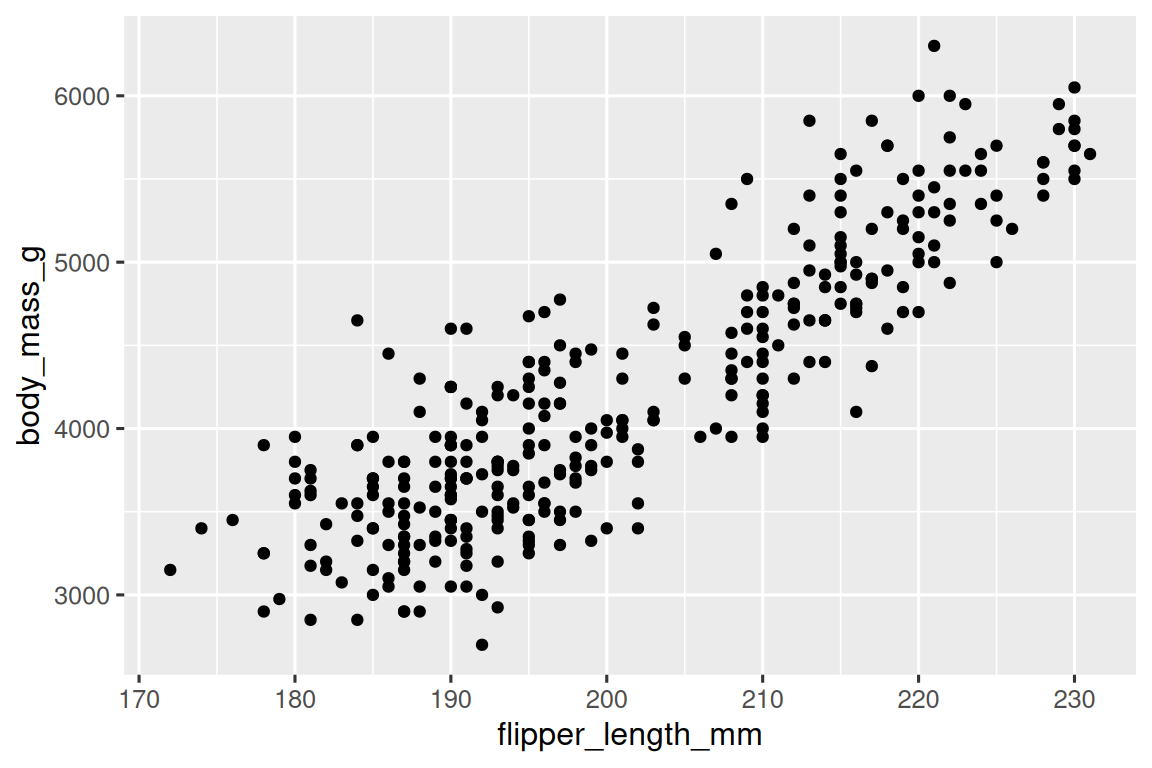
1.5.4 三個或更多變量

正如我們在 Section 1.2.4 中所看到的，我們可以通過將它們 mapping 到其他 aesthetics 來將更多變量融入到圖表中。例如，在下面的散點圖中，點的顏色代表物種（species），點的形狀代表島嶼（islands）。

ggplot(penguins,?aes(x?=?flipper_length_mm,?y?=?body_mass_g))?+geom_point(aes(color?=?species,?shape?=?island))

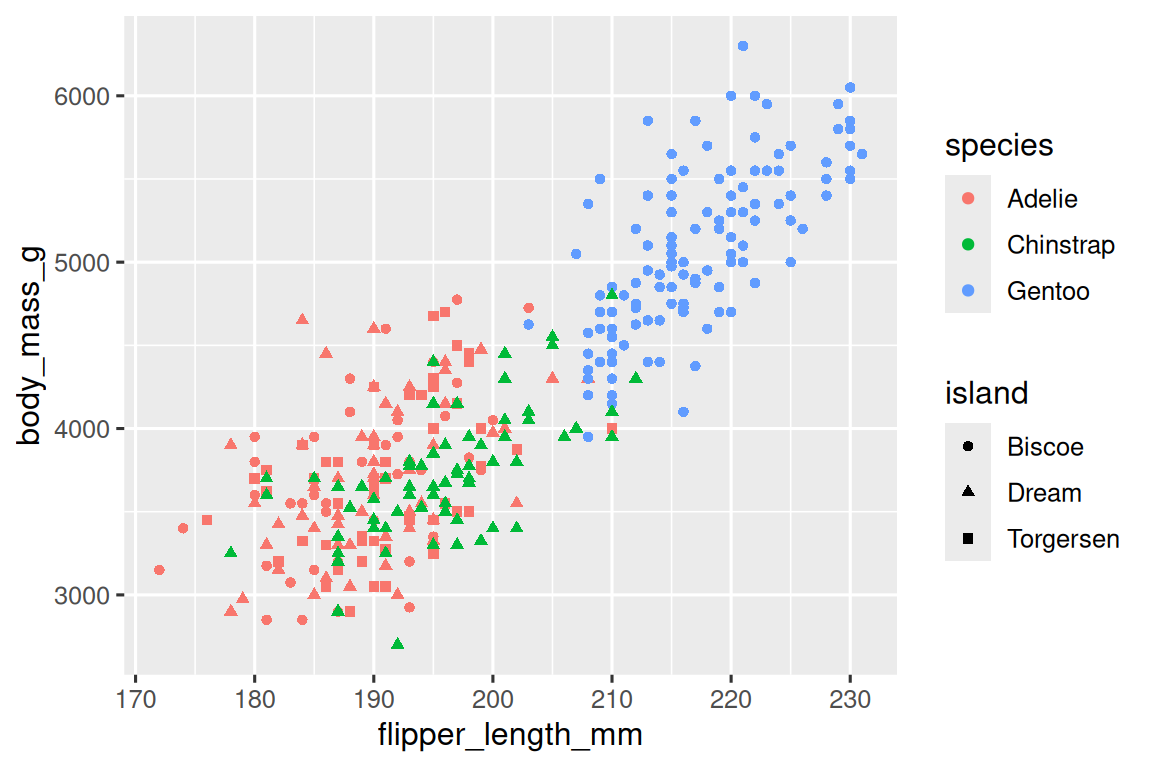
然而，如果將過多的 aesthetic mappings 添加到圖表中，會使其變得雜亂且難以理解。另一種方法，特別適用于分類變量，是將圖表分割為面板（facets），每個面板顯示數據的一個子集。

要通過單個變量進行面板化，可以使用 facet_wrap() 函數。facet_wrap() 的第一個參數是一個公式，可以使用 ~ 后跟一個變量名來創建。傳遞給 facet_wrap() 的變量應該是分類變量。

ggplot(penguins,?aes(x?=?flipper_length_mm,?y?=?body_mass_g))?+geom_point(aes(color?=?species,?shape?=?species))?+facet_wrap(~island)

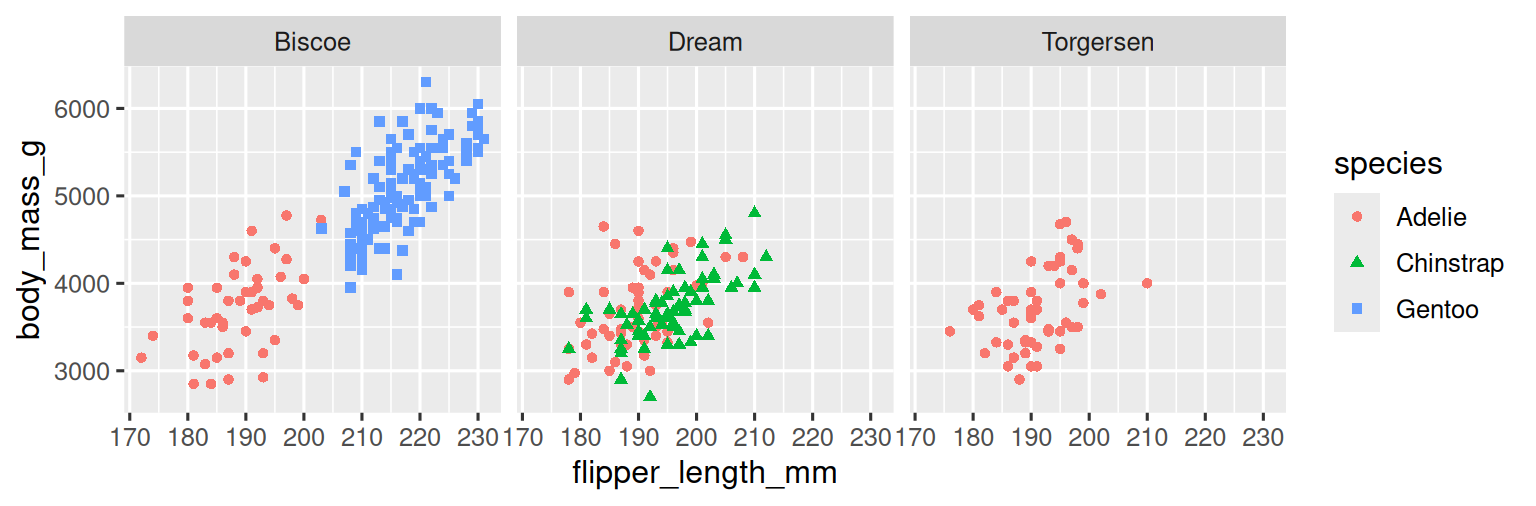
您將在 Chapter 9 中學習到許多其他用于可視化變量分布和它們之間關系的幾何對象（geoms）。

1.5.5 練習

根據 ggplot2 軟件包中捆綁的 mpg 數據框，該數據框包含了美國環境保護署收集的 234 個觀測數據，涵蓋了 38 個汽車型號。在 mpg 數據框中，哪些變量是分類變量？哪些變量是數值變量？（提示：輸入 ?mpg 來閱讀數據集的文檔。）當您運行 ?mpg 時，如何查看這些信息？
使用 mpg 數據框創建一個 hwy vs. displ 的散點圖。然后，將第三個數值變量映射到 color、size、color 和 size 以及 shape。這些 aesthetics 在分類變量和數值變量上的行為有何不同？
在 hwy vs. displ 的散點圖中，如果將第三個變量映射到 linewidth 會發生什么？
如果將同一個變量映射到多個 aesthetics 會發生什么？
創建一個 bill_depth_mm vs. bill_length_mm 的散點圖，并按照 species 對點進行著色。將點按物種（species）著色有關于這兩個變量之間關系的什么信息？通過對物種（species）進行分面繪圖（faceting）又會發現什么？
為什么下面的代碼會產生兩個獨立的圖例（legends）？如何修復它以合并這兩個圖例？

ggplot(data?=?penguins,mapping?=?aes(x?=?bill_length_mm,?y?=?bill_depth_mm,?color?=?species,?shape?=?species)
)?+geom_point()?+labs(color?=?"Species")

創建下面的兩個堆疊條形圖。第一個圖可以回答哪個問題？第二個圖可以回答哪個問題？

ggplot(penguins,?aes(x?=?island,?fill?=?species))?+geom_bar(position?=?"fill")
ggplot(penguins,?aes(x?=?species,?fill?=?island))?+geom_bar(position?=?"fill")

1.6 保存你的繪圖

一旦你創建了一個圖形，你可能希望將其保存為圖像文件以在其他地方使用。這時可以使用 ggsave() 函數來將最近創建的圖形保存到磁盤中：

ggplot(penguins,?aes(x?=?flipper_length_mm,?y?=?body_mass_g))?+geom_point()
ggsave(filename?=?"penguin-plot.png")

這將把你的圖形保存到你的工作目錄中，你會在 Chapter 6 中更詳細地了解到這個概念。

如果你沒有指定 width 和 height 參數，它們將從當前繪圖設備的尺寸中獲取。為了獲得可重現的代碼，建議你指定這些參數。你可以在文檔中了解更多關于 ggsave() 函數的信息。

然而，通常我們建議使用 Quarto 來組織最終的報告。Quarto 是一個可重復使用的創作系統，允許你將代碼和文字交織在一起，并自動將圖形包含在你的寫作中。你將在 Chapter 28 中了解更多關于 Quarto 的內容。

1.6.1 練習

運行以下代碼行。兩個圖中的哪一個保存為 mpg-plot.png？為什么？

ggplot(mpg,?aes(x?=?class))?+geom_bar()
ggplot(mpg,?aes(x?=?cty,?y?=?hwy))?+geom_point()
ggsave("mpg-plot.png")

您需要在上面的代碼中更改什么才能將繪圖保存為 PDF 而不是 PNG？你如何找出哪些類型的圖像文件可以在 ggsave() 中工作？

1.7 常見問題

當您開始運行 R 代碼時，可能會遇到一些問題。不要擔心，這種情況對每個人都會發生。我們多年來一直在編寫 R 代碼，但每天我們仍然會寫出一開始就無法正常工作的代碼！

首先，仔細比較您正在運行的代碼與書中的代碼。R 非常挑剔，一個錯位的字符可能會產生完全不同的結果。確保每個 ( 都與一個 ) 匹配，每個 " 都與另一個 " 配對。有時候您運行代碼后什么都沒有發生。檢查您控制臺的左側：如果是 +，這意味著 R 認為您輸入的不是完整的表達式，它正在等待您完成。在這種情況下，通常通過按 ESCAPE 鍵中止處理當前命令，然后重新開始會比較容易。

在創建 ggplot2 圖形時，一個常見的問題是將 + 放在錯誤的位置：它必須放在行尾，而不是行首。換句話說，請確保您沒有意外地編寫了以下這種代碼：

ggplot(data?=?mpg)?
+?geom_point(mapping?=?aes(x?=?displ,?y?=?hwy))

如果您仍然遇到困難，請嘗試獲取幫助。您可以在控制臺中運行 ?function_name 來獲取有關任何 R 函數的幫助，或者在 RStudio 中選中函數名并按下 F1 鍵。如果幫助信息似乎不太有用，不要擔心，可以跳到示例部分，尋找與您嘗試做的事情相匹配的代碼示例。

如果這樣還無法解決問題，請仔細閱讀錯誤消息。有時候答案就埋在錯誤消息中！但是，當您剛開始接觸 R 時，即使答案在錯誤消息中，您可能還不知道如何理解它。另一個很好的工具是 Google：嘗試搜索錯誤消息，因為很可能有其他人遇到了同樣的問題，并在網上尋求了幫助。

1.8 總結

在本章中，您學習了使用 ggplot2 進行數據可視化的基礎知識。我們從支持 ggplot2 的基本思想開始：可視化是從數據中的變量到 aesthetic（如 position、color、size、shape）的 mapping。然后，您逐層學習了如何增加復雜性并改進繪圖的呈現方式。您還學習了用于可視化單個變量分布以及可視化兩個或多個變量之間關系的常用圖表，通過使用附加的 aesthetic mappings 和/或使用 faceting 將繪圖分割為小多面體進行繪制。

在本書的后續部分，我們將一次又一次地使用可視化，根據需要引入新的技術，并在 Chapter 9 到 Chapter11 中深入探討如何使用 ggplot2 創建可視化。

在掌握了可視化的基礎知識之后，在下一章中，我們將轉換一下思路，為您提供一些實際的工作流程建議。我們將在本書的這一部分中穿插工作流程建議和數據科學工具，因為這將幫助您在編寫越來越多的 R 代碼時保持組織性。

您可以使用 conflicted 包來消除該消息，并在需要時強制進行沖突解決。隨著加載更多的包，這變得更為重要。您可以在 https://conflicted.r-lib.org 了解更多關于 conflicted 的信息。
Horst AM, Hill AP, Gorman KB (2020). palmerpenguins: Palmer Archipelago (Antarctica) penguin data. R package version 0.1.0. https://allisonhorst.github.io/palmerpenguins/. doi: 10.5281/zenodo.3960218.
在這里，"formula" 是 ~ 創建的事物的名稱，而不是 "equation" 的同義詞。

--------------- 本章結束 ---------------

本期翻譯貢獻：