目錄

1.直接選擇排序

1.1直接選擇排序的思想

1.2直接選擇排序的代碼邏輯

1.3完整排序代碼

1.3.1一次只選一個最值

1.3.2一次篩選出兩個最值

1.4直接選擇排序的時間復雜度與空間復雜度

2.堆排序

2.1堆排序的思想

2.2堆排序的具體步驟

2.3堆排序圖解

2.4完整排序代碼

3.冒泡排序

3.1冒泡排序的思想

3.2冒泡排序圖解

3.3單趟排序代碼(一輪遍歷進行的操作)?

3.4完整排序代碼

3.5冒泡排序的時間復雜度與空間復雜度

---

所有排序的實現皆以升序為例

1.直接選擇排序

1.1直接選擇排序的思想

直接選擇排序的思想就是對數組進行多輪遍歷，在每一輪遍歷中，從當前未排序部分的元素里選出最大值或最小值，然后依據排序要求，將該最大值或最小值與未排序部分的起始位置或末尾位置的元素進行交換，從而逐步確定數組中各元素的最終位置，最終實現數組有序

1.2直接選擇排序的代碼邏輯

就是根據思想：遍歷+篩選

1.3完整排序代碼

1.3.1一次只選一個最值

void SelectSortUp1(int* a, int n){for(int j = 0; j < n - 1; ++j){int min = j;for (int i = j + 1; i < n; ++i){if (a[i] < a[min])min = i;}Swap(&a[j], &a[min]);}
}

以升序為例，一次遍歷(對未排序部分的遍歷)選出的最小值放在未排序部分的起始位置

內層循環進行的是特定的某一次遍歷的篩選過程

外層循環控制了每次遍歷時的起始位置以及交換過程

1.3.2一次篩選出兩個最值

void SelectSortUp2(int* a, int n){int left = 0, right = n - 1;while(left < right){int min = left, max = left;for (int i = left + 1; i <= right; ++i){if (a[i] < a[min])min = i;if (a[i] > a[max])max = i;}Swap(&a[min], &a[left]);if (left == max)max = min;Swap(&a[max], &a[right]);++left;--right;}
}

對思想進行精進，一次遍歷，選出未排序部分的最大和最小值，按需將其放在對應位置

left、right 控制的是未排序部分的區間大小

一次遍歷選出最大最小值后，以升序為例，

最小值放在未排序部分的起始位置，最大值放在未排序部分的末尾

然后縮小區間

1.4直接選擇排序的時間復雜度與空間復雜度

假設數組有N個元素，一次只選出一個最值，則最壞情況下，第一輪遍歷需遍歷N個元素，第二輪遍歷序遍歷N-1個元素.............第N-1輪遍歷需遍歷2個元素，遍歷結束，遍歷次數為((N+2)*(N-1))/2

所以時間復雜度為O(N^2)

一次篩選出兩個最值，則最壞情況下，第一輪遍歷大約需遍歷N個元素，第二輪遍歷需遍歷N-2個元素.............一共約遍歷N/2輪，遍歷次數為 ((2+N)*N）/ 2，時間復雜度為O(N^2）

直接選擇排序的變量個數固定，所有操作均在原數組上，所以空間復雜度為O(1)?

2.堆排序

關于堆，可參考前兩期博客? 數據結構 之 【堆】、堆的應用

2.1堆排序的思想

數組可以模擬完全二叉樹，堆是一種完全二叉樹，且具備選數的功能，那么

將數組持續變為堆，并對特定的堆選出最值，最終可實現數組有序

2.2堆排序的具體步驟

1.建堆：按需將所給數組變為大(小)堆? ? (建堆的具體步驟參考? 堆的應用 這一期博客)

升序建大堆，降序建小堆

2.交換與調整：以升序為例，建成大堆后，將堆頂元素(為未排序部分的最大值)與末尾位置的元素進行交換，然后對末尾位置之前的所有元素進行向下調整操作，使其再次成為大堆，然后交換堆頂元素與未排序部分的末尾位置的元素，........循環進行調整與交換操作，直到未排序部分的元素個數為1為止

2.3堆排序圖解

2.4完整排序代碼

void AdjustDown(HpDateType* a, int n, int parent){int child = parent * 2 + 1;//有左孩子才進行調整while (child < n)//n是節點個數{//左孩子一個邏輯，右孩子一個邏輯，直接假設//child是左右孩子中較大的一個孩子的下標//注意右孩子的有無(防止越界訪問與無效數據)if (child + 1 < n && a[child] < a[child + 1]){++child;}//與左右孩子中較大的一個孩子進行比較if (a[parent] < a[child]){Swap(&a[parent], &a[child]);parent = child;child = parent * 2 + 1;}else    break;}
}
void HeapSortUp(int* a, int n){//從第一個非葉子節點開始建堆for (int i = (n - 2) / 2; i >= 0; --i){AdjustDwon1(a, n, i);}//堆頂元素與末尾交換，并向下調整//顯然是循環int end = n - 1;while (end > 0){Swap(&a[0], &a[end]);AdjustDwon1(a, end, 0);--end;}
}

通過逐步縮小堆的范圍來排序數組

當堆中只剩一個元素時（即?end = 0），排序過程已完成，?所以 end > 0 作為循環結束條件

2.5堆排序的時間復雜度與空間復雜度

堆排序的時間復雜度O(N*logN)，可用最壞情況下的交換次數進行衡量

空間復雜度為O(1)

3.冒泡排序

3.1冒泡排序的思想

進行多輪遍歷，每輪遍歷中，依次比較相鄰元素，若不符合目標順序（升序則前大后小，降序則前小后大），就交換它們的位置。如此，每輪遍歷會將當前未排序部分的最大（小）值“冒泡”到數組一端。當某一輪遍歷無元素交換時，排序完成

3.2冒泡排序圖解

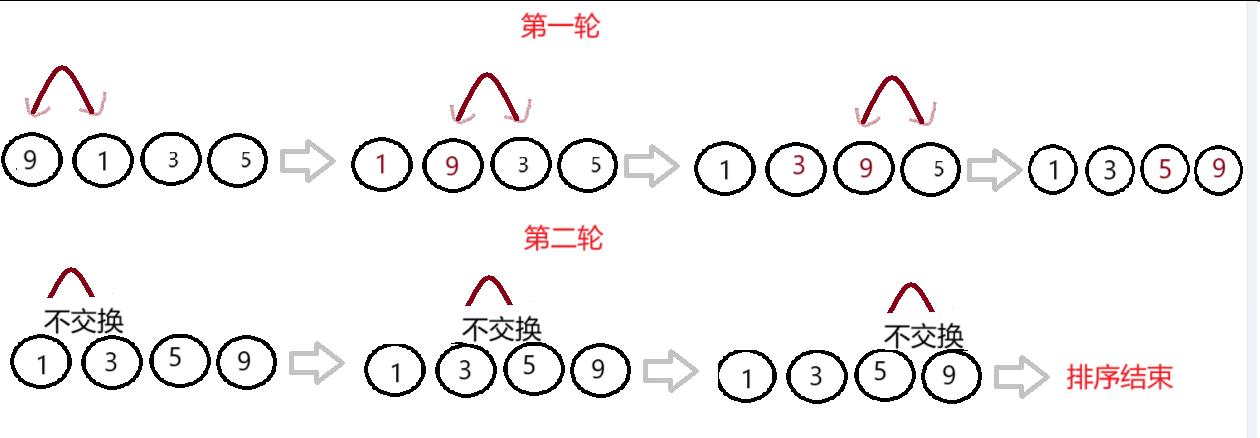
3.3單趟排序代碼(一輪遍歷進行的操作)?

for (int j = 0; j < n - 1; ++j){if (a[j] > a[j + 1]){Swap(&a[j], &a[j + 1]);}
}

上述代碼展示的是第一次遍歷進行的操作，數組元素兩兩進行比較，j + 1 < n，所以 j < n - 1

因為是升序，前一個數比后一個數大就交換

3.4完整排序代碼

void BubbleSortUp(int* a, int n){//一趟只正確放好一個數//n個數n - 1 趟for(int i = 0; i < n - 1; ++i){//經過一趟少一次比較for (int j = 0; j < n - 1 - i; ++j){if (a[j] > a[j + 1]){Swap(&a[j], &a[j + 1]);}}}
}

冒泡排序遍歷一輪可正確放好一個數組元素，則有n個數組元素的數組只需遍歷n-1輪

冒泡排序遍歷一輪可正確放好一個數組元素，那么遍歷一輪可減少一次比較次數

小優化

內層循環未進行交換操作則證明數組有序，此時可終止循環，減少不必要的循環操作

void BubbleSortUp(int* a, int n){//一趟只正確放好一個數//n個數n - 1 趟for(int i = 0; i < n - 1; ++i){int flag = 0;//經過一趟少一次比較for (int j = 0; j < n - 1 - i; ++j){if (a[j] > a[j + 1]){Swap(&a[j], &a[j + 1]);flag = 1;}}if (!flag)break;}
}

3.5冒泡排序的時間復雜度與空間復雜度

?假設數組有N個元素，則最壞情況下，第一輪遍歷需交換N-1次，第二輪遍歷需交換N-2次，

.............第N-1輪遍歷需交換1次，交換總次數為 ((N-1)*N) / 2， 時間復雜度為O(N^2)

變量個數固定，所有操作均在原數組上，空間復雜度為O(1)?