探索VB.NET中的貝塞爾Bezier曲線繪制技巧

簡介：Bezier曲線是計算機圖形學中用于創建平滑曲線的重要工具，廣泛應用于圖形設計、游戲開發、CAD系統等領域。本文深入探討了Bezier曲線的基礎知識，并詳細說明了如何在Visual Basic中使用?Graphics?對象的?DrawBezier?方法繪制曲線。通過理論學習和實踐操作，讀者將掌握調整控制點以實現曲線平滑的技巧，增強在圖形編程方面的能力。?

1. Bezier曲線概念與應用

在現代計算機圖形學中，Bezier曲線作為一項基礎且強大的工具，在各個領域中扮演著極其重要的角色。不論是網頁設計、圖形設計、游戲開發還是CAD系統，Bezier曲線都以其實現路徑平滑、形狀編輯簡便的特點獲得了廣泛的應用。簡單來說，Bezier曲線是一種通過控制點來定義路徑的數學模型。通過增加控制點的數量和位置，我們可以創建從直線到復雜曲線的各種圖形。在下一章節中，我們將深入探索Bezier曲線的數學原理，以及如何在實際應用中利用這些原理來實現更加豐富的視覺效果。

2. Bezier曲線的數學原理

2.1 Bezier曲線的定義和特性

2.1.1 Bezier曲線的幾何解釋

Bezier曲線是一種參數曲線，它通過一組稱為“控制點”的點來定義。這條曲線最顯著的特性之一是它不一定會穿過每一個控制點，而是由這些點來“引導”曲線的形狀。在幾何解釋上，可以將Bezier曲線看作是控制點定義的多邊形邊緣的“平滑化”。

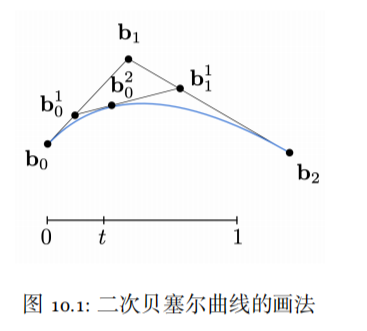
讓我們來看一個二次Bezier曲線的例子。一個二次Bezier曲線由三個控制點定義：

P0（起點）
P1（控制點）
P2（終點）

這個二次Bezier曲線可以被解釋為P0和P2之間的線段按照P1的位置進行彎曲的結果。隨著參數t從0變化到1，曲線上的點依次通過點P0、P1和P2，定義了一個平滑的過渡路徑。通過調整P1的位置，可以控制曲線的彎曲程度和方向。

2.1.2 Bezier曲線的代數形式

從代數的角度來說，Bezier曲線可以用基函數和控制點坐標來表達。對于二次Bezier曲線，其數學表達式如下：

[ B(t) = (1 - t)^2 \cdot P0 + 2 \cdot (1 - t) \cdot t \cdot P1 + t^2 \cdot P2 ]

其中，( B(t) ) 表示曲線上在參數t處的點，( P0, P1, P2 )是控制點坐標，t是參數，取值范圍在[0, 1]之間。這個公式可以用來計算曲線上任何點的位置。

在實際應用中，參數t常常被看作是時間或者迭代步長，使得我們可以沿著曲線插值計算出一系列的點，這些點可以用來繪制整個曲線的形狀。

2.2 Bezier曲線的數學基礎

2.2.1 參數方程和向量表示

Bezier曲線的參數方程使用向量形式表示，這種表示方式使得計算更為直觀和方便。例如，一個三次Bezier曲線可以用四個控制點( P_0, P_1, P_2, P_3 )和參數( t )定義如下：

[ B(t) = (1 - t)^3 \cdot P_0 + 3 \cdot (1 - t)^2 \cdot t \cdot P_1 + 3 \cdot (1 - t) \cdot t^2 \cdot P_2 + t^3 \cdot P_3 ]

其中，( t )是一個在區間[0, 1]內的參數，( B(t) )是在參數t時刻曲線上點的向量表示。

2.2.2 控制點和基函數的作用

控制點是定義Bezier曲線形狀的關鍵。每一個控制點都對曲線的形狀有影響，而這種影響的大小由基函數決定。基函數，也稱為Bernstein多項式，在Bezier曲線的方程中起到了分配參數t所代表的權重的作用。

對于二次Bezier曲線，其基函數是( (1 - t)^2, 2 \cdot (1 - t) \cdot t, t^2 )。
對于三次Bezier曲線，則是( (1 - t)^3, 3 \cdot (1 - t)^2 \cdot t, 3 \cdot (1 - t) \cdot t^2, t^3 )。

每個基函數隨著參數t的變化，在0到1之間變化，這些變化對應了在曲線形狀中不同控制點的“權重”。因此，通過調整控制點的位置，我們可以控制曲線在不同區段的彎曲程度。

2.3 Bezier曲線的構建和計算方法

2.3.1 遞歸細分算法

遞歸細分算法（也稱為De Boor-Cox算法）是一種計算Bezier曲線的常用方法。這個算法的基本思想是將一條Bezier曲線分割成兩條新的Bezier曲線，并遞歸地應用這一過程，直到曲線足夠接近直線，或者達到所需的精度。

首先，將曲線等分為兩部分，找到曲線的中點。
然后，將兩部分繼續細分，直至達到預定的分割深度。
在每次分割時，都會生成新的控制點。

這個過程可以用遞歸函數來實現，遞歸的基本步驟就是基于當前控制點計算新的控制點，然后對新控制點重復此過程。遞歸細分算法的偽代碼如下：

function DeBoorCox(controlPoints, t, depth)if depth < threshold thenreturn CalculatePoint(controlPoints, t)end if// 分割控制點newControlPoints = SplitControlPoints(controlPoints)// 遞歸計算左半部分曲線leftCurve = DeBoorCox(newControlPoints.left, t, depth - 1)// 遞歸計算右半部分曲線rightCurve = DeBoorCox(newControlPoints.right, t, depth - 1)// 合并曲線return MergeCurves(leftCurve, rightCurve)
end function

2.3.2 De Casteljau算法詳解

De Casteljau算法是另一種計算Bezier曲線的數值方法，它具有數值穩定性和幾何不變性的優點，特別適合用于計算和繪制復雜度較高的Bezier曲線。算法基于一種稱為仿射組合的概念，通過一系列的線性插值操作來計算曲線上的點。

De Casteljau算法的基本步驟如下：

在控制點上，進行線性插值以獲得新的點集。
使用新的點集重復上述線性插值過程，直到只剩下一個點。
這個最終得到的點就是參數t對應的Bezier曲線上的一點。

function DeCasteljau(controlPoints, t)points = controlPointswhile length(points) > 1 donewPoints = []for i = 0 to length(points) - 2 donewPoints.append((1 - t) * points[i] + t * points[i + 1])end forpoints = newPointsend whilereturn points[0]
end function

這個算法的一個關鍵特點是，由于它的計算過程是基于線性插值的，所以可以直觀地表示為控制點上的向量操作。De Casteljau算法的幾何解釋是，通過在控制點之間進行線性插值來逼近曲線，這為理解Bezier曲線提供了直觀的幾何理解。

3. Visual Basic中DrawBezier方法的使用

Visual Basic（簡稱VB）作為一種簡單易用的編程語言，它提供了一些用于繪制圖形和曲線的內置方法，其中?DrawBezier?方法允許用戶繪制貝塞爾曲線。本章節將深入探討如何在Visual Basic中使用?DrawBezier?方法來繪制貝塞爾曲線，包括其基礎介紹、高級應用以及優化技巧。

3.1 DrawBezier方法基礎介紹

3.1.1 方法的語法結構

DrawBezier?方法是?Graphics?類中的一個成員函數，用于繪制貝塞爾曲線。它接受四個點作為參數，分別為起點、兩個控制點以及終點。下面展示的是?DrawBezier?方法的基本語法結構：

Public Sub DrawBezier(ByVal pen As Pen, ByVal pt1 As Point, ByVal pt2 As Point, ByVal pt3 As Point, ByVal pt4 As Point)

AI寫代碼vb

pen?：定義曲線顏色、寬度和其他樣式屬性的?Pen?對象。
pt1?、?pt2?、?pt3?、?pt4?：分別是貝塞爾曲線的起點、第一個控制點、第二個控制點和終點。

3.1.2 參數詳解和實例演示

在這部分，我們將通過一個實例演示來更深入地理解?DrawBezier?方法的使用。

Private Sub Form1_Paint(sender As Object, e As PaintEventArgs) Handles Me.PaintDim g As Graphics = e.Graphics' 創建一個Pen對象，用于定義繪制的樣式Dim pen As New Pen(Color.Black, 2)' 定義貝塞爾曲線的起點、兩個控制點和終點Dim pt1 As New Point(50, 50)Dim pt2 As New Point(100, 10)Dim pt3 As New Point(200, 190)Dim pt4 As New Point(250, 250)' 調用DrawBezier方法繪制貝塞爾曲線g.DrawBezier(pen, pt1, pt2, pt3, pt4)
End Sub

在這個示例中，我們創建了一個窗體應用程序，并在窗體的?Paint?事件處理程序中使用?DrawBezier?方法繪制了一條貝塞爾曲線。通過定義四個點，我們可以看到曲線從起點開始，經過第一個控制點和第二個控制點的"拉動"，最終到達終點。

3.2 DrawBezier方法的高級應用

3.2.1 結合圖形用戶界面的應用

在圖形用戶界面中，?DrawBezier?方法可以用于繪制自定義的圖形和動畫效果。要結合GUI應用，通常需要將繪圖代碼放置在特定的事件處理程序中，例如按鈕點擊事件、定時器事件等。

在以下示例中，我們將創建一個按鈕，點擊該按鈕時，在窗體上繪制一條新的貝塞爾曲線：

Private Sub Button1_Click(sender As Object, e As EventArgs) Handles Button1.Click' 調用繪制貝塞爾曲線的過程DrawBezierCurveOnForm()
End SubPrivate Sub DrawBezierCurveOnForm()Dim g As Graphics = Me.CreateGraphics()' 創建一個藍色的Pen對象Dim pen As New Pen(Color.Blue, 3)' 定義新的貝塞爾曲線的點Dim pt1 As New Point(30, 30)Dim pt2 As New Point(150, 20)Dim pt3 As New Point(220, 200)Dim pt4 As New Point(300, 250)' 繪制貝塞爾曲線g.DrawBezier(pen, pt1, pt2, pt3, pt4)' 釋放資源g.Dispose()
End Sub

3.2.2 與其他繪圖方法的結合

為了創建更加豐富的視覺效果，?DrawBezier?方法可以與其他繪圖方法如?DrawLine?、?DrawRectangle?等結合使用。例如，可以先繪制一系列貝塞爾曲線來構建物體的輪廓，再利用其他繪圖方法填充顏色和細節。

' 繪制物體輪廓的貝塞爾曲線
g.DrawBezier(pen, pt1, pt2, pt3, pt4)' 使用FillEllipse方法填充物體的某些部分
Dim brush As New SolidBrush(Color.Green)
g.FillEllipse(brush, x, y, width, height)' 使用DrawRectangle方法繪制物體的邊緣
g.DrawRectangle(pen, x, y, width, height)

3.3 DrawBezier方法的優化技巧

3.3.1 性能優化策略

在使用?DrawBezier?方法繪制復雜圖形或大量曲線時，性能可能成為關注點。優化策略包括減少不必要的繪圖調用、緩存復雜圖形的位圖以及使用雙緩沖技術。

例如，可以使用?Graphics?對象的?DrawCachedBitmap?方法來繪制預先緩存的位圖，而不是每次都重新繪制整個圖形。

3.3.2 錯誤處理和調試技巧

在復雜的繪圖應用中，正確處理異常和進行調試是非常關鍵的。在使用?DrawBezier?方法時，必須確保所有使用的參數都是有效的，否則可能會拋出異常。

例如：

Tryg.DrawBezier(pen, pt1, pt2, pt3, pt4)
Catch ex As ExceptionMessageBox.Show("繪制失敗: " & ex.Message)
End Try

這樣可以捕獲并處理繪圖過程中可能出現的任何異常，并向用戶顯示錯誤消息。

通過上述章節內容的詳細介紹，我們了解了?DrawBezier?方法在Visual Basic中的應用，以及如何結合GUI進行高級應用，以及一些常用的優化策略。下一章節將會詳細探討貝塞爾曲線控制點的調整與平滑技術，進一步深入理解貝塞爾曲線的高級操作。

4. Bezier曲線控制點的調整與平滑技術

4.1 控制點的作用和影響

4.1.1 控制點的直觀理解

Bezier曲線通過控制點來定義曲線的形狀和路徑。這些控制點是構成Bezier曲線的幾何基礎，決定了曲線的整體形態和流線。直觀上，我們可以將控制點看作是"拉力點"，它們通過"拉扯"曲線來影響其彎曲程度和方向。當移動一個控制點時，與之相關的曲線部分就會相應地彎曲或者拉直，從而產生新的形狀。

4.1.2 如何影響曲線的形狀

控制點影響曲線的形狀遵循一定的數學規則。在二次和三次Bezier曲線中，曲線的起點和終點由首尾兩個控制點確定。中間的控制點則決定了曲線的彎曲程度和曲線的"方向"。對于二次Bezier曲線，僅有一個中間控制點；而對于三次Bezier曲線，有兩個中間控制點。

曲線平滑的關鍵在于控制點的合理布局。一個曲率變化平緩的曲線，需要控制點位置適當并且均勻分布。相反，如果需要曲線出現銳利的轉折，則需要將控制點緊密地放置在一起，或者把它們移動到離曲線較遠的位置。通過適當的控制點調整，可以實現從簡單直線到復雜曲線的各種形狀。

4.2 曲線平滑技術

4.2.1 平滑算法的原理

曲線平滑技術的核心在于調整控制點的位置，使得曲線上沒有尖銳的轉折點，整體看起來流暢自然。通常，算法會考慮以下幾個方面：

控制點間距離：減少控制點之間的距離能夠幫助平滑曲線。
控制點位置：改變控制點的位置來調整曲線彎曲的程度。
曲率連續性：確保曲線在各個控制點處曲率變化連續，無突變。

4.2.2 實現曲線平滑的具體方法

一個常用的平滑技術是使用迭代方法來微調控制點的位置。這種方法通常包括以下步驟：

對曲線上的點進行采樣，確定需要平滑的區域。
分析采樣點的曲率，識別曲率突變的點。
對于曲率突變的點，計算新的控制點位置，使得曲率變化更加平緩。
使用新的控制點重新繪制曲線，再次進行采樣與分析，重復步驟2和3，直到曲線達到預定的平滑度。

4.3 動態調整控制點實現交互效果

4.3.1 用戶輸入和控制點的關聯

在許多應用中，用戶希望實時看到控制點調整對曲線形狀的影響，這要求程序能夠動態地響應用戶的輸入，并實時更新控制點的位置。例如，用戶通過鼠標拖動控制點來調整曲線，程序需要捕捉鼠標的移動事件，并實時計算并更新控制點的新位置。這樣可以給用戶一種"所見即所得"的直觀體驗。

4.3.2 實時更新曲線的技術實現

實現曲線的實時更新，需要高效地執行以下步驟：

監聽和捕捉用戶的輸入事件（如鼠標或觸摸事件）。
根據用戶操作計算控制點的新位置。
使用新的控制點位置重新繪制Bezier曲線。
更新繪圖界面，顯示新的曲線形狀。
確保整個過程的響應速度足夠快，以實現流暢的用戶體驗。

為了實現高效更新，可以采用以下策略：

預計算和緩存?：預先計算可能會用到的值，并將它們存儲在緩存中，從而減少實時計算負擔。
分層渲染?：將曲線的繪制分解為多個層次，先繪制底層，再繪制上層，可以優化渲染效率。
雙緩沖技術?：使用兩個緩沖區，一個用于繪制，一個用于顯示，可以避免在繪制過程中產生閃爍。

下面是使用HTML5 Canvas和JavaScript來動態調整Bezier曲線控制點并實時更新的簡單示例代碼：

// HTML部分
<canvas id="myCanvas" width="400" height="400"></canvas>// JavaScript部分
const canvas = document.getElementById('myCanvas');
const ctx = canvas.getContext('2d');// 初始化控制點
let controlPoints = [{x: 50, y: 200}, {x: 150, y: 100}, {x: 250, y: 300}, {x: 350, y: 200}];// 繪制Bezier曲線的函數
function drawBezier() {ctx.beginPath();ctx.moveTo(controlPoints[0].x, controlPoints[0].y);for (let i = 1; i < controlPoints.length; i++) {ctx.bezierCurveTo(controlPoints[i].x, controlPoints[i].y,controlPoints[i].x, controlPoints[i].y,controlPoints[i].x, controlPoints[i].y);}ctx.stroke();
}// 更新控制點位置的函數
function updateControlPoints(x, y, index) {controlPoints[index] = {x: x, y: y};drawBezier();
}// 為每個控制點添加事件監聽器
for (let i = 0; i < controlPoints.length; i++) {let cp = controlPoints[i];canvas.addEventListener('mousemove', (event) => {let rect = canvas.getBoundingClientRect();let mouseX = event.clientX - rect.left;let mouseY = event.clientY - rect.top;updateControlPoints(mouseX, mouseY, i);});
}// 首次繪制曲線
drawBezier();

這段代碼首先初始化了一個Canvas，并在其中繪制了初始的Bezier曲線。每個控制點在頁面上用一個可拖動的點表示。當用戶拖動這些點時，會觸發事件監聽器，進而調用?updateControlPoints?函數更新控制點位置并重新繪制曲線。這是一個簡單的交互示例，展示了如何將用戶輸入與Bezier曲線的動態調整結合起來。

5. Bezier曲線在圖形設計、游戲開發、CAD系統等領域的應用案例

5.1 Bezier曲線在圖形設計中的應用

5.1.1 設計軟件中的曲線工具

在圖形設計中，Bezier曲線是一個不可或缺的工具。許多流行的設計軟件，如Adobe Illustrator、CorelDRAW以及Affinity Designer等，都內置了強大的Bezier曲線編輯功能。設計師通過調整控制點來精確地創建平滑的曲線和復雜圖形，Beizer曲線的應用使得圖形設計更加靈活和高效。