暑期算法訓練.2

6.力扣 11.盛水最多的容器

6.1 題目解析：

6.2 算法思路：

6.2.1 暴力解法：

6.2.2 優化算法：

6.3 代碼演示：

?編輯

6.4 總結反思：

7.力扣 611.有效的三角形個數

7.1 題目解析：

?7.2 算法思路：

7.3 代碼演示：

?編輯

?7.4 總結反思：

8.力扣 LCR.179 查找總價格為目標值的兩個商品

8.1 題目解析：

8.2 算法思路：

8.2.1 暴力解法：

8.2.2 優化解法：

?編輯8.3 代碼演示：

?編輯

?8.4 總結反思：

9.力扣 15.三數之和

9.1題目解析：

9.2 算法思路：

9.3 代碼演示：

9.3.1 正確代碼演示：

9.3.2 錯誤代碼演示：

9.4 總結反思：

10.力扣 18.四數之和

10.1 題目解析：

10.2 算法思路：

?10.3 代碼演示：

10.4 反思總結：

6.力扣 11.盛水最多的容器

6.1 題目解析：

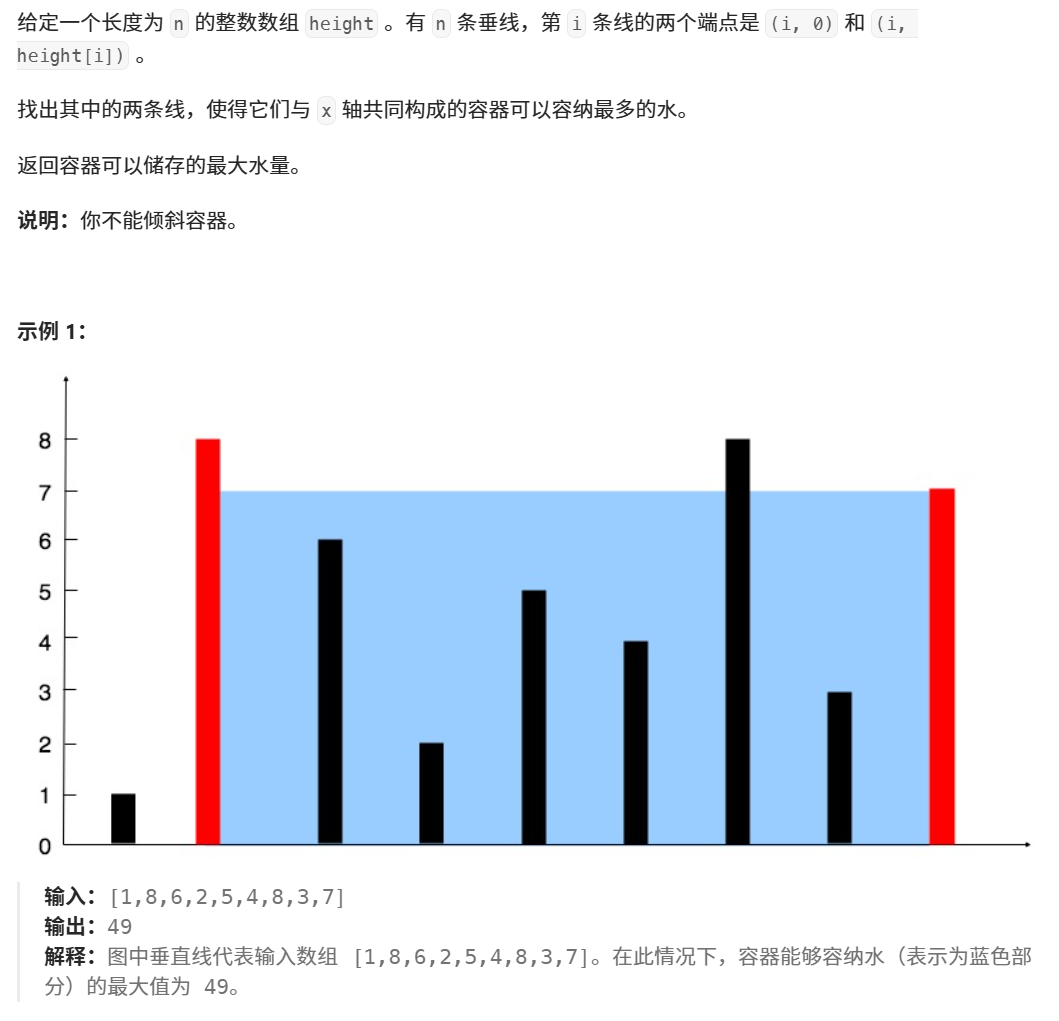
其實這道題目呢，就是讓你在給定的數組內尋找到兩個數相乘的最大值（但這i兩個數字不是隨便的兩個數，由題意可得，這個“高”其實是遵循的是短板效應，即看的是短的那一邊。）

6.2 算法思路：

6.2.1 暴力解法：

其實，當咱們看到一道題目的時候，最先想到的應該就是暴力解法，這道題也有對應的暴力解法。就是一個一個的進行枚舉，相乘，然后選出最大的值即可。當然，容器的容積的計算：

1.首先得從height[i],height[j]中選出最小的值。

2.之后計算j-i的值，之后相乘即可。

那么咱們來看一下暴力解法的偽代碼：

for(int i=0;i<n;i++)for(int j=i+1;j<n;j++)check(nums[i],nums[i])

但是這樣寫的話，一旦給的數組里面的元素特別多，就會超時，所以第一種方法不可取。

6.2.2 優化算法：

這種算法是根據暴力解法的枚舉改進而來。暴力解法為什么會超時？是因為它進行了太多的無意義的比較。?

就拿這個進行舉例子，暴力是不管三七二十一，直接全部進行相乘，然后比較。咱們其實可以帶一帶腦子，比如上圖，你讓j往左挪動，這個j-i是一直在減小的。而且，j往左挪動，由于挪動的邊始終比i小，所以高也是在不段減小的。所以這個時候，就不需要再進行比較了，因為從i到j之間，不可能有比（j-i）*j更大的。那么此時就不需要比較這一部分。

還有一點就是，咱們要移動就移動短邊，為什么呢？因為你越往內，這個長度越小，那么想找到比原來面積大的，只能靠高（找到比原來更高的高）。而咱們知道，這個受限于短板，所以高的大小得看短板，并且動短邊，高度變大的可能性更大。想一想，因為它是取決于短邊的。

所以，動的時候，先去比較左右板誰小，誰小誰就動，動完后再進行面積的計算，再比較這個面積與原面積，留下面積比較大的那一個。

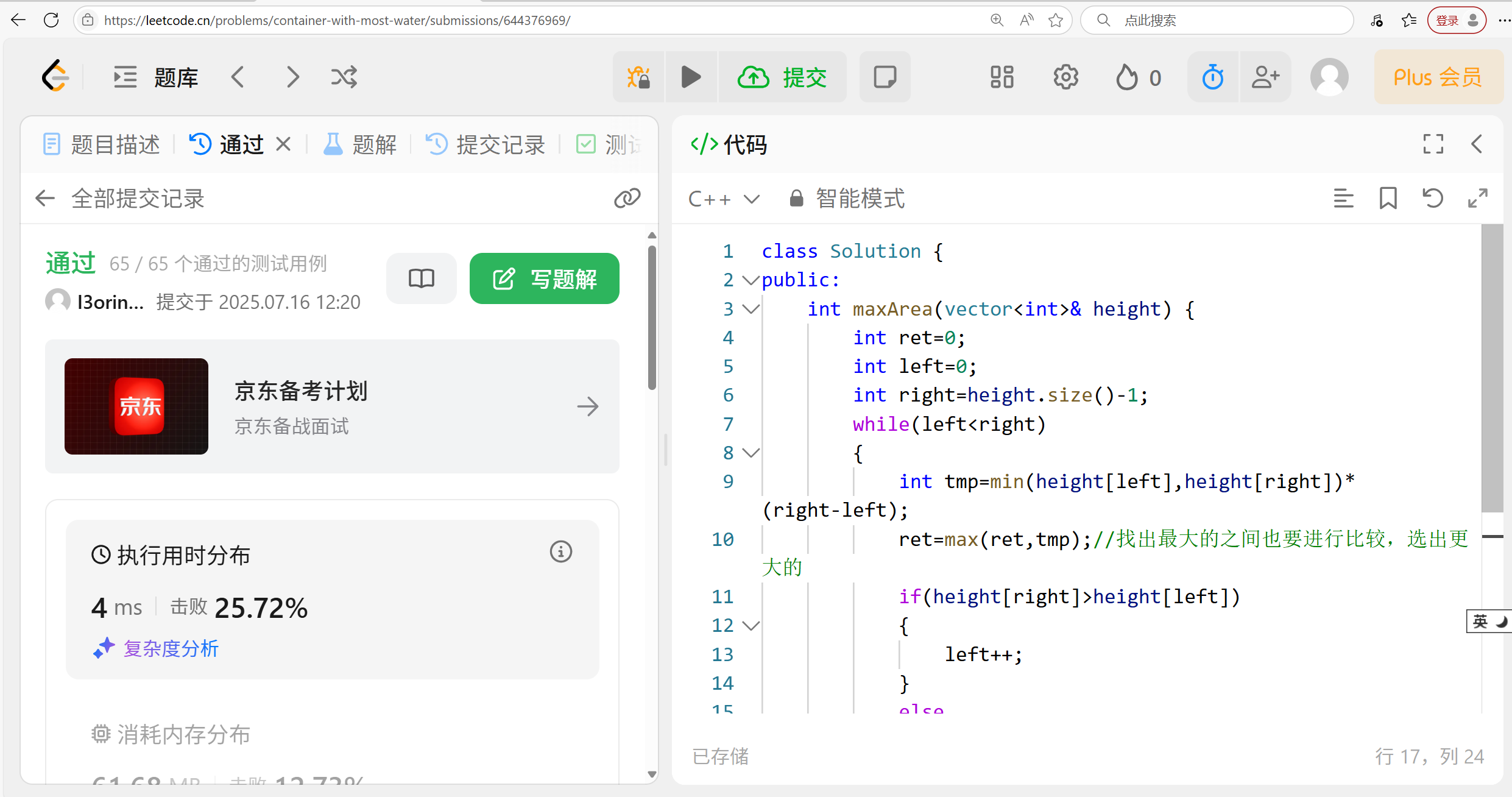
6.3 代碼演示：

int main()
{vector<int> height = { 1,8,6,2,5,4,8,3,7 };int ret = 0;int left = 0;int right = height.size() - 1;while (left < right){int tmp = min(height[left], height[right]) * (right - left);ret = max(ret, tmp);//找出最大的之間也要進行比較，選出更大的if (height[right] > height[left]){left++;}else{right--;}}cout << ret << endl;return 0;
}

?代碼就是左右板，誰小就動誰。

6.4 總結反思：

對于很多的題來說，優化的算法都是在暴力的基礎上進行改良的。所以咱們一開始想不到優化的解法，不用慌張，先寫出來暴力解法，然后再仔細的分析。

7.力扣 611.有效的三角形個數

7.1 題目解析：

這道題的題意很好理解，就是給你一個數組，返回數組里面可以組成三角形的三元組的個數即可。

?7.2 算法思路：

相信大家都知道判斷三角形的條件是任意兩邊之和大于第三邊。但是呢，這個其實需要三個條件。但是呢，還有一種方法，只需要一個條件便可以判斷出是否為三角形。

前提是咱們得知道這三條邊的大小。

好，那么接下來講解一下這道題運用到的算法思路：

找單調，然后用雙指針解決這道問題：

1.首先得先排好序，因為要用那個結論，就得保證是升序的。

2.那么利用有序數組就是使用單調性。怎么個單調法呢？

3.首先固定住一個最大的數字。

4.在最大的數字的左邊的區間內，使用雙指針法計算出符合要求的三元組的個數。

很明顯，得有兩層循環才能完成吧。

假設此時a+b>c,那么從a往右一直到b這個區間內，都是比a大的，那么這個區間內的再加上b是不是也是一定大于c的？好，那么這個時候，你要是挪動a就沒有任何意義了。這個時候，只需要往左挪動b即可。

此時的a+b<c,好，那么此時，從b往左一直到a的位置，這個區間內的值都是小于b的，所以a加上這個區間內的任意一個值，肯定也都是小于c的。所以此時挪動b無意義，需要將a往左挪動。

............以此類型。直到left>=right為止。

這才是完成了一個小循環，之后在移動c，再進行下一個小循環。

所以?

那么到現在為止，代碼相信大家都可以自己寫出來了吧。

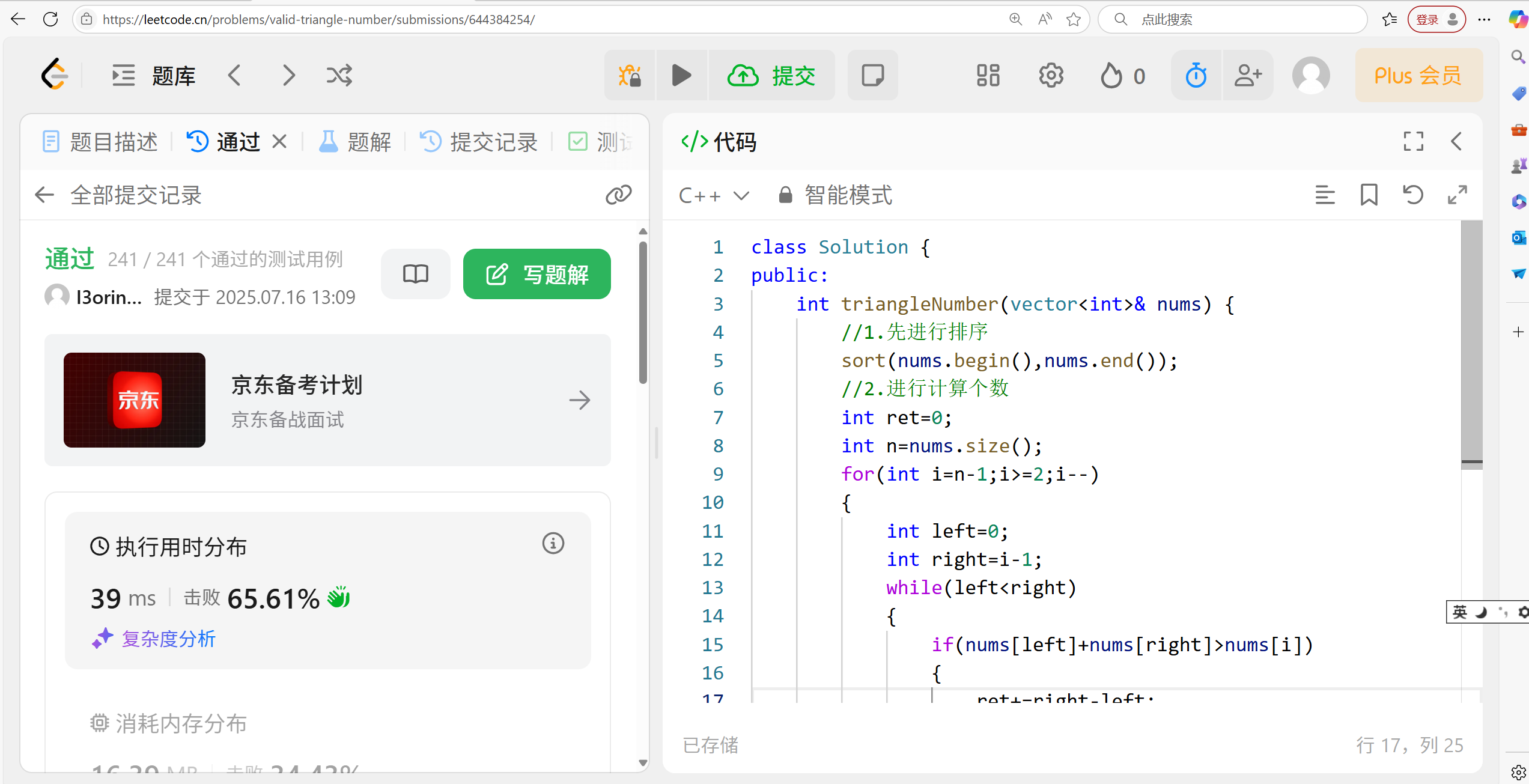
7.3 代碼演示：

int main()
{vector<int> nums = { 2,2,3,4 };//1.先進行排序sort(nums.begin(), nums.end());//2.進行計算個數int ret = 0;int n = nums.size();for (int i = n - 1; i >= 2; i--){int left = 0;int right = i - 1;while (left < right){if (nums[left] + nums[right] > nums[i]){ret += right - left;right--;}else{left++;}}}cout << ret << endl;return 0;
}

這是一個三元數組，所以c得到下標為2的位置停下。以及left與right必須得寫在for里面，因為left，right隨著c的變化為發生位置變化。?

?7.4 總結反思：

其實這道題也就是帶我們認識到了單調性+雙指針對于這類型題目的解法，為下面三道題打下了基礎。

8.力扣 LCR.179 查找總價格為目標值的兩個商品

8.1 題目解析：

題目很簡單，就是給定一個數組，再給定一個值，讓你在數組中尋找兩個元素和為目標值的二元數組，并且不管元素順序，返回一種叫即可。

8.2 算法思路：

8.2.1 暴力解法：

這道題搭眼一看，就知道肯定有暴力解法，就是寫兩層for循環，然后再將元素想加，看看哪兩個元素相加等于目標值，再返回這兩個元素組成的二元數組。但是這種解法容易超時，所以咱們重點來講解第二種優化算法。

8.2.2 優化解法：

其實這個題的解法與上一題的解法基本一致，咱們來看圖理解：

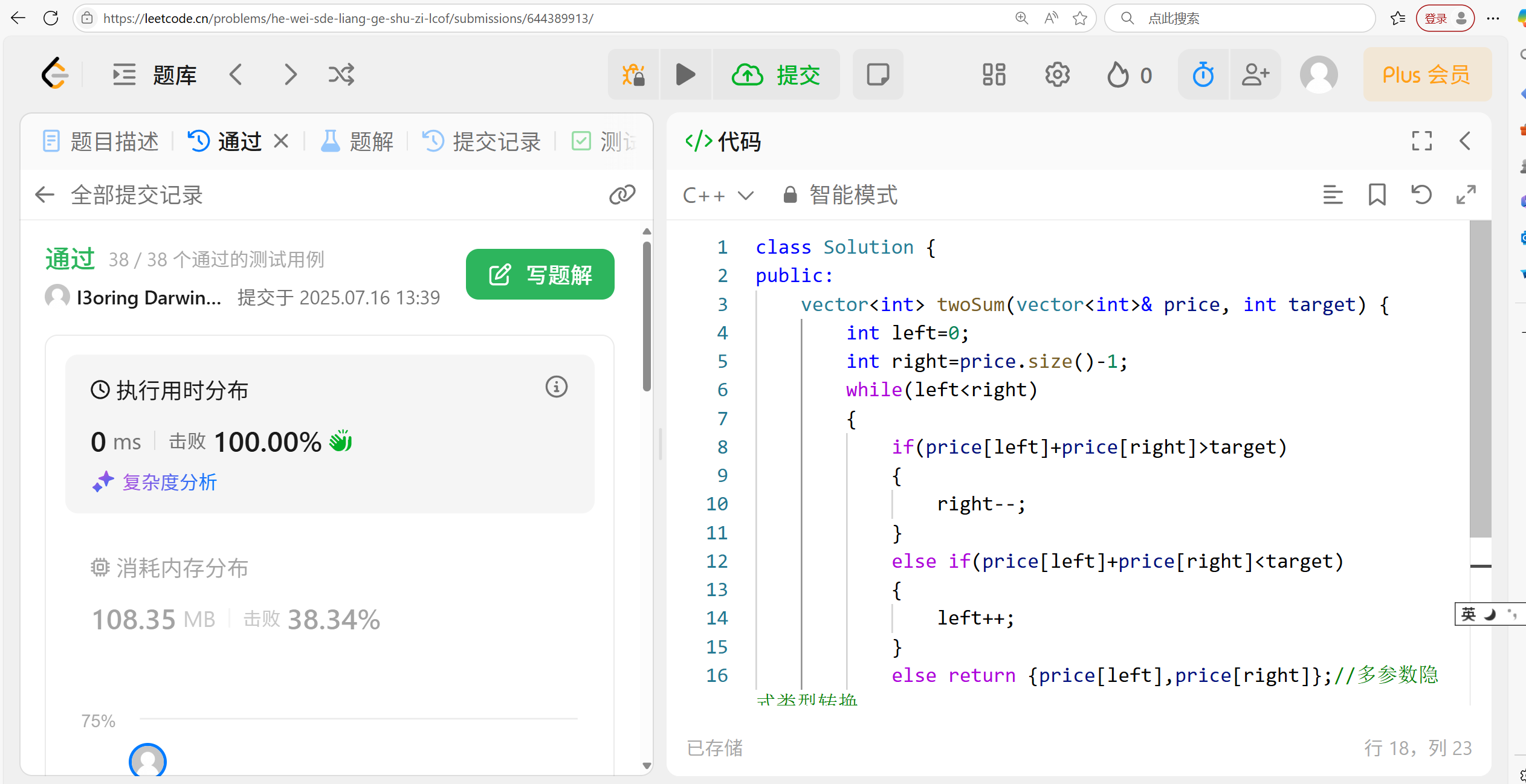
8.3 代碼演示：

vector<int> Judgment(vector<int>& price, int target)
{int left = 0;int right = price.size() - 1;while (left < right){if (price[left] + price[right] > target){right--;}else if (price[left] + price[right] < target){left++;}else return { price[left],price[right] };//多參數隱式類型轉換}return{ -1,-1 };//確保每個路徑下都有返回值
}

?8.4 總結反思：

這道題與上一道題的解法基本一致。

9.力扣 15.三數之和

9.1題目解析：

題目也挺好理解的，就是i，j，k三個元素相加為0，并且這三個元素不可以是同一個位置的，并且返回的時候，三元數組中的元素相同的，只能返回一組，這個意味著咱們是不是要進行去重呀。那去重的話，咱們肯定可以想到C++里面的unordered_set，使用容器去重。當然可以，但是，有沒有不使用容器就可以進行去重的呢？有！方法，咱們算法思路里面講解。

9.2 算法思路：

其實，這道題，你只要做過前面的那個題，這個題的算法思路就很容易想到。

好，這個題基本的核心的思路我已經全部羅列出來了，大家可以看一下。但這個地方，本博主寫代碼的時候，還是被弄暈了。

9.3 代碼演示：

9.3.1 正確代碼演示：

vector<vector<int>> threeSum(vector<int>& nums)
{sort(nums.begin(), nums.end());vector<vector<int>> ret;int n = nums.size();int i = 0;while (i < n){int left = i + 1; int right = n - 1;while (left < right){if (nums[left] + nums[right] == -nums[i]){vector<int> frontret = { nums[left],nums[right],nums[i] };ret.push_back(frontret);left++, right--;// 去重操作left和right，先++left,--right,再去重//先去重，再移動left與right的方法不可取while (left < right && nums[left] == nums[left - 1]) left++;while (left < right && nums[right] == nums[right + 1])right--;}else if (nums[left] + nums[right] > -nums[i]){right--;}else {left++;}}i++;//外層i去重while (i < n && nums[i] == nums[i - 1]) i++;}return ret;
}
int main()
{vector<int> nums = { 2,-3,0,-2,-5,-5,-4,1,2,-2,2,0,2,-4,5,5,-10 };vector<vector<int>> kk = threeSum(nums);for (auto& e : kk){for (auto& m : e){cout << m << "";}cout << endl;}cout << endl;
}

這個地方的去重操作呢，必須得是先進行left，right的移動，之后再判斷這個位置與前一個位置的數字是否相等，如果相等，再加加，挪到要改變的那個元素的位置上。這是正確的邏輯。但是博主呢，正好邏輯相反，結果就這一個題在那里調試了一下午。

9.3.2 錯誤代碼演示：

去重邏輯混亂，不可取
vector<vector<int>> threeSum(vector<int>& nums)
{sort(nums.begin(), nums.end());vector<vector<int>> ret;int n = nums.size();int i = 0;while (i < n){int cout_i = 0;int left = i + 1; int right = n - 1;while (left < right){int cout_left = 0;int cout_right = 0;if (nums[left] + nums[right] == -nums[i]){vector<int> frontret = { nums[left],nums[right],nums[i] };ret.push_back(frontret);while ((left + 1 < n - 1) && (nums[left] == nums[left + 1])){if (left < n - 1){left += 1;cout_left++;}}while ((right - 1 > i + 1) && (nums[right] == nums[right - 1])){if (right > i + 1){right -= 1;cout_right++;}}if ((left < n - 2) && (cout_left == 0)){left++;}if ((right > i + 2) && (cout_right == 0)){right--;}}else if (nums[left] + nums[right] > -nums[i]){right--;}else {left++;}}while ((i + 1 < n - 2) && (nums[i] == nums[i + 1])  ){if (i < n - 2){i += 2;cout_i++;}}if (cout_i == 0){i++;}}return ret;
}
int main()
{vector<int> nums = { 2,-3,0,-2,-5,-5,-4,1,2,-2,2,0,2,-4,5,5,-10 };vector<vector<int>> kk = threeSum(nums);for (auto& e : kk){for (auto& m : e){cout << m << "";}cout << endl;}cout << endl;
}

這是我寫的代碼，我的本意是想著既然都去重了，那就先去重，如果重復了，那就加到不重復為止，且這種最后不需要再單獨加加了。之后再單獨加。但是呢，不對?。

1. **去重指針移動不正確**：在找到一組解后，對`left`和`right`的去重沒有正確地將指針移動到下一個不同元素的位置。例如，如果`left`位置有重復，它只是移動到了重復序列的最后一個，然后停止，這樣下一次循環還是相同的值（因為下一次循環時，`left`指向的還是重復序列的最后一個，而下一個元素就是不同的，但此時`left`并沒有指向下一個不同元素，所以循環會繼續使用這個重復序列的最后一個元素，導致重復解）。

2. **去重后指針移動邏輯混亂**：通過`cout_left`和`cout_right`來決定是否再移動一次，這種邏輯沒有道理。而且，在去重循環中，它只移動了重復元素，但并沒有確保移動后的指針指向的是一個新的值（即跳過重復后應該指向下一個不同的值）。

3. **固定數`i`的去重邏輯錯誤**：使用`i+=2`來跳過重復，這會導致當重復次數為奇數時，最后一個重復值仍然會被處理，造成重復解。而且，當重復次數超過2次時，跳躍步長固定為2，顯然不夠。

只能說，我還是個新手吧哈哈哈哈，做題做的還是少。

9.4 總結反思：

這道題想要真正的自己用代碼實現出來，真的挺不容易的。還是要多練習題目。

10.力扣 18.四數之和

10.1 題目解析：

你仔細的讀一讀這道題，會發現，這道題的解法與前面那個三數之和的解法基本一致。無非就是外面多套了層循環，多加了一個去重。

10.2 算法思路：

若還是不能夠理解，那么我畫一張圖就可以了：

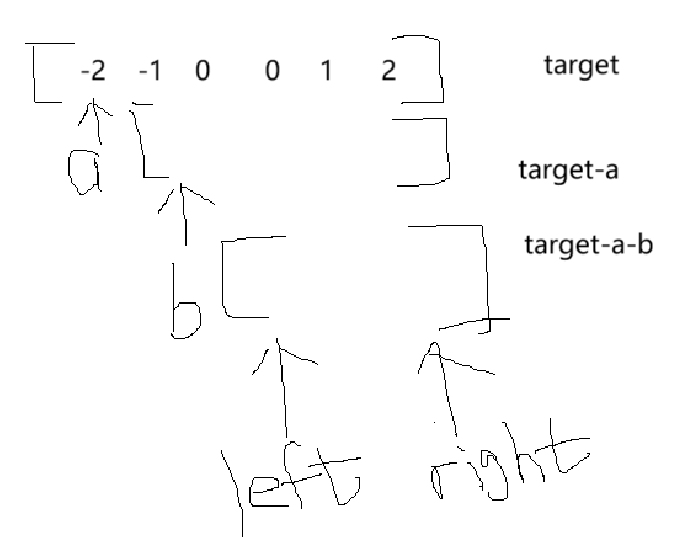1.依次固定一個數a

2.在a后面的區間內，利用“三數之和”找到三個數，使這三個數的和等于target-a即可

? ? ? ? 2.1 依次固定一個數b

? ? ? ? 2.2 在b后面的區間內，利用“雙指針”找到兩個數，使得兩個數的和為target-a-b即可

最后別忘了去重細節，有三個，left與right，b，a

以及還有越界的情況。最后考慮清楚，會發現與三數之和的代碼差不多一樣的。?

?10.3 代碼演示：

//四數之和思想與三數之和基本一致，連去重方法都是一樣的
vector<vector<int>> fourSum(vector<int>& nums, int target) {vector<vector<int>> ret;sort(nums.begin(), nums.end());int n = nums.size();for (int i = 0; i < n;) {for (int j = i + 1; j < n;) {int left = j + 1;int right = n - 1;long long aim = (long long)target - nums[i] - nums[j];while (left < right) {if (nums[left] + nums[right] ==aim) {vector<int> frontret = { nums[left], nums[right],nums[i], nums[j] };ret.push_back(frontret);++left;--right;// 只有這樣寫才能確保最后一個位置的元素是在不重復的那個位置底下while (left < right && nums[left] == nums[left - 1]) {left++;}while (left < right && nums[right] == nums[right + 1]) {right--;}}else if (nums[left] + nums[right] >aim) {right--;}else {left++;}}j++;while (j < n && nums[j] == nums[j - 1]) {j++;}}i++;while (i < n && nums[i] == nums[i - 1]) {i++;}}return ret;
}

?三個去重以及邊界判定別忘了。