線性代數

?外積與矩陣乘法的等價性

歐拉角的奇異性--萬向死鎖

現象

第二個軸旋轉度，會導致第三個旋轉軸和惡原始坐標軸的第一個旋轉軸重合，導致第一次旋轉與第三次旋轉都使用了同一個軸進行旋轉，也就是本質上旋轉三次，但是只在兩個自由度上旋轉。

eg:

如下圖，第二次的繞Y轉90度之后，X就變到了初始坐標系下的Z軸方向上，第三次的繞X軸旋轉，本質上還是繞空間中的這個坐標系的初始坐標的Z軸的自由度旋轉。丟失了一個自由度。

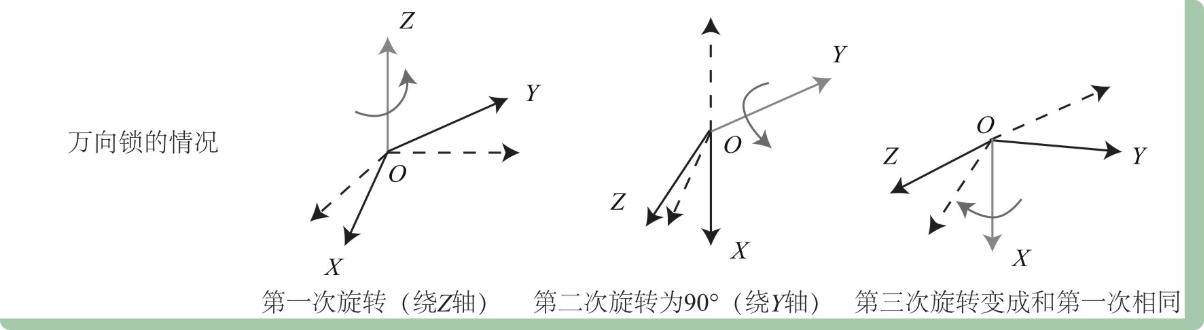
丟失一個自由度會導致什么問題

(1)旋轉耦合

自由度丟失，導致第三次旋轉的效果丟失，在最終的旋轉矩陣中沒有表現出來，也導致旋轉矩陣中第一次旋轉和第二次旋轉的旋轉角耦合，無法分離出角度。

(2) 控制指令沖突

• 如果系統試圖調整航向（ψ），實際會影響橫滾（?），反之亦然。

• 示例（無人機）：

  • 飛控發送“增加航向角”指令，但實際可能同時改變橫滾角，導致機體失控

解決方案

(1) 使用四元數（Quaternion）

• 優勢：四元數通過4D空間描述旋轉，無奇異性問題，適合連續旋轉和插值（如球面線性插值SLERP）。

• 轉換方法：歐拉角可轉換為四元數處理，但需注意歸一化和插值路徑。