數組(Array)
數組是最基礎的數據結構,在內存中連續存儲,支持隨機訪問。適用于需要頻繁按索引訪問元素的場景。
簡介
數組是一種線性結構,將相同類型的元素存儲在連續的內存空間中。每個元素通過其索引值(數組下標 index)來進行唯一標識和訪問。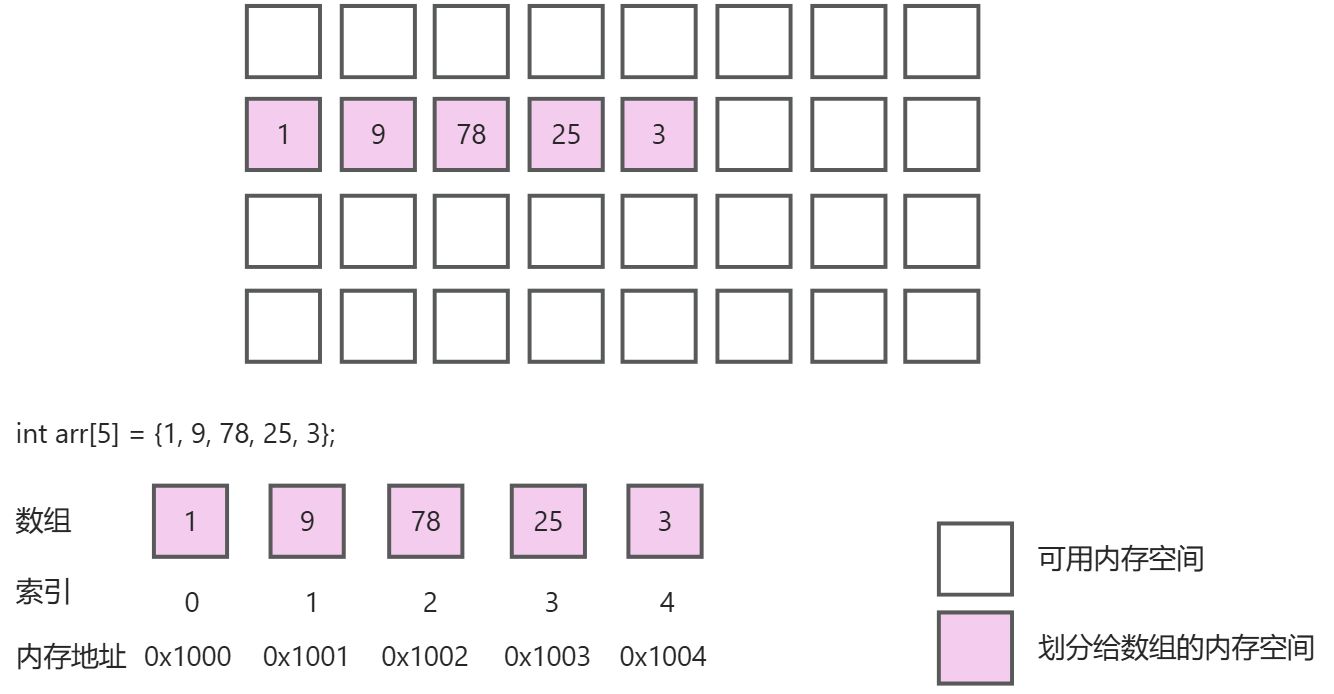
核心特性
- 固定大小:在絕大多數語言中,數組創建后大小固定不變
- 連續內存:元素在內存中順序存儲,無額外開銷
- 隨機訪問:O(1)時間復雜度直接訪問任意元素
- 同質性:同意數組中所有元素類型相同
- 索引訪問:通過數字索引訪問元素
基本操作
時間復雜度分析
| 操作 | 時間復雜度 |
|---|---|
| 訪問 | O(1) |
| 更新 | O(1) |
| 遍歷 | O(n) |
| 搜索 | 無序數組O(n);有序數組O(log n)(二分查找) |
| 插入/刪除 | 在末尾O(1);在數組指定位置O(n)(需要移動元素) |
代碼實現
// 聲明和初始化
int[] numbers = new int[5]; // 創建一個長度為5的int數組,默認值都是0
int[] primes = {1, 9, 78, 25, 3}; // 直接使用初始值創建數組// 訪問元素
int firstPrime = primes[0]; // 得到1// 更新元素
numbers[0] = 10;// 獲取數組長度
int length = numbers.length;// 遍歷數組
for (int i = 0; i < primes.length; i++) {System.out.println(primes[i]);
}// 使用增強for循環遍歷
for (int prime : primes) {System.out.println(prime);
}/* 隨機訪問元素 */
int randomAccess(int[] nums) {// 在區間 [0, nums.length) 中隨機抽取一個數字int randomIndex = ThreadLocalRandom.current().nextInt(0, nums.length);// 獲取并返回隨機元素int randomNum = nums[randomIndex];return randomNum;
}優缺點
優點
- 空間效率高:數組為數據分配了連續的內存塊,無需額外的結構開銷
- 支持隨機訪問:數組允許在 O(1) 時間內訪問任意元素
- 緩存局部性:當訪問數組元素時,計算機不僅會加載該數組,還會緩存其周圍的其他數據,從而借助高速緩存來提升后續操作的執行速度
缺點
- 插入與刪除效率低:當數組中的元素較多時,插入/刪除元素都得移動大量的元素
- 長度不可變:數組在初始化后長度就固定了,擴容數組需要將原數組所有數據復制到新數組,開銷很大
- 空間浪費:如果數組空間分配大小超過了實際所需,多余空間容易浪費
應用場景
- 隨機訪問:如果需要隨機抽取一些樣本,可以用數組存儲,并生成一個隨機序列,根據索引實現隨機抽樣
- 排序和搜索:數組是排序和搜索算法中常用的數據結構。快速排序、歸并排序、二分查找等都主要在數組上進行
- 查找表:當需要快速查找一個元素或其對應關系時,可以使用數組作為查找表。如實現字符到 ascii 碼的映射,可以將字符的 ascii 值作為索引,對應元素存放在數組中對應位置
- 機器學習:神經網絡中使用了大量的向量、矩陣、張量之間的線性代數運算,這些數據都是以數組的形式構建的。數組是神經網絡編程中最常用的數據結構
- 數據結構實現:數組可以用于實現棧、隊列、哈希表、堆、圖等數據結構
擴展
- 二維數組
- 多維數組
熱門題目
- 53. 最大子數組和
- 11. 盛最多水的容器
- 283. 移動零
- 88. 合并兩個有序數組
53. 最大子數組和
給你一個整數數組 nums ,請你找出一個具有最大和的連續子數組(子數組最少包含一個元素),返回其最大和。子數組是數組中的一個連續部分。
示例:
輸入:nums = [-2,1,-3,4,-1,2,1,-5,4]
輸出:6
解釋:連續子數組 [4,-1,2,1] 的和最大,為 6 。
題解:
動態規劃
分而治之,避免重復計算
- 初始化
maxSum設置為數組第一個元素currentSum也設置為第一個元素(子數組最少包含一個元素)
- 遍歷數組
- 從第二個元素開始遍歷
- 對于每個元素
nums[i],有兩種選擇:- 將其加入到之前的子數組,即
currentSum + nums[i] - 重新開始一個子數組,只包含當前元素,即
nums[i]
- 將其加入到之前的子數組,即
- 選擇最大的作為新的
currentSum - 最后,更新
maxSum,保證其是currentSum和maxSum中最大的值
class Solution {public int maxSubArray(int[] nums) {int maxSum = nums[0];int currentSum = nums[0];for(int i = 1; i < nums.length; i++) {// 是將當前元素加入到之前的子數組,還是重新開始一個子數組currentSum = Math.max(currentSum + nums[i], nums[i]);// 更新最大子數組和maxSum = Math.max(currentSum, maxSum);}return maxSum;}
}

參考資料
[1] Hello 算法
[2] 算法導航






)











)
