AOE網：

用E=Edge表示活動，AOV網是用Vertex頂點表示活動

僅有一個入度=0的頂點叫開始頂點(源點)，出度=0的頂點叫結束頂點(匯點)

各條邊表示活動，邊上的權值表示完成該活動的開銷，各頂點表示事件，事件是就發生在某個時刻，活動是持續一段時間的

1.只有事件發生后才可進行活動，如下只有開始事件發生后才可打雞蛋或者洗番茄

2.只有指向該頂點事件的各邊所代表的活動都完成了指向的事件才可發生，如打雞蛋和切番茄活動都完成后才可發生可以炒了事件

3.從一個頂點往外指出多條邊，意味著這些邊上的活動可以并行進行，比如開始事件發生后，打雞蛋和切番茄可以并行執行

關鍵路徑：

從源點到匯點有多條路徑，路徑長度(經過的邊上的權值之和)最大的一條叫關鍵路徑，關鍵路徑上的活動稱為關鍵活動，關鍵路徑意味著要完成某個事兒至少需要關鍵路徑長度時間，關鍵活動意思是要完成某個事兒這些活動都不能少

如下圖有：開始->可以切了->可以炒了->結束、開始->打雞蛋->可以炒了->結束兩條路徑，前一條路徑長度:1+3+2=6,后一條路徑長度：2+2=4，即前一條為關鍵路徑

活動余量=最遲開始時間-最早開始時間，活動余量=0的活動表示是關鍵活動，即不能拖延的活動

匯點的最遲發生時間=匯點的最早發生時間

求關鍵路徑步驟：

各個事件發生的最早開始時間=對應各個活動的最早開始時間，從開始頂點推算出各頂點最早開始時間，通過結束頂點逆推出各個頂點的允許的最遲發生時間，進而得出各個活動的最遲發生時間

求所有事件的最早發生時間：

還得求拓撲序列，再按照拓撲序列去求各個頂點的最早發生時間

求所有事件的最遲發生時間(取最小的)：

還得求逆拓撲序列，再按照逆拓撲序列去求各個頂點的最遲發生時間

?

求所有活動的最早發生時間：

活動發生的最早時間=活動的弧尾連接的頂點的最早發生時間，如下圖中的a4活動最早時間為弧尾連接的V2的最早發生時間

?

求所有活動的最遲發生時間：

?活動發生的最遲時間=活動指向頂點的最晚發生時間-活動所在邊的權值

求所有活動的時間余量：

?活動的時間余量=活動的最晚發生時間-活動的最早發生時間

找到時間余量=0的活動，這些活動所在的邊連接起來的路徑就是關鍵路徑

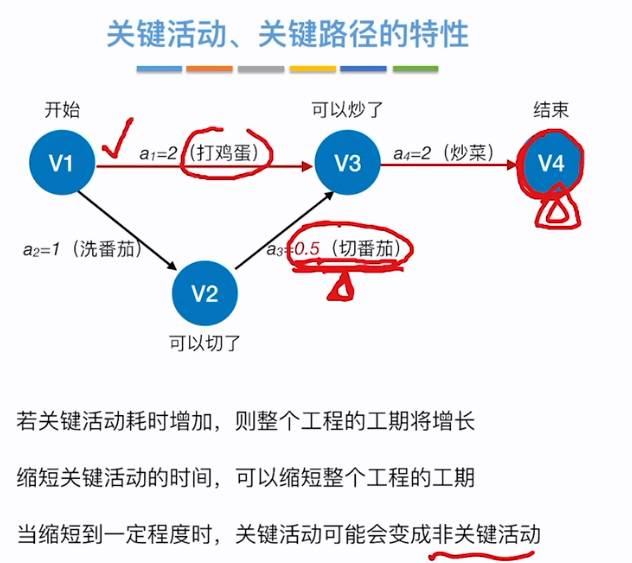
關鍵活動、 關鍵路徑的特性：

當關鍵活動的時間被縮短到一定時間時可能會變成非關鍵活動，此時關鍵路徑也會發生變化，如下切番茄由關鍵活動壓縮時間到0.5，此時洗番茄+打雞蛋+炒菜=1+0.5+2=3.5<打雞蛋+炒菜=2+2=4，此時關鍵路徑已經發生改變，因為切番茄已經不是關鍵活動，所以繼續縮短切番茄的時間也不會影響最后的結束時間了?

在一個aoe網中可能有多條關鍵路徑：

多條關鍵路徑下，只縮短一條關鍵路徑上的關鍵活動的時間并不能縮短整個工期，只有把所有關鍵路徑上的某些或全部關鍵活動時間都縮短或者把把某個在所有關鍵路徑上的關鍵活動的時間縮短才能縮短整個工期

知識回顧：

?

水一篇文字。。。。。。。。。。。

?