1. 紅黑樹：

紅黑樹從根節點開始的最長的路徑不會超過最短路徑的2倍。

紅黑樹的話，他的結點的分布沒有我們的AVL樹的結點的分布均衡，但是效率也不錯，AVL樹的結點分布的那么均勻，其實也是在進行了旋轉，付出了代價換來的絕對的均衡。

那么紅黑樹的“紅黑樹從根節點開始的最長的路徑不會超過最短路徑的2倍”是怎么被維持的呢？

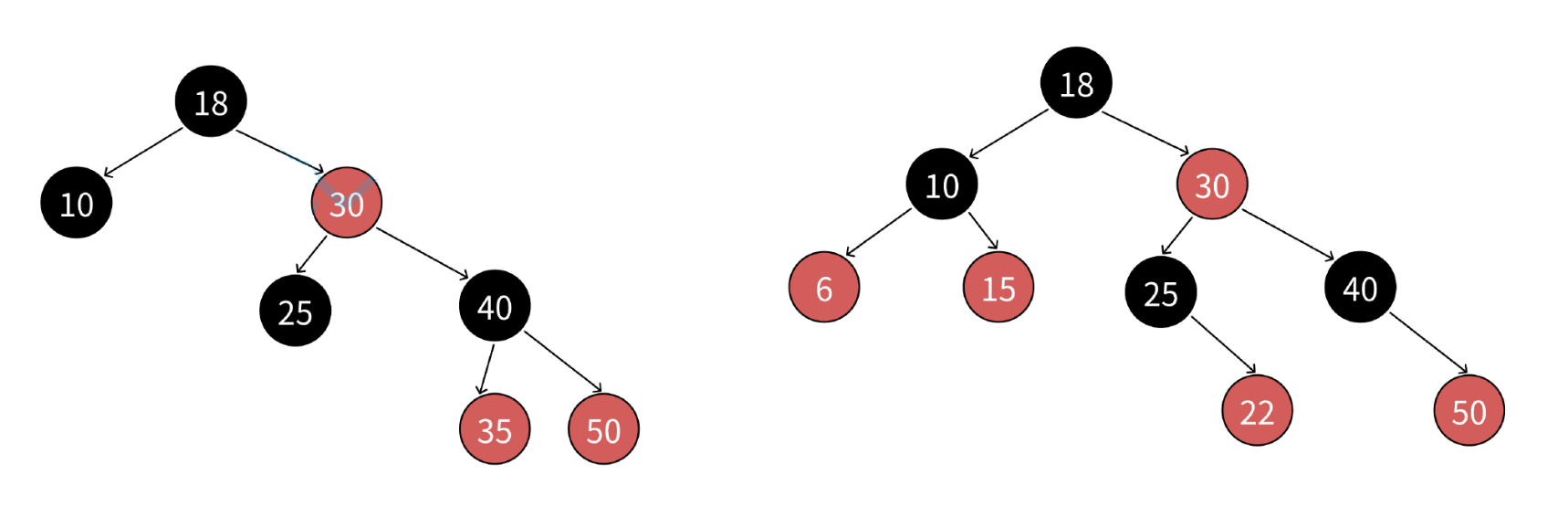
這兩個是我們的紅黑樹，第一個紅黑樹的左邊全黑的路徑就是最短路徑，右邊一黑一紅的是最長的路徑，最長路徑<=最短路徑的2倍；

那我們來數一下我們的這兩個紅黑樹的路徑有多少跳呢？

我們的第一個紅黑樹的路徑有8條，第二個有10條。（我們數路徑一定要數到空結點，我們的第一個二叉樹的10結點下面還有兩個空的結點）

這個二叉樹不是我們的紅黑樹，他的最短的路徑是最左邊的，只有一個黑節點，但是我們的右邊的最長的路徑有兩個黑節點，這就不符合我們的紅黑樹的規則。

最短和最長路徑：

在我們的紅黑樹里面，全黑的那條路徑就是最短的路徑，一紅一黑的路徑是最長的路徑；

紅黑樹沒有AVL樹那樣的絕對的平衡，但是效率也不錯，紅黑樹的旋轉次數更少；

2. 紅黑樹的插入：

我們給紅黑樹里面插入新節點的時候，我們可以是插入黑色結點，也可以是插入紅色結點，但是如果插入黑色結點的話，這個黑色結點影響了這條路徑的黑色結點的數量，我們的每條路徑的黑色結點的數量可能都會發生變化來保持他們每條路徑的黑色結點的數量的相等，這個是很難控制的。

所以我們必須要插入紅色結點，當然，如果這個樹連根都沒有的話，根節點要求是黑結點，我們就插入一個黑結點。

uncle結點的情況的劃分：

插入紅結點，我們的叔叔結點分為三種情況，我們先看第三種情況：uncle結點存在且為紅：

uncle結點存在且為紅：

看這個圖片，當我們給parent結點的下面插入一個紅結點的時候，這時候我們的parent結點和cur結點都是我們的紅色的結點，（因為我們的紅黑樹的規則說明，我們是不能有兩個紅色結點同時在的）。

常規的處理辦法：（變色）

這時候我們看我們的uncle結點，uncle結點是紅色結點，這時候我們就把parent結點和uncle結點都變成黑色結點，然后把grandparent結點變成紅色結點。（這個就是我們一般變色的方法）。

這時候我們看我們的圈出來的部分就變正常了，然后每條路徑的黑色結點的數量也是一樣的。但是出現了新的問題，那就是我們的紅黑樹又出現了兩個紅色結點連接的情況。

這時候我們就再來一次我們剛才的操作，我們把之前的grandparent結點看成我們的新的cur結點，然后找到新的parent，uncle，grandparent結點。

這時候我們重復剛才的操作，我們看我們的uncle結點，這個時候的話，我們的uncle結點就來到了我們的第二種情況，那就是我們的uncle結點存在且為黑色節點。

我們的第二種的uncle結點存在且為黑色結點的這種情況的話，他只會出現在我們的下面的子樹的根節點由黑色變成紅色上來的，不然的話，直接插入紅色結點的話，uncle結點是不可能為黑色的，不然不符合紅黑樹的規定。

就好比這種情況，我們給插入一個紅色結點后，紅色結點cur的叔叔結點uncle直接就是黑色結點，這種情況要是有的話，說明這個紅黑樹還沒有插入結點的時候，這就是一個錯誤的紅黑樹。

這種情況只會是我們變了一層以后，繼續的往上面去找，然后再往上層的uncle可能會有的情況；

我們往回來看：

uncle結點存在且為黑：

我們現在的叔叔uncle結點現在是黑色結點，這時候我們的剛才的常規的處理的方法就不行了，但是我們還是要想辦法來處理他，因為他的最長了路徑已經超過了我們的最短路徑的長度了。

這時候我們的剛才的常規的變色的處理方法已經不夠用了，我們這時候就要使用旋轉來解決了。

旋轉的話，我們分為單旋和雙旋，我們看情況使用這兩個旋轉方式。

旋轉：

//這個是我們的單旋：

我們看這個，這時候我們的uncle結點為黑色結點，我們的兩個紅色結點相連接，左邊的結點比較冗余，我們就進行一個右單旋，parent結點作為我們的根節點，然后grandparent結點變成紅色結點作為我們的parent結點的右孩子結點。

//核心是旋轉完后我們把parent結點的顏色變成黑色，然后把grandparent結點的顏色變成紅色。

下面的是我們的雙旋：

旋轉的話，我們已經比較熟悉了，我們看上面的，我們要把cur結點作為我們的最上面的結點，我們把cur的左孩子作為parent的右孩子，然后把cur的右孩子變成grandparent的左孩子。

旋轉結束以后，我們的cur結點就變成了我們的這顆樹的根，這個節點有可能是我們的整棵樹的根節點，也有可能只是一個子樹的根，但是不管怎樣，我們都把cur結點的colour置為BLACK。

然后把grandparent的colour置為RED。????????

uncle結點不存在：

當我們的uncle結點不存在的話，我們的cur結點一定是新增的，不可能是由下面的黑結點演變過來的，因為當我們的uncle結點不存在的時候，我們的parent這邊的話，他是不能有黑色結點的，所以不可能是演變來的。

這種情況的話，我們是一定要想辦法處理掉的，因為后面的路徑有兩個紅結點是相連的，并且的這條路徑已經超過了我們的最短路徑的長度。?

這時候我們的變色就解決不了這個問題了，我們就要使用旋轉來解決；

這個是我們的單旋：

比如上面的這個，我們就使用一個右單旋就可以解決，然后把我們的parent結點變成黑色結點，然后grandparent結點變成紅色結點，parent有可能是整顆紅黑樹的根，也有可能只是一顆普通紅黑樹的子樹的根，但是最后我們都要把它置為黑節點。

下面的是我們的雙旋：

這個紅黑樹沒有uncle結點，然后他是左邊高的右邊高，我們就要使用一個雙旋來解決，使用一個左右雙旋來解決。（我們之前學習的雙旋，我們可以靈巧的記憶一下，我們的cur結點要做到我們的最高的結點，然后cur結點的左孩子給parent的右孩子，cur結點的右孩子做成我們的grandparent的左孩子）。

總結：

這個是我們的uncle結點為紅結點，并且parent和uncle結點變成黑節點，grandparent結點變紅結點之后就可以處理掉的情況。

這個是我們的uncle結點是空結點的情況，我們需要使用旋轉來處理。

這個是我們的uncle結點先是紅結點，parent和uncle結點變黑，grandparent結點變紅之后，但是我們的紅黑樹還是有問題的，這時候我們的常規的（parent，uncle，grandparent）變色已經解決不了了，我們就得旋轉來解決了。

我們總結一下：我們的上面的三個圖片就是對應了我們的uncle結點的三種情況；

紅黑樹的插入的代碼的實現：