一、原理——合作博弈論
SHAP（SHapley Additive exPlanations）是一種用于解釋機器學習模型預測結果的方法，它基于合作博弈論中的 Shapley 值概念。Shapley 值最初用于解決合作博弈中的利益分配問題。假設有 n 個參與者共同合作完成一項任務并獲得一定收益，Shapley 值能公平地分配這個總收益給每個參與者，它考慮了每個參與者在所有可能的合作組合中的邊際貢獻。
在機器學習中，特征的邊際貢獻指的是某個特征在模型中對預測結果所帶來的額外價值或影響。它衡量了在已有其他特征的基礎上，單獨添加該特征后模型性能的提升程度。
例如：甲、乙、丙、丁四個工人一起打工，甲和乙完成了價值100元的工件，甲、乙、丙完成了價值120元的工件，乙、丙、丁完成了價值150元的工件，甲、丁完成了價值90元的工件，那么該如何公平、合理地分配這四個人的工錢呢？
這里每個工人獲得的工錢反映了他在不同組合中對最終價值產出的獨特貢獻。這里通過對比不同工人組合完成工件價值的差異，來確定每個工人的貢獻。比如從 “甲和乙完成價值 100 元工件” 到 “甲、乙、丙完成價值 120 元工件”，差值 20 元體現了丙在這個組合變化中的貢獻，即丙的工錢。
二、shapley值計算思路
特征組合枚舉：對于一個有 n 個特征的模型，需要考慮所有可能的特征子集組合。例如，當有 3 個特征 A、B、C 時，特征子集包括空集 {}，單特征集 {A}、{B}、{C}，雙特征集 {A, B}、{A, C}、{B, C}，以及包含所有特征的集合 {A, B, C}。總共有 ?種組合。
邊際貢獻計算：對于每個特征子集 S ，計算包含該特征 i （ i ??S ）和不包含該特征 i （即子集 S ）時模型預測值的差異，這個差異就是特征 i 在特征子集 S 下的邊際貢獻。
平均邊際貢獻（shap值）：對特征 i 在所有可能的特征子集組合下的邊際貢獻進行加權平均，權重是該子集組合出現的概率，得到的結果就是該特征的 SHAP 值。正值表示該特征傾向于使模型預測值增加，負值表示傾向于使模型預測值減少。
三、shap的關鍵特性
基準值代表了在沒有考慮任何特定樣本特征時，模型基于整個訓練數據集的平均預測輸出。例如，在一個預測房價的模型中，如果對訓練數據集中所有房屋的價格求平均，得到的這個平均價格就是基準值。它為解釋模型對特定樣本的預測提供了一個參考點。
加性特性解釋：SHAP 的加性特性表明，對于任何一個樣本的預測，模型預測值可以分解為基準值與每個特征的 SHAP 值之和。也就是說，每個特征對模型預測值的貢獻是獨立可加的。
假設有一個預測客戶是否會購買產品（0 ：不購買，1 ：購買）的模型，基準值為 0.3（即平均來看，在不考慮任何客戶特征時，模型預測客戶購買產品的概率是 0.3）。對于某個特定客戶，特征 1（比如客戶年齡）的 SHAP 值為 0.1，特征 2（比如客戶收入）的 SHAP 值為 0.2，特征 3（比如客戶購買歷史）的 SHAP 值為 0.05。根據 SHAP 的加性特性，該客戶的模型預測值就是基準值加上各個特征的 SHAP 值，即 0.3+0.1+0.2+0.05=0.65 ，這意味著考慮了該客戶的年齡、收入和購買歷史等特征后，模型預測該客戶購買產品的概率為 0.65。?
四、shap_values?數組
SHAP 旨在深入剖析模型對單個樣本做出預測的內在原因。對于每個樣本的預測，需要明確每個特征對預測值的作用方向（是使預測值升高還是降低）以及作用程度（升高或降低了多少）。SHAP 值直觀地反映了特征對樣本預測值的 “推力”，SHAP 值的絕對值越大，說明該特征對預測值的影響越顯著。
回歸問題：
模型輸出特點：回歸模型的輸出是一個連續的數值，例如預測房價、溫度等。
計算邏輯：對于數據集中的每個樣本（共n_samples個），都要計算每個特征（共n_features個）對該樣本預測值的 SHAP 值。
數組結構：shap_values生成的是一個numpy數組，它的形狀為 (n_samples, n_features)。例如，shap_values[10, 3] 表示第 10 個樣本的第 3 個特征對該樣本預測值的貢獻。
即：shap_values.shape = (n_samples, n_features)
分類問題：
模型輸出特點：分類模型通常為每個類別輸出一個分數或概率，例如在判斷一封郵件是垃圾郵件還是正常郵件時，模型會給出郵件屬于垃圾郵件和正常郵件的概率。
計算邏輯：SHAP 需要分別解釋模型是如何得出每個類別的分數的。所以對于每個樣本，要針對每個類別分別計算每個特征的 SHAP 值。
數組結構：常見的組織方式是返回一個列表，列表長度等于類別數。列表的第 k 個元素是一個 (n_samples, n_features) 的numpy數組，表示所有樣本的所有特征對預測類別k的貢獻。
即：shap_values.shape =(n_samples, n_features, n_classes)
例如二分類問題中，shap_values[0][10, 3] 表示第 10 個樣本的第 3 個特征對該樣本被預測為第 0 類的貢獻；shap_values[1][10, 3] 則表示第 10 個樣本的第 3 個特征對該樣本被預測為第 1 類的貢獻。
總結：
SHAP 通過計算 Shapley 值，將模型預測分解到每個特征上，這種分解針對每個樣本、每個特征以及分類問題中的每個類別都要進行，從而形成了特定結構的shap_values數組。通過這個數組，我們能夠清晰地了解模型預測背后每個特征的作用，為模型解釋提供了有力的工具。
五、代碼實例
import shap
import matplotlib.pyplot as plt# 初始化 SHAP 解釋器，他會分析模型結構，為后續計算shap值做準備
explainer = shap.TreeExplainer(rf_model)# 計算 SHAP 值（測試集），這個計算耗時
shap_values = explainer.shap_values(X_test)# 生成所有特征對每個樣本預測結果的影響程度
shap_values
array表示不同類別，每行表示單個樣本，每列表示單個特征，值表示特征對樣本預測結果的影響程度，正值表示正向影響，負值表示負向影響。
注意！！！分類問題返回的是列表，列表沒有shape屬性，所以會報錯：
將列表轉化為數組，形狀為(num_classes, n_samples, n_features)
shap_array = np.array(shap_values)
#根據索引對維度進行轉置，變成 (n_samples, n_features, num_classes)
shap_array_aligned = np.transpose(shap_array, axes=(1, 2, 0))
shap_array_aligned.shape
# 輸出：（1500,31,2）?
print("shap_array_aligned shape:", shap_array_aligned.shape)
print("shap_array_aligned[0] shape:", shap_array_aligned[0].shape)
print("shap_array_aligned[:, :, 0] shape:", shap_array_aligned[:, :, 0].shape)
print("X_test shape:", X_test.shape)
# 輸出：
shap_array_aligned shape: (1500, 31, 2)
shap_array_aligned[0] shape: (31, 2)
shap_array_aligned[:, :, 0] shape: (1500, 31)
X_test shape: (1500, 31)shap_array_aligned[:, :, 0] ：
第一個 : 表示選取第一個維度（樣本維度）上的所有元素。
第二個 : 表示選取第二個維度（特征維度）上的所有元素。
0 表示選取第三個維度（類別維度）上索引為 0 的元素。
shap_array_aligned 的形狀是 (n_samples, n_features, num_classes)，經過這個切片操作后，會得到一個新的二維數組，其形狀為 (n_samples, n_features)。這個新數組包含了所有樣本的所有特征對于類別索引為 0 的 SHAP 值。
在處理多維數組切片時，start:stop:step 這種格式中 step 用于指定步長，即每隔多少個元素取一個。但當只寫一個數字，如這里的 0，它就被當作索引，用來精確獲取指定位置的元素。 如果想要在第三個維度上使用步長，格式會變為 shap_array_aligned[:, :, ::2]，這表示在第三個維度上，從開頭開始，每隔一個元素（步長為 2）進行選取。
上面這些輸出有點玄學，不同電腦可能輸出不同，中間的2個誰和x_test的尺寸一樣就選誰
特征重要性條形圖
print("--- 1. SHAP 特征重要性條形圖 ---")
# show=False表示不立即顯示圖形,這樣可繼續用plt自定義修改圖形
shap.summary_plot(shap_array_aligned[:, :, 0], X_test, plot_type="bar",show=False)
plt.title("SHAP Feature Importance (Bar Plot)")
plt.show()
mean(|SHAP value|) ： 取絕對值 |SHAP value| 是為了消除特征影響的正負方向差異，只關注影響的大小幅度，這里關注的是影響程度本身。 計算均值 mean 是對所有樣本的 |SHAP value| 進行平均 ，得到的結果反映了該特征在整個數據集上對模型輸出結果幅度的平均影響程度。均值越大，說明該特征在模型預測中越重要。?
特征重要性蜂巢圖
print("--- 2. SHAP 特征重要性蜂巢圖 ---")
shap.summary_plot(shap_array_aligned[:, :, 0], X_test,plot_type="violin",show=False,max_display=10)
# max_display=10 表示只顯示對預測結果影響最大的前 10 個特征，默認為20.
plt.title("SHAP Feature Importance (Violin Plot)")
plt.show()
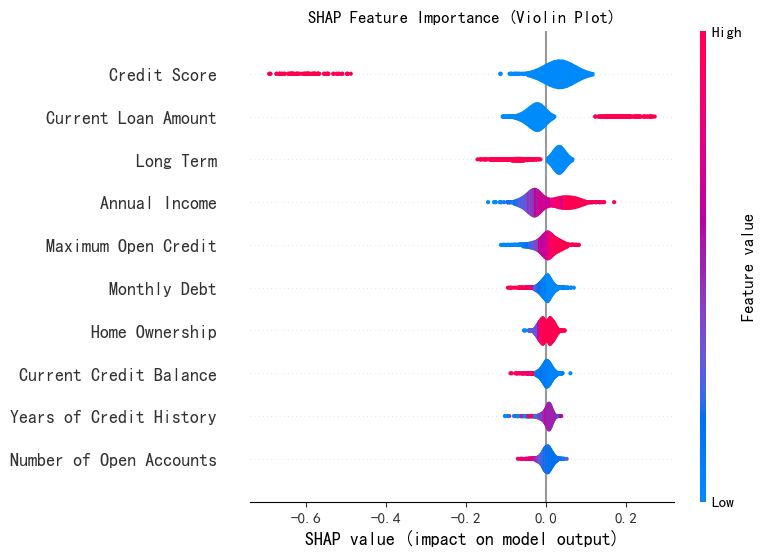?注意！！！小提琴圖的橫軸表示單個樣本中特征的shap值，和條形圖橫軸表示特征在所有樣本的特征平均值。
假設我們有一個包含 1000 個樣本的數據集，在繪制 “信用評分” 這個特征的小提琴圖時，橫軸會涵蓋這 1000 個樣本中 “信用評分” 特征各自對應的 SHAP 值。小提琴圖會展示出這 1000 個 SHAP 值是如何分布的，是集中在正值區域還是負值區域，是分布得比較分散還是相對集中等信息。
六、閱讀材料：
SHAP 可視化解釋機器學習模型簡介_shap圖-CSDN博客
@浙大疏錦行
