二叉樹的遍歷與構造

唉，好想回家，我想回家跟饅頭醬玩，想老爸老媽。如果上天再給我一次選擇的機會，我會選擇當一只小動物，或者當棵大樹也好，或者我希望自己不要有那么多多余的情緒，不要太被別人影響，開心點，想睡就睡，想玩就玩，不要為難自己。老爸每次都和我說累了就回家，但越是這樣我就越希望自己變得更強大一點。希望明天是個好天氣。

一、遍歷

1 前序遍歷

（1）遞歸

（2）非遞歸（先右后左哈）

2 中序遍歷

（1）遞歸

（2）非遞歸

3 后序遍歷

（1）遞歸

（2）非遞歸（中右左，反轉列表后變成左右中）

4 層序遍歷

（1）bfs（借助隊列）

（2）dfs

二、構造

1 構建最大二叉樹

2 由前中構造

3 由前?后構造

4 由?中后構造

一、遍歷

1 前序遍歷

（1）遞歸

   private static void preorderHelper(TreeNode node, List<Integer> result) {if (node == null) return;result.add(node.val);preorderHelper(node.left, result);preorderHelper(node.right, result);}

（2）非遞歸（先右后左哈）

// 前序遍歷 - 非遞歸public static List<Integer> preorderTraversalIterative(TreeNode root) {List<Integer> result = new ArrayList<>();if (root == null) return result;Stack<TreeNode> stack = new Stack<>();stack.push(root);while (!stack.isEmpty()) {TreeNode node = stack.pop();result.add(node.val);if (node.right != null) stack.push(node.right);if (node.left != null) stack.push(node.left);}return result;}

2 中序遍歷

（1）遞歸

 private static void inorderHelper(TreeNode node, List<Integer> result) {if (node == null) return;inorderHelper(node.left, result);result.add(node.val);inorderHelper(node.right, result);}

（2）非遞歸

核心思路是先將當前節點及其所有左子節點依次入棧，直到左子節點為空，接著從棧中彈出節點進行訪問，然后將當前節點更新為彈出節點的右子節點，繼續重復上述操作。

// 中序遍歷 - 非遞歸public static List<Integer> inorderTraversalIterative(TreeNode root) {List<Integer> result = new ArrayList<>();Stack<TreeNode> stack = new Stack<>();TreeNode current = root;while (current != null || !stack.isEmpty()) {while (current != null) {stack.push(current);current = current.left;}current = stack.pop();result.add(current.val);current = current.right;}return result;}

3 后序遍歷

（1）遞歸

private static void postorderHelper(TreeNode node, List<Integer> result) {if (node == null) return;postorderHelper(node.left, result);postorderHelper(node.right, result);result.add(node.val);}

（2）非遞歸（中右左，反轉列表后變成左右中）

 // 后序遍歷 - 非遞歸public static List<Integer> postorderTraversalIterative(TreeNode root) {List<Integer> result = new ArrayList<>();if (root == null) return result;Stack<TreeNode> stack = new Stack<>();stack.push(root);while (!stack.isEmpty()) {TreeNode node = stack.pop();result.add(node.val);if (node.left != null) stack.add(node.left);if (node.right != null) stack.add(node.right);}Collections.reverse(result);return result;}

4 層序遍歷

（1）bfs（借助隊列）

 // 層序遍歷 - BFS（借助隊列）public static List<List<Integer>> levelOrderTraversalBFS(TreeNode root) {List<List<Integer>> result = new ArrayList<>();if (root == null) return result;Queue<TreeNode> queue = new LinkedList<>();queue.offer(root);while (!queue.isEmpty()) {int levelSize = queue.size();List<Integer> level = new ArrayList<>();for (int i = 0; i < levelSize; i++) {TreeNode node = queue.poll();level.add(node.val);if (node.left != null) queue.offer(node.left);if (node.right != null) queue.offer(node.right);}result.add(level);}return result;}

（2）dfs

 // 層序遍歷 - DFSpublic static List<List<Integer>> levelOrderTraversalDFS(TreeNode root) {List<List<Integer>> result = new ArrayList<>();dfs(root, 0, result);return result;}private static void dfs(TreeNode node, int level, List<List<Integer>> result) {if (node == null) return;if (level >= result.size()) {result.add(new ArrayList<>());}result.get(level).add(node.val);dfs(node.left, level + 1, result);dfs(node.right, level + 1, result);}

二、構造

1 構建最大二叉樹

給定一個不重復的整數數組 nums 。最大二叉樹可以用下面的算法從 nums 遞歸地構建:

創建一個根節點，其值為 nums 中的最大值。
遞歸地在最大值左邊的子數組前綴上構建左子樹。
遞歸地在最大值右邊的子數組后綴上構建右子樹。
返回 nums 構建的最大二叉樹

輸入：nums = [3,2,1,6,0,5]
輸出：[6,3,5,null,2,0,null,null,1]
解釋：遞歸調用如下所示：

[3,2,1,6,0,5] 中的最大值是 6 ，左邊部分是 [3,2,1] ，右邊部分是 [0,5] 。
[3,2,1] 中的最大值是 3 ，左邊部分是 [] ，右邊部分是 [2,1] 。
空數組，無子節點。
[2,1] 中的最大值是 2 ，左邊部分是 [] ，右邊部分是 [1] 。
空數組，無子節點。
只有一個元素，所以子節點是一個值為 1 的節點。
[0,5] 中的最大值是 5 ，左邊部分是 [0] ，右邊部分是 [] 。
只有一個元素，所以子節點是一個值為 0 的節點。
空數組，無子節點。

解法&思路

首先要解決的是找到每次遞歸傳入數組的最大值做為根節點
該最大值下標左邊的元素遞歸構造為左子樹，右邊的元素遞歸構造為右子樹

// 定義二叉樹節點類
class TreeNode {int val;TreeNode left;TreeNode right;TreeNode() {}TreeNode(int val) { this.val = val; }TreeNode(int val, TreeNode left, TreeNode right) {this.val = val;this.left = left;this.right = right;}
}class Solution {public TreeNode constructMaximumBinaryTree(int[] nums) {return build(nums, 0, nums.length);}private TreeNode build(int[] nums, int start, int end) {// 如果數組為空，返回 nullif (start == end) {return null;}// 找到最大值和最大值的索引int maxIndex = start;for (int i = start + 1; i < end; i++) {if (nums[i] > nums[maxIndex]) {maxIndex = i;}}// 用最大值創建根節點TreeNode rootNode = new TreeNode(nums[maxIndex]);// 最大值左側為左子樹rootNode.left = build(nums, start, maxIndex);// 最大值右側為右子樹rootNode.right = build(nums, maxIndex + 1, end);return rootNode;}
}

2 由前中構造

// 定義二叉樹節點類
class TreeNode {int val;TreeNode left;TreeNode right;TreeNode() {}TreeNode(int val) { this.val = val; }TreeNode(int val, TreeNode left, TreeNode right) {this.val = val;this.left = left;this.right = right;}
}class Solution {public TreeNode buildTree(int[] preorder, int[] inorder) {return build(preorder, inorder, 0, 0, inorder.length - 1);}private TreeNode build(int[] preorder, int[] inorder, int preStart, int inStart, int inEnd) {// 如果中序遍歷的起始下標大于結束下標，說明當前子樹為空if (inStart > inEnd) {return null;}// 從前序遍歷中找到根節點int rootVal = preorder[preStart];TreeNode rootNode = new TreeNode(rootVal);// 在中序遍歷中找到根節點的位置int rootIndex = -1;for (int i = inStart; i <= inEnd; i++) {if (inorder[i] == rootVal) {rootIndex = i;break;}}// 計算左子樹的大小int leftSize = rootIndex - inStart;// 遞歸構造左子樹// 左子樹的前序遍歷范圍：preStart + 1 到 preStart + leftSize// 左子樹的中序遍歷范圍：inStart 到 rootIndex - 1rootNode.left = build(preorder, inorder, preStart + 1, inStart, rootIndex - 1);// 遞歸構造右子樹// 右子樹的前序遍歷范圍：preStart + leftSize + 1 到 preStart + leftSize + 右子樹大小// 右子樹的中序遍歷范圍：rootIndex + 1 到 inEndrootNode.right = build(preorder, inorder, preStart + leftSize + 1, rootIndex + 1, inEnd);return rootNode;}
}

至于為什么只需要中序遍歷的終點，而不需要前序遍歷的終點？因為在我們的思路中其實可以發現只需要前序遍歷的起點確認根節點的值，并不需要終點值。我們可以隨便選擇一個遍歷的終點值用來確認邊界值，即這部分代碼。

if(inStart > inEnd){return null
}

3 由前?后構造

// 定義二叉樹節點類
class TreeNode {int val;TreeNode left;TreeNode right;TreeNode() {}TreeNode(int val) { this.val = val; }TreeNode(int val, TreeNode left, TreeNode right) {this.val = val;this.left = left;this.right = right;}
}class Solution {public TreeNode constructFromPrePost(int[] preorder, int[] postorder) {return build(preorder, 0, preorder.length - 1, postorder, 0, postorder.length - 1);}private TreeNode build(int[] preorder, int preStart, int preEnd, int[] postorder, int postStart, int postEnd) {// 如果前序遍歷的起始下標大于結束下標，說明當前子樹為空if (preStart > preEnd) {return null;}// 當前子樹只有一個節點時，直接返回該節點if (preStart == preEnd) {return new TreeNode(preorder[preStart]);}// 找到根節點int rootVal = preorder[preStart];TreeNode root = new TreeNode(rootVal);// 找到左子樹起點在后序遍歷中的位置int leftStartIndex = -1;for (int i = postStart; i <= postEnd; i++) {if (postorder[i] == preorder[preStart + 1]) {leftStartIndex = i;break;}}// 計算左子樹的長度int size = leftStartIndex - postStart + 1;// 遞歸構造左子樹// 左子樹的前序范圍：preStart + 1 到 preStart + size// 左子樹的后序范圍：postStart 到 leftStartIndexroot.left = build(preorder, preStart + 1, preStart + size, postorder, postStart, leftStartIndex);// 遞歸構造右子樹// 右子樹的前序范圍：preStart + size + 1 到 preEnd// 右子樹的后序范圍：leftStartIndex + 1 到 postEnd - 1root.right = build(preorder, preStart + size + 1, preEnd, postorder, leftStartIndex + 1, postEnd - 1);return root;}
}

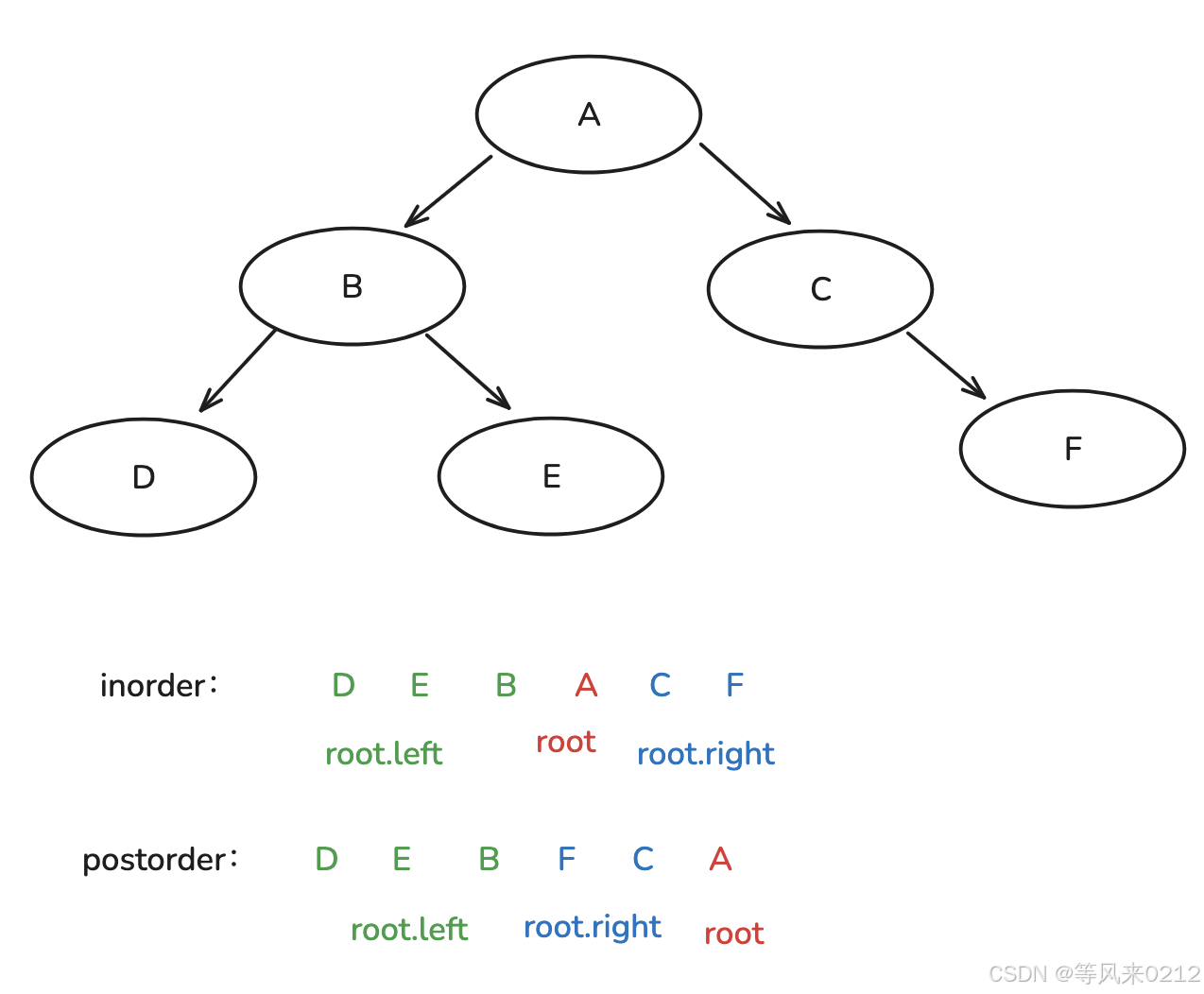
4 由?中后構造

// 定義二叉樹節點類
class TreeNode {int val;TreeNode left;TreeNode right;TreeNode() {}TreeNode(int val) { this.val = val; }TreeNode(int val, TreeNode left, TreeNode right) {this.val = val;this.left = left;this.right = right;}
}class Solution {public TreeNode buildTree(int[] inorder, int[] postorder) {return build(inorder, 0, inorder.length - 1, postorder, 0, postorder.length - 1);}private TreeNode build(int[] inorder, int inStart, int inEnd, int[] postorder, int postStart, int postEnd) {// 如果中序遍歷的起始下標大于結束下標，說明當前子樹為空if (inStart > inEnd) {return null;}// 后序遍歷的最后一個節點是根節點int rootVal = postorder[postEnd];TreeNode rootNode = new TreeNode(rootVal);// 找到根節點在中序遍歷中的位置int rootIndex = -1;for (int i = inStart; i <= inEnd; i++) {if (inorder[i] == rootVal) {rootIndex = i;break;}}// 計算左子樹的大小int leftSize = rootIndex - inStart;// 遞歸構造左子樹// 左子樹的中序范圍：inStart 到 rootIndex - 1// 左子樹的后序范圍：postStart 到 postStart + leftSize - 1rootNode.left = build(inorder, inStart, rootIndex - 1, postorder, postStart, postStart + leftSize - 1);// 遞歸構造右子樹// 右子樹的中序范圍：rootIndex + 1 到 inEnd// 右子樹的后序范圍：postStart + leftSize 到 postEnd - 1rootNode.right = build(inorder, rootIndex + 1, inEnd, postorder, postStart + leftSize, postEnd - 1);return rootNode;}
}