數據結構之哈夫曼樹

8.哈夫曼樹

8.1 哈夫曼編碼

哈夫曼編碼（Huffman Coding），又稱霍夫曼編碼，是一種可變字長編碼（VLC）方式

這種編碼方法完全依據字符出現的概率來構造異字頭的平均長度最短的碼字，因此有時也被稱為最佳編碼。

基本原理

有5個字符a b c d e要發送

a出現10次 b： 5 c： 3 d：20 f：1

如果發送的要快就要保證編碼盡量短，這樣就要求頻率高的編碼長度短，頻率低的編碼長度可以長一點。
基本步驟：
- 計算字符頻率：首先，統計每個字符在數據中出現的頻率（次數）。
- 構建哈夫曼樹：根據字符的頻率，使用自底向上的方法構建一棵哈夫曼樹。在構建過程中，將頻率最低的兩個節點合并為一個新的節點，其頻率為兩者之和，并將這兩個字符分別作為新節點的左右子節點。然后，將新節點加入到未處理的字符列表中，繼續重復此過程，直到所有字符都被合并到一個根節點下
  - 為什么選擇最低的兩個節點？
    - 因為頻率最低路徑也越長，編碼長度也長
    - 通信原理里面可能少的比特數傳輸盡可能多的信息，以提高通信效率。將頻率低的信號編碼為較長的碼字，可以使得頻率高的信號占用較少的比特數，從而整體上減少傳輸的數據量
- 生成編碼：從根節點開始，為樹中的每個字符生成一個唯一的編碼
  
  對于每個非葉子節點，將其左子節點的連接線標記為“0”，右子節點的連接線標記為“1”。字符的編碼即為從根節點到該字符葉子節點路徑上的所有“0”和“1”的序列

特點：

高效性：由于字符編碼的長度與其在數據中出現的頻率成反比，因此高頻字符使用較短的編

碼，而低頻字符使用較長的編碼，從而實現了數據的高效壓縮。
唯一性：哈夫曼編碼的碼字是異前置碼字，即任一碼字不會是另一碼字的前面部分（因為父節

點是子節點的和），這使得各碼字可以連在一起傳送，中間不需另加隔離符號。
不唯一性：雖然哈夫曼樹和編碼的帶權路徑長度是唯一的，但哈夫曼樹和編碼本身并不唯一。

在構建哈夫曼樹時，如果兩個字符的頻率相等，它們可以以不同的順序合并，從而導致不同的

哈夫曼樹和編碼。
應用場景
文件和數據壓縮：哈夫曼編碼可用于文本、圖像、音頻等各種類型文件的壓縮，通過減少文件

大小來節省存儲空間。
通信傳輸：在網絡傳輸中，使用哈夫曼編碼可以減小數據的大小，從而減少網絡帶寬的占用，

加快數據傳輸速度。
無損壓縮文件格式：GZIP、PKZIP、PNG和JPEG等文件格式都使用哈夫曼編碼對文件中的數

據進行壓縮。
文本處理：在自然語言處理、文本挖掘等領域，哈夫曼編碼可用于生成文本的索引、單詞頻率

統計和特征向量表示等任務。

8.2 哈夫曼樹

定義

哈夫曼樹，也稱為最優二叉樹或最小帶權路徑長度樹，是一種特殊的二叉樹結構，其主要特點是帶權路徑長度最短。

給定N個權值（頻率/次數）作為N個葉子結點，構造一棵二叉樹，若該樹的帶權路徑長度達到最小，則稱這樣的二叉樹為最優二叉樹，也稱為哈夫曼樹。

帶權路徑長度（WPL）

樹中所有的葉結點的權值乘上其到根結點的路徑長度（若根結點為0層，葉結點到根結點的路徑長度為葉結點的層數）。計算公式為WPL = Σ(Wi * Li)，其中Wi表示葉子結點ki的權值，Li表示根結點到葉子結點 ki的路徑長度

實際中權可能是金錢、時間成本等等

構造哈夫曼樹

哈夫曼樹的構造過程是自底向上的，步驟：

示例：已知字符集{ a, b, c, d, e, f }，若各字符出現的次數分別為{ 6, 3, 8, 2, 10, 4 }

初始化：將給定的N個權值視為N棵只有根結點的二叉樹（即葉子結點），這些二叉樹構成初始森林。

每個節點都當成一個樹（樹構成森林）
選擇合并：在森林中選取兩棵根結點的權值最小的樹作為左右子樹，構造一棵新的二叉樹，且置新的二叉樹的根結點的權值為其左右子樹上根結點的權值之和。

找兩森林中兩個權值最小的樹，即b（3）和d（2）為左右子樹，根節點的權值是二者之和
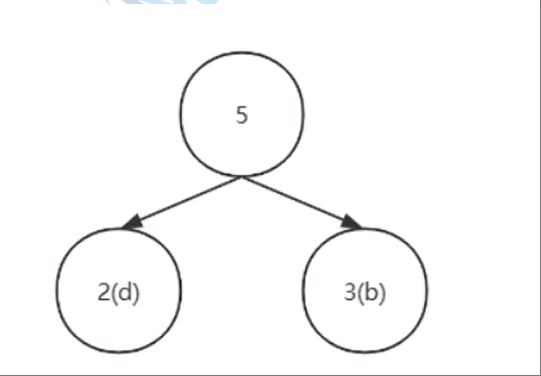
更新森林：在初始森林中刪除這兩棵樹，同時將新得到的二叉樹加入森林中**(左小右大**)。
重復操作：重復上述兩個步驟，直到森林中只剩下一棵樹為止。

再選出2個最小的數，選出了4（f）和5（上述步驟中組合后的父節點）

在這里插入圖片描述

此時該森林中就有4棵樹（a, c, e）以及上述圖片中的樹，權值分別為（6, 8, 10 ）

再選出2個最小的數，選出了6（a）和8（c）

在這里插入圖片描述

此時該森林中就有3棵樹（e）以及上述圖片中兩棵樹的樹，權值分別為（10 ）再選出2個最小的數，選出了9和10（e）

在這里插入圖片描述

此時該森林中就只有有上述圖片中兩棵樹的樹

將兩棵樹合并為一棵樹

在這里插入圖片描述

這棵樹便是哈夫曼樹。

哈夫曼編碼

從根節點開始向下走往左為0，往右1。走到對應的字符的路徑就是該字符的哈夫曼編碼（左0右1）

在這里插入圖片描述

最終的哈夫曼編碼左0 右1

高頻字符使用較短的編碼，而低頻字符使用較長的編碼

字符權值 哈夫曼編碼

a 6 00

b 3 1011

c 8 01

d 2 1010

e 10 11

f 4 100

#include <iostream>
#include <queue>
using namespace std;
// 哈夫曼樹的節點（一個節點表示一棵樹）
typedef struct  Node
{int weight; //權值struct  Node *left; //左孩子struct  Node *right;//右孩子
}TreeNode;// 哈夫曼樹（(通過樹表示森林)）
typedef struct  HumanTree
{// 樹的根節點 通過這個根節點可以訪問整棵樹的所有節點Node *root;//下一個樹，通過鏈表把樹連起來變成森林struct HumanTree *nextTree;
}HumanTree;// 創建節點
Node *createNode(int weight)
{//分配內存Node *newNode = new Node{weight};// 初始化newNode->left =nullptr;newNode->right = nullptr;return newNode;
}// 創建哈夫曼樹
HumanTree *createHumanTree(Node *root)
{// 變量名不能和類型名相同HumanTree *newTree = new HumanTree; // 初始化newTree->root = root;newTree->nextTree = nullptr;return newTree;
}//森林插入新樹
void insertTree(HumanTree **tree, HumanTree *newtree)//第一個是森林 第二個是新樹 因為森林會插入新樹數量會修改，如果使用二級指針
{// 森林是空,森林就是新樹if(!*tree){(*tree) = newtree;return;}// 中間節點指針 從第一顆樹開始遍歷HumanTree *current = (*tree);// 循環 使用current->nextTree和鏈表一樣,如果是current到了null無法返回尾樹了  while(current->nextTree){current = current->nextTree;}// 尾數處插入新樹current->nextTree = newtree;}// 從森林中刪除某棵樹（并非真正刪除，而是合并了）
void deleteTree(HumanTree **tree, HumanTree *deletetree)
{// 如果刪除的是第一課樹 頭樹if((*tree)->root->weight == deletetree->root->weight ){(*tree) =(*tree)->nextTree;delete deletetree;deletetree = nullptr;return;}// 不是第一顆樹 遍歷HumanTree *currentTree = (*tree);while(currentTree->nextTree){// 找到了要刪除的樹  currentTreeif(currentTree->nextTree->root->weight == deletetree->root->weight){// 更新森林currentTree->nextTree = currentTree->nextTree->nextTree;delete deletetree;deletetree = nullptr;return;}currentTree = currentTree->nextTree;}
}// 選擇合并  在森林中選取兩棵根結點的權值最小的樹，構造一棵新的二叉樹 會改變樹的結構 用**
bool selectMerge(HumanTree **tree)
{// 空樹或者只有一個節點if(!(*tree) || !(*tree)->nextTree){return false;}// 1. 找到權重最小的兩棵樹HumanTree *minTree1 = nullptr;//最小HumanTree  *minTree2 =nullptr;//第二小// 先從森林里找到前兩棵來為最小的兩棵樹初始化if((*tree)->root->weight < (*tree)->nextTree->root->weight)//判斷先兩顆樹誰打誰小{minTree1 = (*tree);minTree2 = (*tree)->nextTree;}else{minTree1 = (*tree)->nextTree;minTree2 = (*tree);}//   2.當前樹（從第三棵樹開始與前兩棵書比較）   // 存儲第三個節點HumanTree *current = (*tree)->nextTree->nextTree;// 比這個樹都小while(current){// 比最小的小 之前最小的變成第二項，當前的變成最小if(current->root->weight < minTree1->root->weight){// 更新倒數第二小minTree2 = minTree1;// 更新最小minTree1 =  current;}// 比最二的小，最小的大 else if(current->root->weight < minTree2->root->weight && current->root->weight > minTree1->root->weight){// 更新倒數第二小minTree2 = current;}// 往后訪問current = current->nextTree;}// 2. 合并這兩棵樹//  創建父節點 存儲這兩個節點(最小和第二小)TreeNode *newTreeNode =  createNode(minTree1->root->weight + minTree2->root->weight);//  創建新樹 參數是新的父節點HumanTree *newTree = createHumanTree(newTreeNode);// 左小右大 將兩棵樹合并為一顆新樹newTree->root->left = minTree1->root;newTree->root->right = minTree2->root;// 3. 將新樹插入到森林insertTree(tree, newTree);//4. 刪除原來的兩棵樹deleteTree(tree, minTree1);deleteTree(tree, minTree2);return true;
}// 打印哈夫曼編碼
void printTree(TreeNode *p_code, string& code) // 傳入節點   code是為其添加0 1
{// 空樹if(!p_code){return;}//葉子節點，則打印字符和對應的編碼if(p_code->left == nullptr && p_code->right == nullptr){cout << p_code->weight << ":"  << code << endl;}// 遞歸地遍歷左右子樹，并在當前編碼的基礎上添加'0'或'1'else{string leftNode = code + "0";string rightNode = code + "1";printTree( p_code->left, leftNode);printTree( p_code->right, rightNode);}
}// 清理函數(左右根)
void deintTree(TreeNode *node)
{if(!node ){return;}deintTree(node->left);deintTree(node->right);delete node;
}// 層次遍歷（隊列（一層一層遍歷）
void levelPrint(HumanTree *p_tree)
{if(!p_tree){cout << "空樹" << endl;return;}// 創建隊列，存儲樹中每個節點 先進先出，符合層次遍歷queue <TreeNode*>  q;// 先存儲根節點q.push(p_tree->root);while(!q.empty()){// 保存根節點信息TreeNode *current = q.front();//一直保存根節點// 彈出根節點q.pop();// 訪問當前節點cout.width(2);cout << current->weight << " ";// 如果左子節點存在，則加入隊列if(current->left){q.push(current->left);}// 如果右子節點存在，則加入隊列if(current->right){q.push(current->right);}}cout << endl;}// 主函數示例
int main()
{// 創建權值int weight[] = {6, 3, 8, 2, 10, 4};// 創建哈夫曼樹HumanTree *newHumanTree  = nullptr;//  創建樹節點for(int i = 0; i < sizeof(weight)/sizeof( weight[0]); i++){// 創建樹并插入森林// insertTree插入樹函數 newHumanTree取地址作為二級指針傳入，是當前森林，createHumanTree是創建樹// createHumanTree參數是節點createNode(weight[i])是創建節點后直接作為參數傳入 createHumanTre中insertTree (&newHumanTree,createHumanTree(createNode(weight[i])));}// 選擇合并while (selectMerge(&newHumanTree));//  // 層次遍歷levelPrint(newHumanTree);// 打印哈夫曼編碼string code = " ";printTree(newHumanTree->root, code);// 銷毀樹內節點deintTree(newHumanTree->root);// 銷毀樹delete newHumanTree;newHumanTree = nullptr;return 0;
}

根節點root是樹的入口，通過它可以訪問整棵樹的所有其他節點*

找了一頓bug結果是 selectMerg if(!(*tree) || !(*tree)->nextTree)空樹或者只有一個節點寫錯了寫成 selectMerg if(!(*tree) || (*tree)->nextTree) 下次注意