目錄
1,小美的平衡矩陣
2,小美的數組詢問
3,小美的MT
?4,小美的朋友關系
1,小美的平衡矩陣

?【題目描述】
給定一個n*n的矩陣,該矩陣只包含數字0和1。對于 每個i(1<=i<=n),求在該矩陣中,有多少個i*i的區域滿足0的個數等于1的個數???
【題目解析】
示例演示:
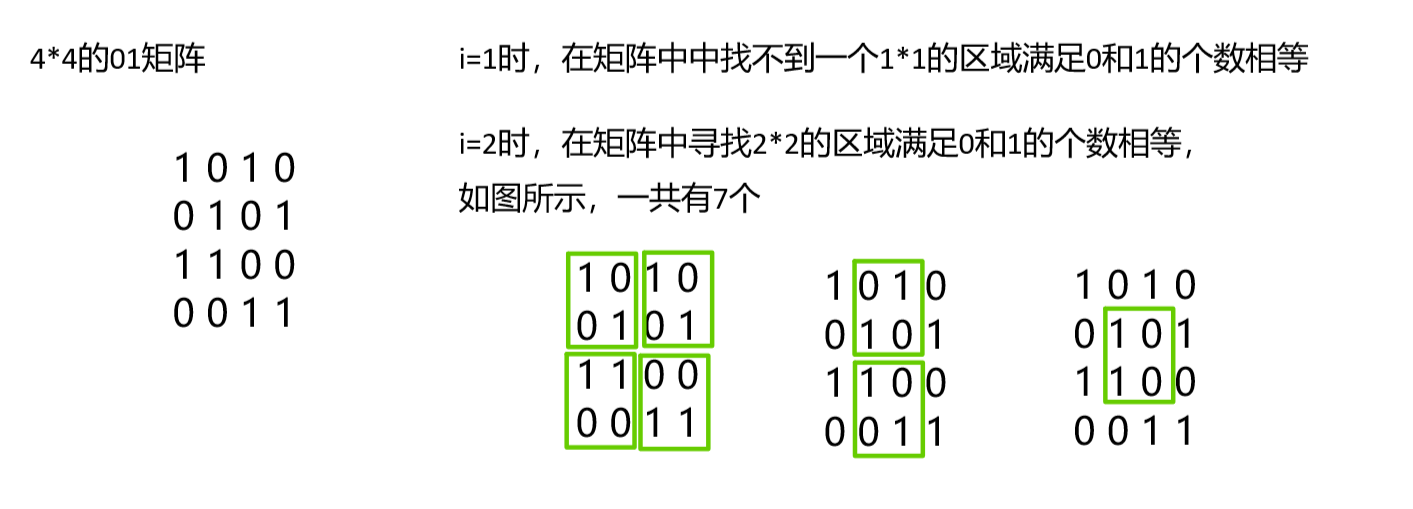
?如上圖,1*1的區域結果為0,2*2的區域結果為7。
算法:前綴和+遍歷
題目中給的數據范圍是n<=200,所以可以直接遍歷數組。
維護 一個前綴和數組統計以(x,y)這個點為右下角,以(1,1)這個點為左上角,這個區域中所有元素的和,由于數組中的數要么是0,要么是1,所以前綴和就表示某個區域中1的個數。
有了前綴和數組,就可以快速 求出某個區域中1的個數,如圖:
而這個區域的大小我們是知道的,假設是k,那么這個區域的元素個數就是k*k。如果滿足這個區間中1的個數等于k*k/2,那么說明 這個區間中0和1的個數 相等。而1的個數我們可以通過前綴和來表示。
同時還有一點,如果k為奇數,那么k*k的區域中元素個數一定為奇數 ,所以0和1的個數一定不相等。直接輸出0即可。
?注意:在輸入數據的時候,如果是以整數的形式接受,那么不建議使用cin,因為cin會把第一行的所有數據讀成一個整數。就比如 上面的示例,第一行會被讀成一個整數1010,而我們期望是讀到4個整數的,這是可以使用scanf("%1d",&a),使用 %1d占位符可以確保讀到的第一行是4個整數。
【代碼】
#include <iostream>
#include <vector>
using namespace std;const int N = 205;
int arr[N][N], s[N][N];
//s為前綴和數組
//統計矩形(1,1)到(n,n)中1的數量int main()
{int n = 0;cin >> n;for(int i=1;i<=n;i++)for (int j = 1; j <= n; j++){scanf("%1d", &arr[i][j]);s[i][j] = s[i - 1][j] + s[i][j - 1] - s[i - 1][j - 1] + arr[i][j];}cout << 0 << endl;for (int k = 2; k <= n; k++){if (k & 1){cout << 0 << endl;continue;}int ans = 0;for(int i=1;i+k-1<=n;i++)for (int j = 1; j+k-1 <= n; j++){//(i,j)是左上角,需要我們計算出k*k這個區域右下角的坐標int x = i + k - 1;int y = j + k - 1;if (s[x][y] - s[i - 1][y] - s[x][j - 1] + s[i - 1][j - 1] == k * k / 2)ans++;}cout << ans << endl;}return 0;
}2,小美的數組詢問

?直接遍歷即可?
#include <iostream>
using namespace std;const int N=1e5+10;
int arr[N];
int main()
{int n=0,q=0;cin>>n>>q;long long sum=0,count=0;for(int i=1;i<=n;i++){cin>>arr[i];sum+=arr[i];if(arr[i]==0)count++;}int l,r;while(q--){cin>>l>>r;cout<<sum+count*l<<" "<<sum+count*r<<endl;}return 0;
}3,小美的MT

統計元字符中 有多少個M和T,再加上最多可以修改 多少個即可。
//小美的MT
#include <iostream>
#include <string>
using namespace std;int main()
{int n = 0, k = 0;cin >> n >> k;string str;cin >> str;int ans = 0;for (int i = 0; i < n; i++){if (str[i] == 'M' || str[i] == 'T')ans++;}if (k > n - ans)cout << n << endl;elsecout << ans + k << endl;return 0;
}?4,小美的朋友關系


?【題目描述】
總人數為n,編號u和v的人之間存在朋友關系,在這n個人中,存在m個朋友關系。
對于這些關系,進行q次事件,格式為【op,u,v】,其中u和v表示人的編號。op表示要進行哪種操作,當op==1時,u和v的朋友關系淡忘,也就是斷開u和v的朋友關系。當op==2時,表示查詢u和v是否可以建立朋友關系,可以通過第三方或者本來就是朋友關系。
針對每次的op==2操作,返回一個結果Yes or No,表示是否可以建立朋友關系 。
【思路】
這n個人中存在許多的朋友關系,比如編號1-5是朋友,編號6-10是朋友,這兩個關系是獨立的集合,所以可以想到的是使用并查集來記錄朋友關系。
并查集傳送門:
【算法與數據結構】并查集詳解+題目_并查集結構體-CSDN博客
?并查集中的每個集合可以看成是一棵樹,獨立多個集合,就是多個獨立的樹。每個樹的根節點也就是每個集合的父節點。
剛開始我的思路是將這m個朋友關系,使用并查集來存儲。
但是在q次操作中,op=2是查詢是否可以 建立朋友關系的操作,這個簡單,只需判斷這兩個人是否在同一個集合中,也就是這兩個人的父節點是否相同。但是對于op=1刪除朋友關系操作,比較困難,因為并查集擅于進行 添加關系操作的,不好處理刪除節點關系。所以在刪除朋友關系這里出現了問題。
我們可以試著把刪除朋友關系變成添加朋友關系。這樣并查集就可以做了。那么怎么實現呢?
我們可以先將這m個朋友關系用特定的容器存儲下來,首先遍歷q次操作,遇到刪除操作(u,v),在容器中刪除(u,v)。
注意:這里刪除的時候,要刪除的朋友關系是(u,v),有可能存儲的時候,朋友關系是(u,v),也有可能是(v,u),這些都是要刪除的。
遇到op=2時,不進行操作。一次操作完成后,將該次操作用數組記錄下來【op,u,v】。
順序遍歷完后,此時將容器中剩余的朋友關系,構建并查集。?然后逆序遍歷記錄操作的數組,遇到op=1時,就添加朋友關系,遇到op=2時,就查詢朋友關系,判斷父節點是否相等即可。
?【代碼】
//小美的朋友關系
#include <iostream>
#include <vector>
#include <set>
using namespace std;
const int N = 1e5;//總人數,初始的朋友關系數,事件數量
int n, m, q;
vector<int> parent;//并查集
set<pair<int, int>> st;//存儲初始的朋友關系
//存儲事件
struct node
{int op, u, v;
}arr[N+5];
//找父節點,路徑壓縮
int find(int x)
{if (parent[x] != x)parent[x] = find(parent[x]);return parent[x];
}
//合并
void unite(int x, int y)
{int rootX = find(x);int rootY = find(y);if (rootX == rootY)return;parent[rootX] = rootY;
}
int main()
{cin >> n >> m >> q;//初始化并查集parent.resize(n + 1);for (int i = 1; i <= n; i++)parent[i] = i;//存儲關系int op,u, v;while (m--){cin >> u >> v;st.insert({ u,v });}int num = 0;while (q--){cin >> op >> u >> v;//處理刪除操作if (op == 1){if (st.find({ u,v }) != st.end())st.erase({ u,v });else if (st.find({ v,u }) != st.end())st.erase({ v,u });elsecontinue;//說明u和v表示朋友關系,此次刪除操作無意義,不需要存儲下來}//記錄操作arr[num++] = { op,u,v };}//刪除關系完成后,剩余的元素是沒有進行操作的//構建并查集for (auto [u, v] : st)unite(u, v);vector<bool> ans;//記錄最終結果//逆序遍歷操作//如果是刪除就進行合并//如果是查詢就進行判斷是否在同一個集合for (int i = num - 1; i >= 0; i--){op = arr[i].op, u = arr[i].u, v = arr[i].v;if (op == 1){//合并unite(u, v);}else{//判斷ans.emplace_back(find(u) == find(v));}}for (int i = ans.size() - 1; i >= 0; i--)if (ans[i])cout << "Yes" << endl;elsecout << "No" << endl;return 0;
}
上述代碼是使用vector來實現并查集的,題目中的數據范圍n是1e9,如果使用vector,就需要開辟1e9個空間,會超出內存限制。所以這里實現并查集的時候,需要使用map來替代。存儲當前節點和它的父節點。具體原因,看下方:

初始時,每個節點的父節點就是自己本身。比如mp[1]=1。
當我們逆序遍歷時,當遇到op=2,查詢朋友關系時,給的兩個朋友編號u和v,之前可能沒初始化。比如n=10,給了3個朋友關系(1,3),(3,2),(4,6),當我們查詢的時候,可能查詢的是(5,7),這兩個節點沒有初始化,也就是mp[5]=0,mp[7]=0,可以發現這兩個節點的父節點都是0,如果直接判斷,得到的結果是可以構成朋友關系,但本質是不能構成朋友關系的。
也可以看下方代碼的初始化部分,我們只初始化了存在朋友關系的節點,其他的節點沒有初始化,他們的父節點默認就是0。如果我們開始將所有節點都初始化好,那么就會超出內存限制,那么就和使用vector一樣了,甚至占用的內存比vector還要大,所以我們不能一次性就初始還所有節點。而是當遇到一個沒初始化的節點,就初始化即可。
所以在查詢操作的時候,如果mp[u]=0,或者mp[v]=0,就把這兩個值做一下初始化mp[u]=u或者mp[v]=v,這樣在判斷的時候就不會出錯了。
而如果使用的是vector來表示并查集,是不需要考慮這個問題的,因為vector會開辟n個空間,將所有人都初始化好,父節點就是自己。而使用map來存儲,只會存儲存在朋友關系的節點,如果出現一個新的節點,需要我們自己再初始化。這也就是map不會超出內存限制而vector會超出內存限制的原因。
?【代碼】
//小美的朋友關系
#include <iostream>
#include <vector>
#include <map>
#include <set>
using namespace std;
const int N = 1e5;//總人數,初始的朋友關系數,事件數量
int n, m, q;
map<int,int> parent;//并查集
set<pair<int, int>> st;//存儲初始的朋友關系//存儲事件
struct node
{int op, u, v;
}arr[N + 5];
//找父節點,路徑壓縮
int find(int x)
{if (parent[x] != x)parent[x] = find(parent[x]);return parent[x];
}
//合并
void unite(int x, int y)
{int rootX = find(x);int rootY = find(y);if (rootX == rootY)return;parent[rootX] = rootY;
}
int main()
{cin >> n >> m >> q;//初始化并查集和關系集合int op, u, v;for (int i = 0; i < m; i++){cin >> u >> v;parent[u] = u;parent[v] = v;st.insert({ u,v });}int num = 0;while (q--){cin >> op >> u >> v;//處理刪除操作if (op == 1){if (st.find({ u,v }) != st.end())st.erase({ u,v });else if (st.find({ v,u }) != st.end())st.erase({ v,u });elsecontinue;//說明u和v表示朋友關系,此次刪除操作無意義,不需要存儲下來}//記錄操作arr[num++] = { op,u,v };}//刪除關系完成后,剩余的元素是沒有進行操作的//構建并查集for (auto [u, v] : st)unite(u, v);vector<bool> ans;//記錄最終結果//逆序遍歷操作//如果是刪除就進行合并//如果是查詢就進行判斷是否在同一個集合for (int i = num - 1; i >= 0; i--){op = arr[i].op, u = arr[i].u, v = arr[i].v;if (op == 1){//合并unite(u, v);}else{//parent[u]==0,說明該節點第一次出現,初始化為uif (parent[u] == 0)parent[u] = u;if (parent[v] == 0)parent[v] = v;//判斷ans.emplace_back(find(u) == find(v));}}for (int i = ans.size() - 1; i >= 0; i--)if (ans[i])cout << "Yes" << endl;elsecout << "No" << endl;return 0;
}






:從Airbnb案例看精益創業與數據驅動增長)





:Transformer Reinforcement Learning)





)
上課板書+課件匯總(結構體)-----數據結構常用)