聲明：本人跟隨b站江科大學習，本文章是觀看完視頻后的一些個人總結和經驗分享，也同時為了方便日后的復習，如果有錯誤請各位大佬指出，如果對你有幫助可以點個贊小小鼓勵一下，本文章建議配合原視頻使用??

如果你也正在學習STM32可以訂閱本專欄，后續將不定期更新( ? 3?)??
如有侵權，請私信聯系刪除

---

---

前言

• 這一塊的學習還是得有實踐，不親自感受一下pid調參那么無異于沒學
• 想要制作平衡車的小伙伴建議再去學習一下姿態解算也是很有趣的
• 了解PID每一項的作用以及計算方式很重要
• 優化算法一定要根據實際情況來，不然容易起到反效果
• 串級PID的優點和建立方法要理解
• 調參要懂取舍，多調參才能積累經驗

理論部分

1.PID基本原理

PID簡介

• 做小車就會用到PID算法，因為小車想要走直線就要保證兩個輪子PWM輸出的占空比一致，不一致小車就會走不直，可是你若只考慮輸出相同的占空比，但是還會存在潤滑油多少等外力因素，導致兩個輪子速度肯定不一樣，這時候為了保證速度相同就要使用PID算法

開環與閉環

• 閉環相較于開環相當于多了一個反饋電路形成閉合環路，可根據反饋不斷調節輸出值來接近目標值，開環不會自己調節，輸出一個值后就定死了，哪怕被控對象受外部因素而偏離目標值，輸出值仍然不會自我調整

2.PID算法原理

• 看這個圖就知道PID是一種基于誤差調控的算法，PID的目的是讓誤差為0
• 第二個輸出值公式更為常用，因為分別調節三個參數可以改變三項的值，便于調參，K_p,K_i,K_d是每一項的權重

比列項

• K_p*error(t)就是系統調控的力度，假如error(t)=10，單位可能是速度轉速等等，那么K_p給0.1的話，調控力度就是1，給1的話力度就是10，依次類推，所以K_p不能太大了，否則誤差只要變化很小，比列這一項就會猛的一調，也就是超調，太小的話也不行系統響應會很慢
• 但是不能只有比列這一項用于調節輸出值，會存在穩態誤差
  
• 紅色線條表示電機目標速度，紫色線條是電機實際速度
• 紅色框框表示超調，藍色差值表示穩態誤差，穩定后的實際速度與目標速度的差值
• 這個圖就是只看P比例項的波形圖，可以看到K_p越大紅色框框的超調就越大
• 按理來說只要存在誤差P就會一直進行調節，那為什么會有穩態誤差呢？先看看下面對穩態誤差的介紹

穩態誤差

• 在理想情況時不存在穩態誤差，但是由于電機旋轉必然存在摩擦力，PID最終目的是誤差為0，但是誤差為0時我們的P項輸出也為0，PID的輸出結果直接送到了PWM的輸出函數，也就是PWM輸出為0了，電機也就沒有驅動力不在轉動，由于摩擦力肯定會減速，一旦減速就會有誤差，PID又要開始加速，也就是PWM輸出又會增加，驅動力也會增加，直到驅動力等于摩擦力時系統達到穩態
• 可能有人會問當驅動力和摩擦力達到平衡時，穩態的值還沒達到目標值，難道系統系統看不到嗎，不會繼續增大PWM嗎？但是由于P項過后誤差已經很小了，算法得出的結論是我提供這么多驅動力就夠了，但是系統不知道有摩擦力這么個東西，導致提供的驅動力一直達不到目標值，也沒人告訴他驅動力已經和摩擦力平衡了需要繼續增大驅動力，所以才需要其他項來幫助PID算法
• 積分項就是用于幫助消除穩態誤差的，因為比列項輸出值僅取決于當前誤差，與歷史時刻誤差無關，這意味你想實現使用當前誤差產生的占空比，并在此基礎上加上比例項的輸出作為新的占空比（這樣誤差為正必然加大占空比加速，為負必然減小占空比減速）是行不通的，或者說這其實是積分項的任務

積分項

• 積分項用于消除穩態誤差，也就是提醒系統你的驅動力用來平衡摩擦力了，還得更努力增大驅動力才能達到目標值
• 寫積分項程序要單獨定義一個變量存儲歷史誤差，誤差不斷累計并求和然后乘以一個積分系數得到積分項的輸出
• 積分項不斷累積使其控制力度越來越大，直到能夠讓電機占空比變大，最終達到目標值消除穩態誤差
• 積分項的弊端就是系統滯后性：也就是當系統穩態誤差消除后，此時突然要求電機反轉，那么先要不斷反向積分來消除正向的驅動力，然后再繼續累計使其反轉
• 比列項相對于積分項來說變化非常快，因為只用考慮當前時刻，你說正就是正，你說負就是負，系統響應很快

微分項

• 微分項不會消除誤差
• 主要作用是防止超調，阻止變化過快，提前調控
• 打個比方，平衡車如果只有PI項很難穩定立起來，因為倒下太快了，PI來不及做出調整讓重新平衡，D項的作用就是讓他到下更慢一點，這是PI有更多時間調整
• 缺點就是微分系數過大時會卡頓，因為D項權重太大，導致PI想發生變化時,D項想讓變化慢一點，阻止了PI產生的變化，導致卡頓
  
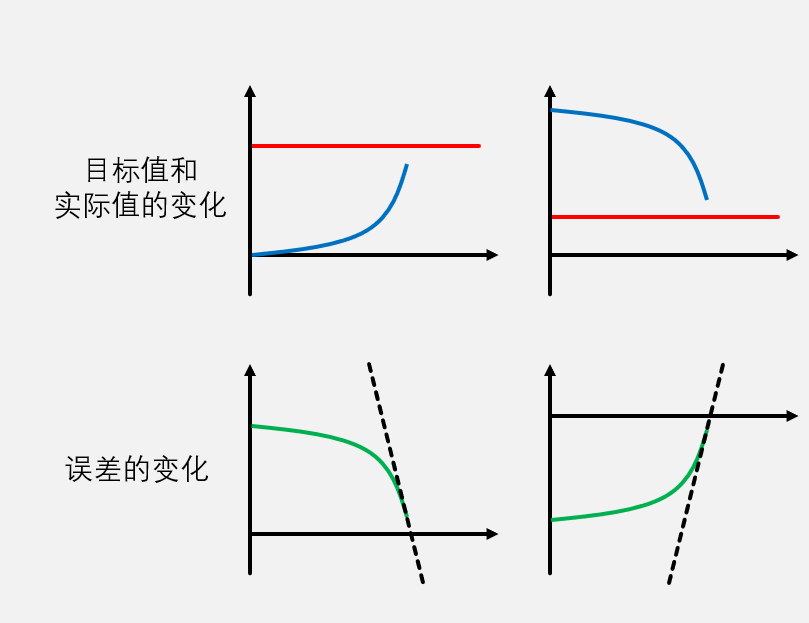
• 藍色曲線為實際值，紅色為目標值，綠色為誤差值（紅色-藍色）
• 上面兩個中藍線都是越接近目標值變化越快，這種就一定要加D項
• 下面兩個圖也能看出來誤差變化太快需要D項幫助
  
  這就很明顯了，第一個圖中只有PI作用，那么每當有誤差時，PI的調節就會超調導致誤差更大，越調越超調，離目標值越來越遠，但是加上D項之后就發現會離目標值越來越近，而且微分系數越大阻尼越大，阻尼振蕩越來越小

3.離散PID&程序實現思路

連續和離散形式PID

• 連續PID需要用模擬電路實現，不斷進行計算和調控
• 離散PID則是一個周期進行一次PID計算和調控
• 對離散形式PID的理解:
• 比例項：這里的k表示第k次調控，P項也就是比例系數乘以第k次的調控時刻的誤差
• 積分項：看下面這個圖就是連續和離散化的區別，第一個圖就是積分的定義，其實就是藍色矩形面積之和，T就是寬（T越小求和越準確），error(j)就是長，乘積就是面積，j是一個臨時變量用于使用循環求和
• 微分項：某一點的微分就是斜率，這里也是使用兩點來計算斜率，T也是越小計算結果越精準
  

位置式PID和增量式PID

• 位置式PID能夠應用于各種場景
• 增量式PID其實就是相鄰兩次PID之間的差值
  
• 兩者的區別：位置式可直接給被控對象，增量式需要被控對象有積分功能，也就是需要被控對象擁有記錄上一次狀態的功能，才能在此基礎上根據增量改變
• 兩者直接皆可以實現相互轉化
• 位置式PID輸出的得到的是全量輸出值，如果有噪聲干擾，不同輸出值相差會很大，導致執行機構大幅度變化；增量式PID則可以單獨對輸出值增量進行限幅，防止執行機構大幅度變化
• 增量式PID適合自動控制和手動控制切換的場景，自動控制也就是使用PID，手動控制也就是不使用PID，當你將三個參數全部給0時就是自動控制，這個時候如果是位置式電機會由于參數為0輸出值也立馬變為0，點擊停轉，但是增量式具有存儲上一個輸出量的功能，輸出值可以位置在當前值所以不會停，這個時候就可以手動調節輸出值

PID程序實現

首先確定周期T的值，不能太快也不能太慢，太慢起不到平衡作用，太快硬件傳感器分辨率受限,以下是三種實現每隔時間T實現一次PID調控的方法



第一個方法最簡單但是阻塞式弊端太多；第二個方法定時中斷一般最常用，但是要注意不能在中斷和主函數里操作同一個硬件，避免資源訪問沖突； 第三種也是定時中斷，但是自定義標志位可以在主函數里執行PID調控，該方法主程序一定不能阻塞了

位置式PID程序的實現思路

• 輸出限幅是因為怕PID的輸出值超過了硬件的接受范圍，所以設置一個接受的上下限

增量式PID程序的實現思路

• 這里是控制器內積分得到out而不是out的增量

4.常見優化算法方法

積分限幅（只用于位置式）

• 造成原因：斷電或者電機卡死等原因會使電機的實際速度為0，和目標值相差過大，導致積分項會一直無限制積分，而此時一旦又通電，由于積分項太大了電機會滿速運轉，直到積分項反向積分使電機轉速實際值與目標值重合，此時改變目標值才會有效果，在此之前無論如何修改目標值都沒用。電機通電滿速運轉一段時間且無法控制是危險的
• 實現思路：限制誤差積分的增大上限，也就是哪電機停轉了，也不能讓積分項一直增大，而是增大到一定值就停止增大
• 閾值設置：最大閾值也就是讓積分項=最大輸出值，此時誤差積分=最大out值/K_i
  

積分分離（定位置）

• 常見的都是定速使用PI，定位置用于PD就夠了，當定位置使用PD時會發現實際值與目標值總會有那么一點點誤差無法消除，是因為理論上只要有PWM電機就會動，但是實際上有摩擦力，PWM很小時驅動力只能夠平衡摩擦力，推不動電機旋轉，導致一點點的穩態誤差，我們也知道積分項可以用來消除穩態誤差，實際上確實可以，但是用于定位置控制時又會出現更大的問題——超調，而且這個超調微分項不能解決
• 使用積分項的超調原因：理論上定位置不存在穩態誤差，因為摩擦力基本可以忽略不計，我們只使用比例項完全就夠用了，因為定位置最后OUT輸出值也為0，電機不旋轉，也就是比例項的輸出值剛好就是整個OUT輸出值（OUT_p=OUT），此時加上積分項后，就會是OUT_p+OUT_i>OUT，這就會導致超調，實際圖像就是下圖所示，會先超過目標值，然后此時比例項迅速反應并進行反向積分，積分項會迅速反向積分，當積分項正向積分與反向積分抵消時，此時比例項才會使誤差為0
  
• 解決方法：當誤差大時使用PD，誤差很小時使用PID，防止積分項一直積分導致驅動力不可避免的過大導致超調，如果只在后半段接近目標值才積分，積分時間很短，積分項很小不會產生過大驅動力導致超調
  
• 分離閾值的設置：使用外力施加于電機并觀察波形，使用較大外力時，此時誤差會很大，此時閾值比誤差值大一點就行，太小了會導致當外力迅速變化時積分項迅速為0，導致此時無積分項來抗衡外力；太大了會導致積分項還是太大了導致超調

變速積分

• 變速積分其實就是積分分離的升級版，積分分離是只存在有積分項和無積分項兩種情況，變速積分則是積分項大小會隨誤差大小變化而變化，麻煩的是需要設置一個函數表示變化關系，如果函數不好的話，效果甚至不如積分分離
  
  

微分先行

• 當目標值突然變化時，微分項是誤差的斜率，也就是起初微分項接近正無窮大，后面誤差變化正常，斜率是負的反向微分而且微分項會越來越小
  
• 目標值頻繁切換導致數據產生尖峰，且K_d越大尖峰越高，按理來說只存在微分項時，只改變目標值電機不會旋轉，因為微分項只起到給實際值添加阻尼效果，應該不具備輸出能力，但是實際上純微分項控制時電機會由于誤差快速變化導致旋轉，那么其實可以只對實際值進行微分，無論誤差如何變化，此時微分項就只起到加阻尼效果而不具備輸出能力，而且實際值也不會突變。在計算誤差進行PI之前提前對實際值進行微分，這就是微分先行的原理
• 但是實際情況要看使不使用微分先行，因為微分項可以幫助比例項更快響應目標值變化，尤其是誤差較大的變化，如果只需要微分項起到阻尼效果可以加微分先行
  

不完全微分

• 觀察上面的圖，紅色曲線代表噪聲，綠色曲線是理想值，噪聲對比例項來說影響很小，就是噪聲和理想值的誤差值之差，一般噪聲和理想值不會相差很大；對積分項來說就是曲線下的面積，噪聲有時候比理想值高有時候也有低的時候，所以實際面積兩者相差不大；微分項代表斜率，看圖可知理想值的斜率為正的時候，噪聲可能直接為負值了，這個影響就很大，所以需要過濾噪聲也就是添加濾波器，也就是不完全微分
• 之所以不對開始的值全部濾波，是因為濾波會增加時延，導致PID響應速度變慢
• 不完全微分的微分項就是本次微分項和上次微分項占不同權重然后加起來得到新的微分項，a取0.5相當于均值濾波，a越大本次微分項權重越低，濾波效果就越好
• 一階慣性單元濾波公式：假設輸入是x(k),輸出是y(k),則有y(k)=(1-a)x(k)+ay(k-1),意思是本次輸出為本次輸入和上次輸出的加權平均值
  

輸出偏移

• 也就是PWM要么就不輸出，一旦輸出，該PWM就一定要能驅動電機
• 偏移量需要單獨寫一個測試程序測量
• 缺點就是很難穩定，因為PID但凡調控電機必定轉動，目標值與實際值會一直存在誤差很難為0，甚至目標值都在抖動有噪聲，所以就會一直抖動
  

輸入死區

• 死區閾值
  

注意事項

• 積分限幅一般都要使用
• 微分項可以幫助比例項更快響應目標值變化，尤其是誤差較大的變化，如果只需要微分項起到阻尼效果可以加微分先行
• 輸出偏移+輸入死區可以將誤差控制在可接受范圍，但是積分分離可以無誤差，但是會有積分項的滯后性
• 濾波有延時性，濾波效果越好延時一般越嚴重

5.雙環PID基本原理

串級PID簡介

• 關鍵所在：使用外環PID的輸出值作為內環PID的目標值，但是內外環的PID的實際值都會返還給當前環
• 可以對更多物理量進行控制，性能更好，比如可以實現點擊定速定位控制，也就是讓電機以指定速度來到指定位置停下來

單雙環對比

• 雙環PID相當于單環PID自帶一個定速控制的電機，而且位置環想控制位置時輸出一個值給速度環，當實際位置與目標位置越接近時，位置環輸出越小，速度環目標速度也就越小直到為0，此時電機達到指定位置而且速度也為0
• 不存在啟動力度過小電機轉不起來的問題，因為位置環的目標位置設置很小時輸出值給到了PI控制的速度環，由于是PI控制那么只要有目標速度而且目標位置與實際位置存在誤差電機一定為轉動而且最終會與目標位置重合
• 抵抗外力的作用更強，因為施加外力時，速度環的目標速度應該為0，卻由于外力產生實際速度，有了誤差就會PI調控產生一個阻力對抗外力，而且又存在位置環，施加外力導致位置改變，位置環又要產生負向輸出值給到速度環，讓速度環的誤差變大，速度環的積分項就會更大從而產生更大的對抗力
• 優點也就是響應速度快，穩定性好，準確性高
• 調參順序：先內環后外環
  
• 內環和外環調控周期可以不同，可以設計總PID調控周期，然后在里面分別設置內環外環的調控周期
• 一般外環調控周期大于或等于內環，一是因為外環輸出值刷新很快內環讀取不過來沒什么意義，二是因為內環一般調控反應更快的物理量，頻率更大
• 需要修改內環PID的積分閾值，為外環的目標值的閾值，然后加上InnerTarget=OuterOut
• 修改內環參數時，先要取消外環對內環的控制，也就是注釋這一句InnerTarget=OuterOut
• 修改內環的速度可以修改內環數值的積分限幅幅值

6.調參技巧

• K_p：不斷改變目標值觀察實際值，然后逐步增大K_p直到實際值開始抖動，然后適當減小K_P讓抖動消失，此時K_p就比較適合
• K_i ：看消除穩態誤差的速度不滿不滿意，不滿意就加大K_i但是不能夠出現大幅度超調
• K_d：太大會出現振蕩，調節PD時，可以將P參數給大一點也沒啥，超調可以用D來調節但是不能振蕩，如果振蕩就要調小K_P
• 三個參數的值建議量程顯示大一點，尤其是使用電位器時候由于電位器的抖動，三個參數并不能完全為0，會出現實際值仍然緩慢跟蹤目標值，量程夠大的話能夠看見應該不是0
• 學會取舍，參數越響應快但是抖動振蕩越嚴重，參數小響應慢但是動作平滑

代碼部分

PID.c

#include "stm32f10x.h"                  // Device header
#include "PID.h"void PID_Update(PID_t *p)
{p->Error1 = p->Error0;p->Error0 = p->Target - p->Actual;if (p->Ki != 0){p->ErrorInt += p->Error0;}else{p->ErrorInt = 0;}p->Out = p->Kp * p->Error0+ p->Ki * p->ErrorInt+ p->Kd * (p->Error0 - p->Error1);if (p->Out > p->OutMax) {p->Out = p->OutMax;}if (p->Out < p->OutMin) {p->Out = p->OutMin;}
}

PID.h

#ifndef __PID_H
#define __PID_Htypedef struct {float Target;float Actual;float Out;float Kp;float Ki;float Kd;float Error0;float Error1;float ErrorInt;float OutMax;float OutMin;
} PID_t;void PID_Update(PID_t *p);#endif