這次，我們來講數據結構的排序的直接插入。

一：排序的思想：把待排序的記錄按其關鍵碼值的大小逐個插入到一個已經排好序的有序序列中，直到所有的記錄插入完為止，得到一個新的有序序列

相當于，我們打牌如上圖時，我們一般都會使用直接插入排序的方法。

即：在3和9直接插入，對吧。

同樣，我們這里的直接排序也是按這種方法來思考。

那么，我們先來上它的動圖，來方便我們更清楚。

?

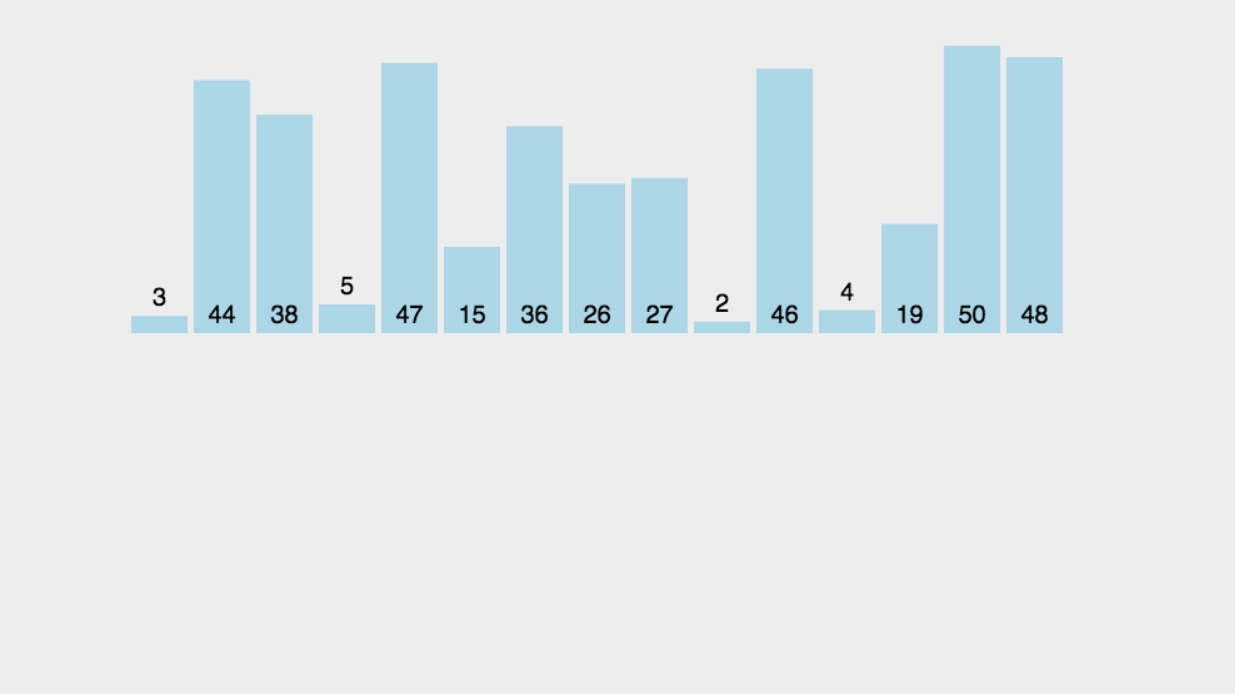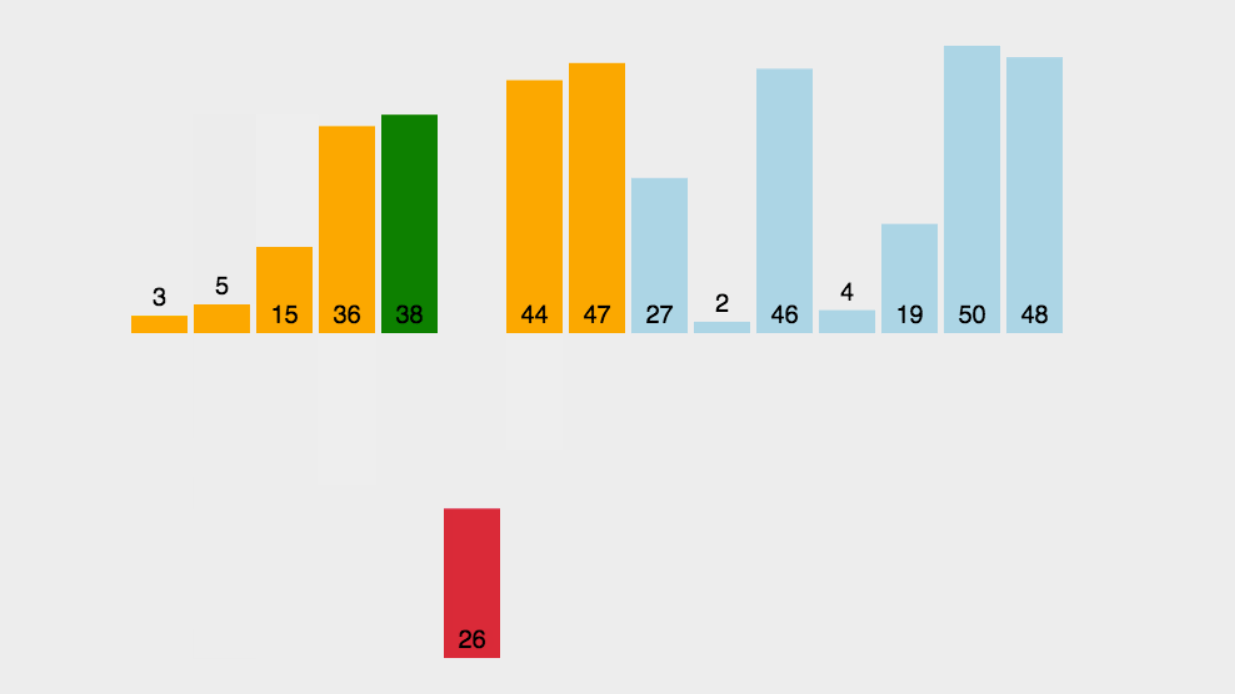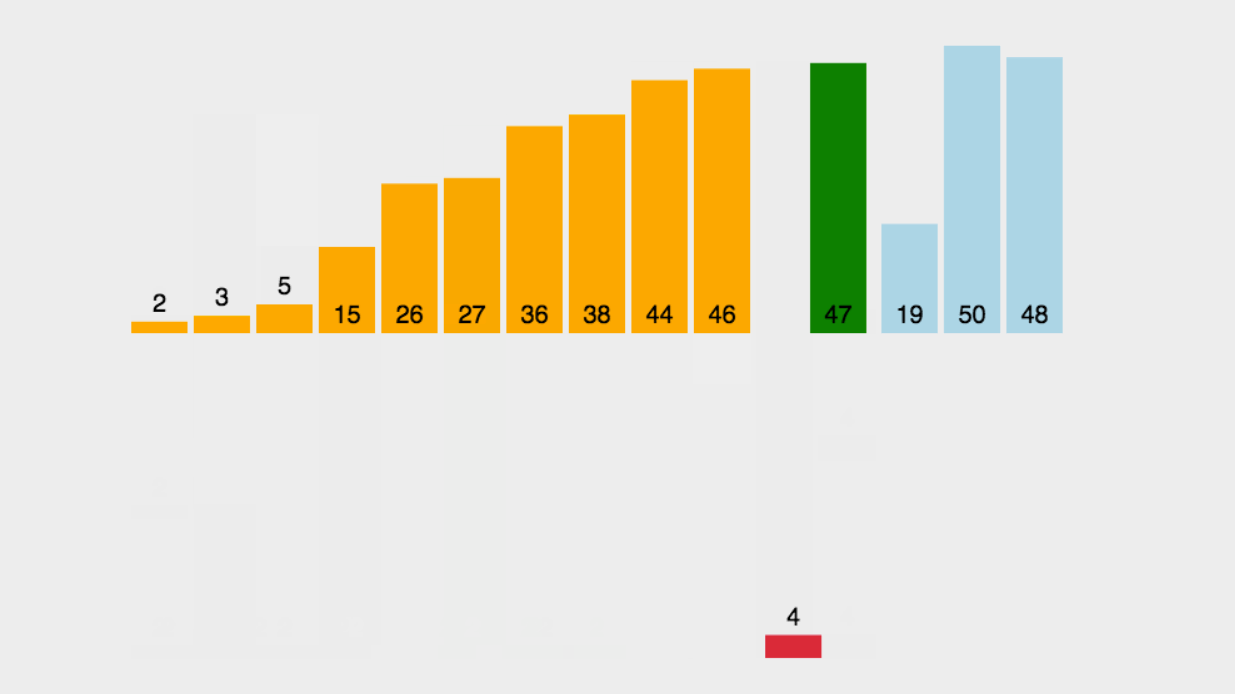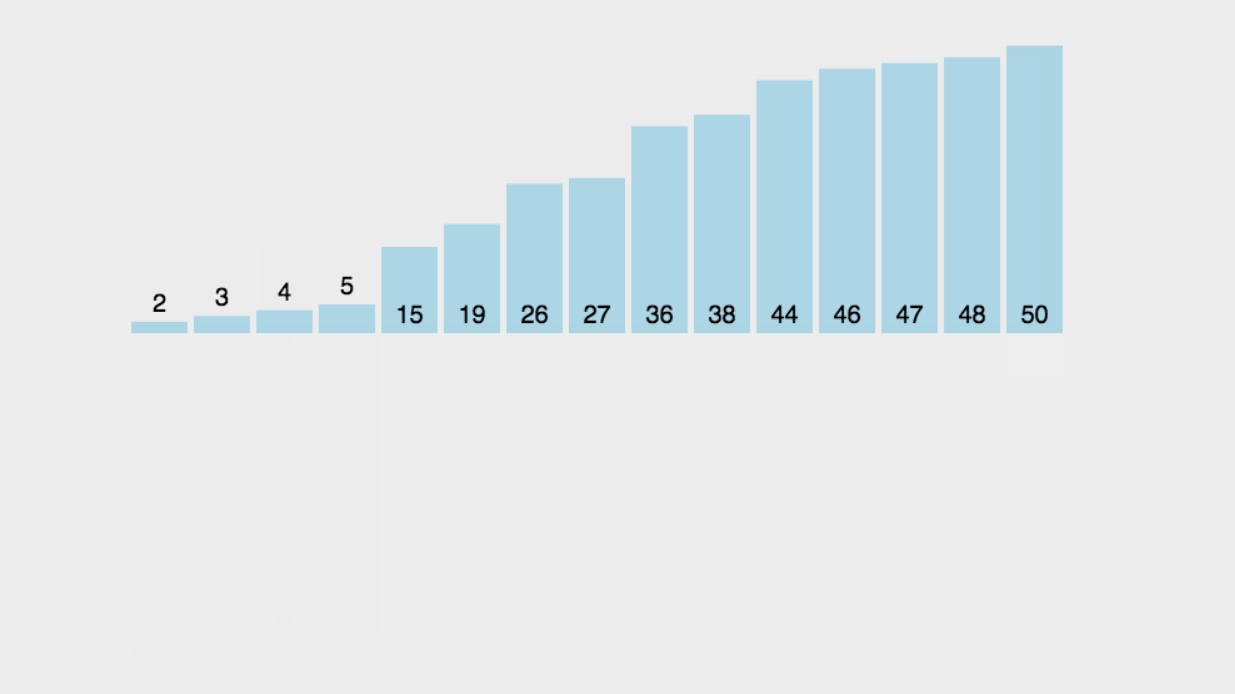
?步驟講解：（升序）

1.一開始的時候，當第一個的時候，它肯定是有序的，所以我們從第二個數開始插入并比較。

2.先把第二個數用臨時變量存起來，再去比較，如果它比前面對比數還要小，就將前面對比數挪到后面，臨時變量再去跟更前面的數依次比較。

3.如果臨時變量大于對比那個數，就插入到對比數的后面。

4.循環（數據向前插入）進去，直到全部的數都插到正確的位置。

void InsertSort(int* a, int n)
{//整個for (int i = 1; i < n; i++){//單一個int end = i - 1;int temp = a[i];while (end >= 0){if (a[end] > temp)   //如果對比數大于存入臨時的，就對比數往后挪{a[end + 1] = a[end];end--;}else   //如果對比數小于存入臨時的，就跳出循環{break;}}a[end + 1] = temp;  //在對比數的后面插入數}}

?

直接插入排序的特性總結：

?

1. 元素集合越接近有序，直接插入排序算法的時間效率越高

就比如是

你每次插入是都比前面那個數大，那么你是不是就不需要挪動數據了，

假設你有n個數據，按照上面的情況，你執行的次數就是n-1,這樣效率是不是就高了。

此時的最好時間復雜度：O(N)。

?

2.

那么最壞的情況呢？

就是逆序。這樣你每次插入的時侯，都是要跟前面的對比數挪動

此時的?時間復雜度：O(N^2)。

?

3. 空間復雜度：O(1)，它是一種穩定的排序算法

?

4. 穩定性：穩定

?

優化排序---希爾排序

上面我們已經知道，插入排序的時間復雜度O(N^2).

那么有什么辦法使他們的效率更高一點呢？

這里大佬們提出了希爾排序的方法。

思路：

1.用間隔為gap的變量分別對每組數插入

2.預排序：它的目標就是接近有序

3.最后再直接插入

這樣的方法會大大提高效率。

比如說，你看：按照下面的話分組

這一趟排序完，是不是就看起來比沒有排時變有序了。?

?

?

?

?

這樣，一趟趟地回來，到gap==1時，就只需挪隔壁的數字比較，所以大大提高了直接插入的效率。

?

比較：

我們知道上面直接排序：

直接插入：完全逆序時：

?它比較執行的次數（1+2+3……n-1）次

根據等差數列的公式：n^2/2-n/2;

那么，我們使用希爾排序，（用gap分組）

gap=gap/4時

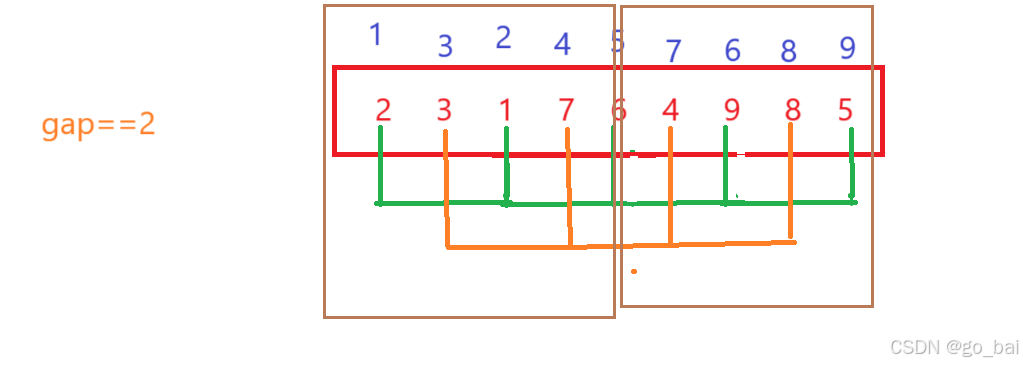
分成兩部分：

那么它的次數（1+2+……+n/2-1）+（1+2+……+n/2-1）

那么計算得到：n^2/4-n/2;

相比，你看，是不是就提高了效率。

?

gap=gap/2

假設為n，則分成3部分

執行的次數：（1+2+3+……n-1）*3

計算得：?n^2/6-n/2;

?

類比得：當我們分的部分越多，執行的次數會減少。

有以下規律：

當分成部分k，執行次數：

1/k*n^2/2-n/2

?

當gap越小，跳得越慢，越有序，當gap越大，跳得越慢，越無序。

那么我們發現，當gap很小時，它的次數本來是n^2/2-n/2，但是，，我們考慮到之前我們已經經過預排序了，已經很接近有序了，所以按照最好的情況來算。

?

總結：

?希爾排序法的基本思想是：先選定一個整數，把待排序文件中所有記錄分成個組，所有距離為的記錄分在同一組內，并對每一組內的記錄進行排序。然后，取，重復上述分組和排序的工作。當到達=1時，所有記錄在統一組內排好序。?

希爾排序的特性總結：

1. 希爾排序是對直接插入排序的優化。

2. 當gap > 1時都是預排序，目的是讓數組更接近于有序。當gap == 1時，數組已經接近有序的了，這樣就會很快。這樣整體而言，可以達到優化的效果。我們實現后可以進行性能測試的對比。

3. 希爾排序的時間復雜度不好計算，因為gap的取值方法很多，導致很難去計算，因此在好些樹中給出的希爾排序的時間復雜度都不固定

根據大佬們的推算，一般都是gap=(gap/3）+1常用

?

?

int gap = n;while (gap > 1){gap = gap / 3 + 1;for (int i = 0; i < gap; i++){for (int i = 0; i < n - gap; i += gap){//單個int end = i;int temp = a[i + gap];while (end >= 0){if (a[end] > temp){a[end + gap] = a[end];end -= gap;}else{break;}}a[end + gap] = temp;}}}}

好了，選擇排序和希爾排序就寫完了。

最后，學路漫漫，永無止境，一點一點進步吧！

?