文章目錄
- 📑前言
- 一、前向傳播與反向傳播
- 1.1 前向傳播(Forward Propagation)
- 1.2 反向傳播(Backpropagation)
- 二、損失函數和優化算法
- 2.1 損失函數(Loss Function)
- 2.2 優化算法(Optimization Algorithms)
- 三、梯度下降法及其變種
- 3.1 梯度下降法(Gradient Descent)
- 3.2 梯度下降法的變種
- 四、小結

📑前言
深度學習是當今人工智能領域的核心技術,尤其在圖像處理、語音識別、自然語言處理等領域表現出色。要理解深度學習,首先需要掌握神經網絡的訓練過程,包括前向傳播、反向傳播、損失函數、優化算法以及梯度下降法及其變種。
一、前向傳播與反向傳播
1.1 前向傳播(Forward Propagation)
前向傳播是神經網絡的計算過程,通過輸入層傳遞到輸出層。每個神經元接收輸入信號,進行加權求和,并通過激活函數得到輸出。這個過程層層遞進,最終在輸出層得到預測結果。以下是一個簡單的前向傳播過程的步驟:
- 輸入層: 輸入數據 x 傳入網絡。
- 隱藏層: 每個隱藏層節點
 接收上一層節點的輸出,并進行加權求和:
接收上一層節點的輸出,并進行加權求和: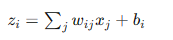 其中
其中 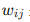 是權重,
是權重,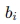 是偏置。
是偏置。 - 激活函數: 通過激活函數
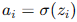 ,將線性組合結果非線性化。
,將線性組合結果非線性化。 - 輸出層: 類似隱藏層的計算方式,最終輸出預測結果。
通過前向傳播,神經網絡可以將輸入映射到輸出,這一過程是通過層層傳遞的方式實現的。
1.2 反向傳播(Backpropagation)
反向傳播是神經網絡訓練的核心算法,用于調整網絡的權重和偏置,以最小化預測結果與真實值之間的誤差。其基本步驟如下:
- 計算損失: 使用損失函數計算預測輸出
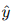 與真實標簽
與真實標簽 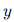 之間的誤差
之間的誤差 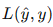 。
。 - 反向傳遞誤差: 從輸出層開始,逐層向后計算每個神經元的誤差,并傳遞到前一層。
- 計算梯度: 對每個權重和偏置,計算損失函數關于它們的梯度

- 更新權重和偏置: 使用梯度下降法或其變種,更新網絡的權重和偏置,使得損失函數值逐步減小。
反向傳播的核心在于鏈式法則,通過逐層計算和傳播梯度,最終調整所有參數,使網絡的預測能力不斷提高。
二、損失函數和優化算法
2.1 損失函數(Loss Function)
損失函數是衡量神經網絡預測值與真實值之間差距的指標。常見的損失函數有:
- 均方誤差(MSE): 主要用于回歸問題,計算預測值與真實值之間的平方誤差平均值。
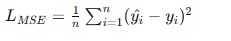
- 交叉熵損失(Cross-Entropy Loss): 主要用于分類問題,衡量預測概率分布與真實分布之間的差異。
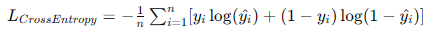
2.2 優化算法(Optimization Algorithms)
優化算法用于調整神經網絡的權重和偏置,以最小化損失函數值。常見的優化算法包括:
- 梯度下降法(Gradient Descent): 通過計算損失函數的梯度,并沿著梯度的反方向更新參數,逐步減小損失函數值。
- 隨機梯度下降(SGD): 每次僅使用一個或小批量樣本來計算梯度并更新參數,適用于大規模數據集。
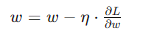
- 動量法(Momentum): 在更新參數時加入前一次更新的動量,幫助加速收斂并減少震蕩。
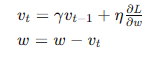
- AdaGrad: 根據梯度歷史動態調整學習率,對稀疏數據表現良好。
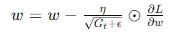
- RMSprop: 結合了動量和AdaGrad的優點,通過指數加權平均平滑梯度平方和。
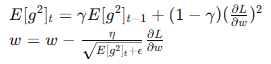
- Adam: 結合動量和RMSprop,適用于各種類型的神經網絡和數據集。
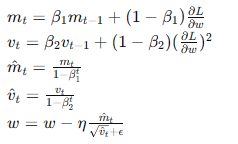
三、梯度下降法及其變種
3.1 梯度下降法(Gradient Descent)
梯度下降法是神經網絡訓練中最基本的優化算法,通過計算損失函數相對于參數的梯度,并沿梯度的反方向更新參數。基本的梯度下降法步驟如下:
- 初始化參數: 隨機初始化網絡的權重和偏置。
- 計算梯度: 使用反向傳播算法,計算損失函數關于每個參數的梯度。
- 更新參數: 根據梯度和學習率,更新網絡的權重和偏置。
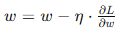
其中,η 為學習率,控制每次更新的步長。
3.2 梯度下降法的變種
為了提高訓練效率和效果,梯度下降法有多種變種,每種變種都有其獨特的特點和應用場景:
- 批量梯度下降(Batch Gradient Descent):
- 使用整個訓練集來計算梯度和更新參數。
- 優點:每次更新都使用了全部數據,梯度計算準確。
- 缺點:計算開銷大,內存占用高,不適用于大規模數據集。
- 隨機梯度下降(Stochastic Gradient Descent, SGD):
- 每次僅使用一個樣本來計算梯度并更新參數。
- 優點:計算速度快,適用于大規模數據集。
- 缺點:梯度更新波動較大,可能導致收斂速度慢。
- 小批量梯度下降(Mini-Batch Gradient Descent):
- 使用一個小批量樣本來計算梯度并更新參數。
- 優點:折中批量梯度下降和隨機梯度下降的優點,計算效率高,收斂較快。
- 缺點:需要選擇合適的批量大小(通常在32到256之間)。
- 動量法(Momentum):
- 在梯度更新中引入動量,幫助加速收斂并減少震蕩。
- 公式:
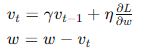
- 優點:在凹谷形狀的損失面中加速收斂,減少震蕩。
- AdaGrad:
- 根據梯度歷史動態調整學習率,對稀疏數據表現良好。
- 公式:
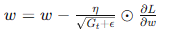
- 優點:在學習率調整上表現出色,適用于稀疏數據集。
- 缺點:學習率可能會過早地變得過小。
- RMSprop:
- 結合了動量和AdaGrad的優點,通過指數加權平均平滑梯度平方和。
- 公式:
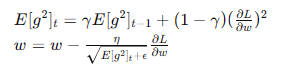
- 優點:在深度學習中表現穩定,適應性好。
- Adam(Adaptive Moment Estimation):
- 結合動量和RMSprop,適用于各種類型的神經網絡和數據集。
- 公式:
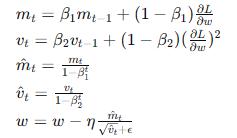
- 優點:廣泛適用,具有良好的收斂性和穩定性。
四、小結
神經網絡的訓練過程是深度學習的核心,前向傳播和反向傳播是其基本步驟,而損失函數和優化算法則決定了模型的性能。梯度下降法及其變種提供了多種優化選擇,使得神經網絡能夠高效地學習和改進。


)


)


)






-2-non-explicit one argument constructor)



