739. 每日溫度

單調棧應該從棧底到棧頂 是遞減的。

找下一個更大的 ，用遞減單調棧，就可以確定在棧里面的每個比當前元素i小的元素，下一個更大的就是這個i，然后彈出并記錄；然后當前元素i入棧，仍然滿足遞減要求。最后留在棧里面的是沒有下一個更大的值的，符合要求。

找下一個更小的用遞增單調棧同理。

result[被彈出下標]=使他彈出下標-被彈出下標。

復習一下Java集合知識：來自Java集合詳解-CSDN博客

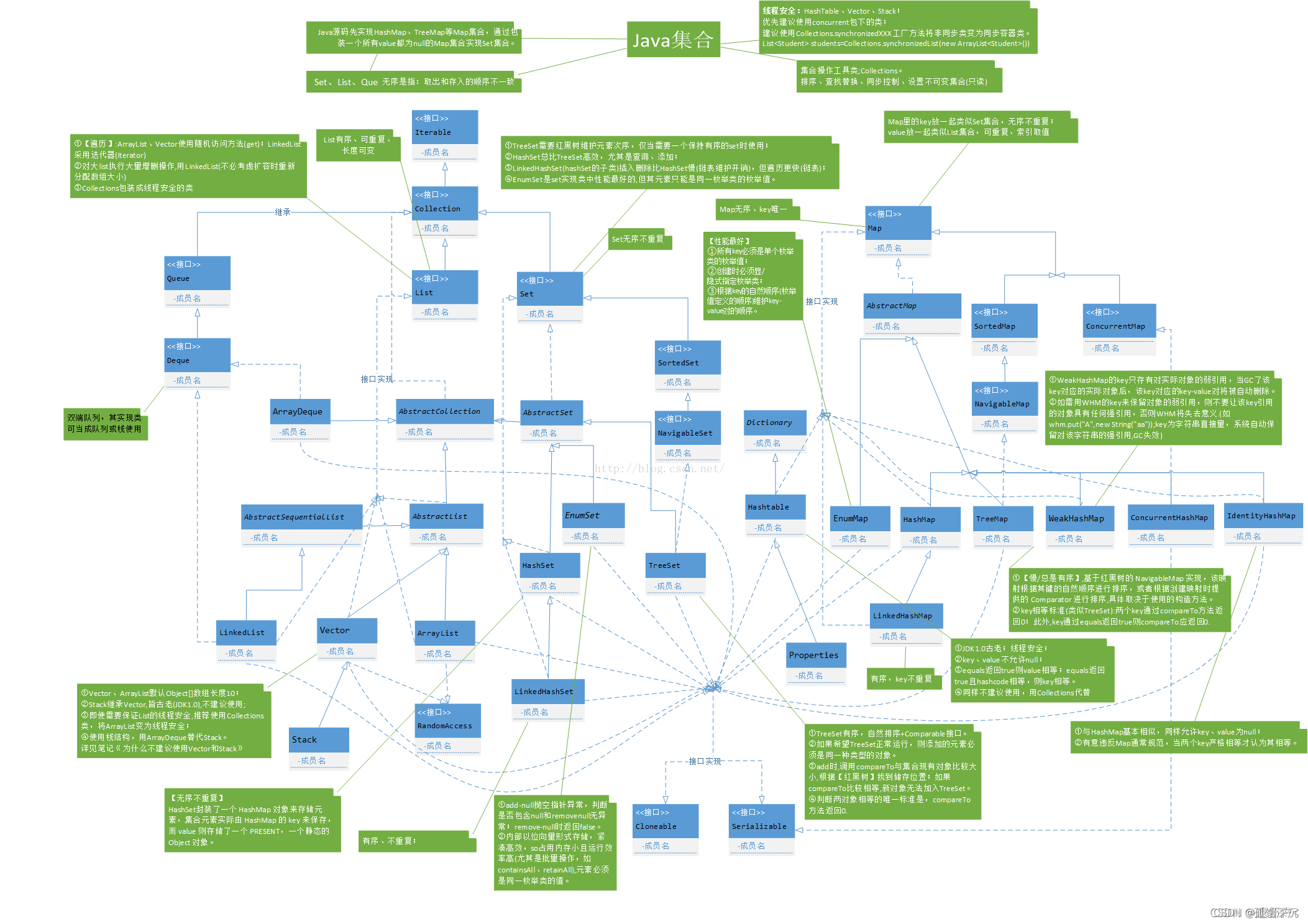
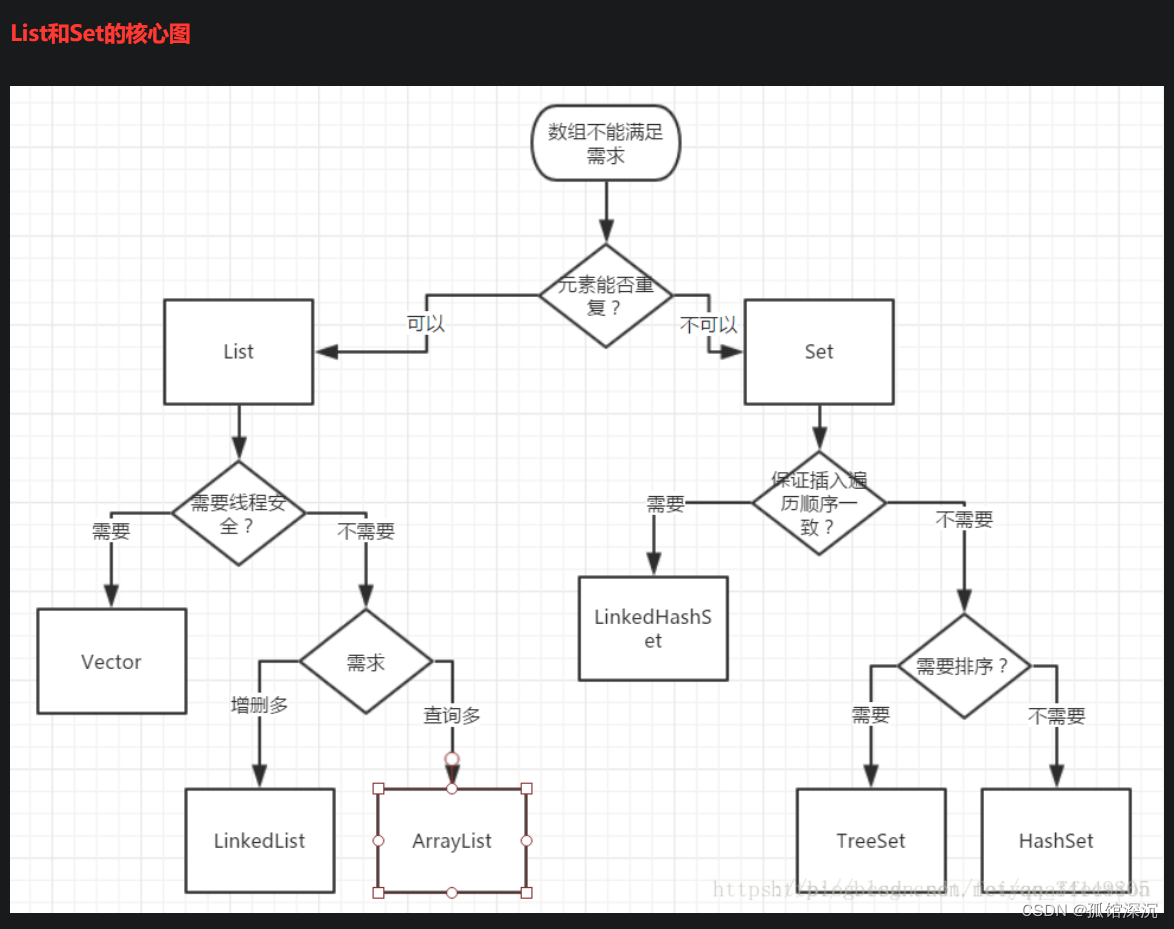
LinkedList 可以使用多種接口進行聲明，包括但不限于：

• Deque 接口：Deque<Integer> deque = new LinkedList<>();: 雙端隊列的操作，包括棧和隊列的功能。
• Queue 接口：Queue<Integer> queue = new LinkedList<>();: 適合實現隊列的操作，包括 offer、poll、peek 等方法。
• List 接口：List<Integer> list = new LinkedList<>();: 通用的集合操作，如添加、刪除、獲取元素等。
• Collection 接口：Collection<Integer> collection = new LinkedList<>();: 這種聲明方式表示通用的集合操作，適合需要簡單地操作元素集合的場景。

class Solution {public int[] dailyTemperatures(int[] temperatures) {int n=temperatures.length;Deque<Integer> stack=new LinkedList<>();//放下標，int [] result =new int[n];for(int i=0;i<n;++i){int temp=temperatures[i];while(!stack.isEmpty() && temperatures[stack.peek()]<temp){int a=stack.pop();//小，被彈出result[a]=i-a;}//找到位置stack.push(i);}return result;}
}

時間、空間O(n)

496. 下一個更大元素 I

跟上一題區別是，先用單調棧把nums2處理，較小的元素彈出來的時候要找到當前元素i在nums1的位置，然后給到result。

這里不算下標而且數組里面沒有重復元素，所以單調棧里面可以放元素值。

另外result一開始都賦值-1。最后可能nums1里有幾個是沒有下一個更大值的。

class Solution {public int[] nextGreaterElement(int[] nums1, int[] nums2) {int m=nums1.length ,n=nums2.length ;Deque<Integer> stack=new LinkedList<Integer>();int[] result=new int[m];HashMap<Integer,Integer> hash=new HashMap<>();// 放元素for(int i=0;i<m;++i){hash.put(nums1[i],i);}for(int i=0;i<m ;++i){result[i]=-1;}for(int i=0;i<n;++i){int tmp=nums2[i];while(!stack.isEmpty() && stack.peek()<tmp){int a=stack.pop();//被彈出的元素aint pos=hash.getOrDefault(a,-1);if(pos!=-1)result[pos]=tmp;}stack.push(tmp);}return result;}
}

時間是O(m+n)。初始化result和hash的是O(m)，單調棧循環是O(n)，因為用的HashMap，查找O(1)。

503. 下一個更大元素 II

要求循環地搜索元素的下一個更大的數，其實就是單調棧要走兩次nums數組。

class Solution {public int[] nextGreaterElements(int[] nums) {int n=nums.length;int[] result=new int[n];Deque<Integer> stack=new LinkedList<>();Arrays.fill(result,-1);for(int j=0;j<2*n;++j){int i=j%n;int num=nums[i];while(!stack.isEmpty() && nums[stack.peek()]<num){int a=stack.pop();result[a]=nums[i];}stack.push(i);}return result;}
}

42. 接雨水

1、以列為單位，每列都找自己左邊（包含自己）的最高柱子 l 和自己右邊（包含自己）的最高柱子 r，就形成一個凹槽。然后每一列應該裝下的雨水數就應該是（min(l , r) - 自己柱子高）*寬。所以主要關注l 和 r 怎么計算。

1.1、DP

維護一個lefts和rights數組，lefts[i]是l，rights[i]就是r。

那么遞推公式就是：（min(lefts[i] , rights[i]) - 自己柱子高）*寬

關鍵得到這兩個數組，還是很直觀的，lefts涉及到的是i及左邊的，所以從左往右遞推；rights從右往左。

class Solution {public int trap(int[] height) {int n=height.length;int count=0;int[] lefts=new int[n];int[] rights=new int[n];lefts[0]=height[0];for(int i=1;i<n;++i){lefts[i]=Math.max(lefts[i-1],height[i]);}rights[n-1]=height[n-1];for(int i=n-2;i>=0;--i){rights[i]=Math.max(rights[i+1],height[i]);}for(int i=0;i<n;++i){count+=(Math.min(lefts[i],rights[i])-height[i]);}return count;}
}

時間空間：O（n）

1.2、雙指針

用兩個指針left、right從兩端，逐漸逼近，逼近的判斷條件是：left指向的和right指向的對比，哪一方小，就走一步。

①這里對于紅框的判斷不能理解，為什么當前的哪一方小，就能確定這一方的最大值更小呢？

下面這個說法很形象。其實就是A隊B隊比賽，遍歷過了的都是輸了的（或者平局的），假如B隊的curB贏了A隊的curA，所以目前MAX_B（其實就是curB）是目前兩隊最強。即A隊最強的其實是輸給B隊過的了，所以A隊最強不如B隊最強。可以確定MAX_B=curB>MAX_A。A贏B就同理。

②又想：假如B隊贏了A隊，可以確定出現了一個凹槽：A隊最高、curA、B隊最高。這個凹槽的兩端一定是我們要求的嗎？

A隊最高肯定是所要求的左邊最高柱子l ，B隊最高不一定是右邊最高柱子 r。假如curA和curB之間還有比MAX_A更矮的柱子，壓根不考慮因為我們是先找兩端最高的，再在兩個最高的里找最小的；假如有比MAX_B更高的柱子，那取Min值仍然還是MAX_A。A贏B就同理。

總的來說，哪一方輸了，哪一方的輸家就可以確定他的雨水了。決定這個雨水高度的就是他這一方的最強者（但是比另一方的最強者弱）。

可以用MAX_B>MAX_A，用height[a]<height[b]感覺更能體現這個“比賽”的過程吧，當前選手的大小。

class Solution {public int trap(int[] height) {int n=height.length;int a=0,b=n-1;//對手int MAX_A=0,MAX_B=0;//一個隊里面已比對手的最強者int count=0;while(a<b){//更新最強者，要包括當前選手MAX_A=Math.max(MAX_A,height[a]);MAX_B=Math.max(MAX_B,height[b]);int yushui=0;//輸的一方收集雨水if(height[a]<height[b])//b整體贏了{yushui=MAX_A-height[a];//注意凹槽兩端a++;//輸的下場，派下一個}else if(height[a]>=height[b]){yushui=MAX_B-height[b];b--;        }count+=yushui;}return count;}
}

時間O(n)空間O(1)

2、以行為單位

2.1 單調棧

以列為單位求，每個柱子的雨水是一次性求好，需要提前知道左邊最高柱子和右邊最高柱子，這形成凹槽1；

以行為單位求，是求以每個柱子為底的這一行能接的雨水，這一行雨水可以到的高度，應該是最接近自己的柱子的最小高度。即Min（上一個更大，下一個更大）。這是凹槽2。

這是按行求 和 按列求 的主要區別。

這一行，寬是 下一個更大和上一個更大的 下標間隔。高是Min值和中間 a 的差。

class Solution {public int trap(int[] height) {int n=height.length;int count=0;Deque<Integer> stack=new LinkedList<Integer> ();for(int i=0;i<n;++i){int tmp=height[i];while(!stack.isEmpty() && height[stack.peek()]<tmp)//凹槽{int a=stack.pop();//l=棧底，a，r=height[i]if(!stack.isEmpty()){int l=stack.peek();int r=i;int kuan=r-l-1;int gao=Math.min(height[l],height[r])-height[a];count+=kuan*gao;}}stack.push(i);}return count;}
}

84. 柱狀圖中最大的矩形

貌似只能以行為單位，所以只看單調棧方法。

需要找到元素i的上一個更小的元素leftmin和下一個更小的元素rightmin，這樣leftmin和rightmin之間的元素都比當前元素i更大，那么矩形的寬就是中間的這些元素：可以從leftmin+1延伸到rightmin-1，長即為height[i]。

怎么確定矩形的寬 和高？寬有左邊界和右邊界，這里感覺應該每次固定一邊然后討論另一邊。這里固定右邊界，是遍歷的i，也就是對于每個柱子i 都計算，以這個元素為右邊界 ，矩形的最大面積。知道右邊界了，要讓面積最大左邊界應該是多少呢？其實應該找上一個更小值l 。這樣 (l,i) 之間都是比i 高或者相等的柱子，這就是固定i 為右邊界的最大面積。

怎么保證能處理所有元素？使用單調棧，pop一個元素就算這個元素右邊界的矩形。題目說柱子都是>=0的，那么在最后的時候 ，單調棧再插入一個0，就能把棧里面的所有元素都pop出來，就都處理到了

單調棧 的順序 應該是 需要 嚴格單調遞增的。因為棧不為空要找上一個更小值l 。之前的題事實上只在單個>、<的時候要出棧，因為只需要求下一個更大/更小。上面的接雨水也是棧頂=當前的話沒關系，相減是0 沒影響。但是這里得嚴格遞增。

過程是：當 i 元素 <= 棧頂的 a，這個時候這個i 元素就是右邊界，我們要討論單調棧里面所有比這個元素大的元素為高的矩形面積。現在 兩種情況：

1、棧頂a彈出，棧為空了，說明什么？在heights里面，a的左邊沒有比他嚴格小于的l ，都是>=他的，而a 的下一個更小值又是i，所以區間是[0,i-1)所以寬就是i；

2、如果棧不為空，那就是存在l ，這個l 就是a彈出之后的新棧頂（比a 要小的）。所以矩形區間是(新棧頂=l，i)。

class Solution {public int largestRectangleArea(int[] heights) {int n = heights.length;Deque<Integer> stack = new LinkedList<>(); // 存儲柱子的索引int maxArea = 0;for (int i = 0; i <= n; ++i) {int h = (i == n) ? 0 : heights[i]; // 最后加入一個高度為0的柱子，確保處理完所有柱子while (!stack.isEmpty() && heights[stack.peek()] >= h) {int a=stack.pop();int height = heights[a]; // 當前出棧的柱子高度// 計算寬度:是i代表前面i個都是>=height的。否則矩形寬是(上一個更小的,i-1]int width = stack.isEmpty() ? i : i - stack.peek() - 1; maxArea = Math.max(maxArea, height * width);System.out.println(maxArea);}stack.push(i); // 當前柱子的索引入棧}return maxArea;}
}

主要是 ：確定一邊求另一邊的思想、求上一個更小值用單調棧、為了處理所有元素添加一個最小值0。