RoPE 旋轉位置編碼，詳細解釋（下）NLP 面試的女生徹底說明白了

原創?看圖學?看圖學?2024年07月01日 07:55?北京

書接上文，上文見：這么解釋 RoPE 旋轉位置編碼，女朋友睜大了雙眼（上）

下面簡單回顧一下上文的重點，后面復數域的解釋會用到一些結論，詳細的可以點擊上面的文章觀看。

實數域的 RoPE 解釋（重點回顧）

RoPE 的實現和解釋，完全可以只在實數域中進行。比如 llama 的實現，就完全沒有用到復數的概念。

而在實數域上關于 RoPE 的解釋，核心就一句話：在內積空間中，內積具有旋轉不變性?。

也就是下面這個性質：

也就是說 兩個旋轉向量的內積等于其中一個向量旋轉它們角度差的結果與另一個原始向量的內積。也可以看作是一個向量逆時針旋轉了?,?另一個向量逆時針旋轉了?，然后這兩個向量又同時順時針旋轉了?,?于是第一個向量處在?的位置，第二個向量則轉到了實數軸上，角度為0. 因為內積的旋轉不變性，兩個內積依然相等。記住這句話，后面在復數域證明還能用。

復數域的 RoPE 解釋

其實涉及到旋轉的計算，到復數域里會變得特別方便，因為虛數? i 的物理含義就是旋轉。

為了理解虛數/復數，我們先拿負數來做個對比。

負數的出現讓人們困惑了很久，我現在有1個蘋果，被女朋友拿走了2個，實在是有些腦殼疼。但是現在我們很容易能理解負數，就是欠我一個蘋果唄。如果較真的話，那 -1 個蘋果在哪里？可能是我從室友那里借了一個。

可以想象一下，在一維的實數軸上，取負可以讓1變成-1，再取負又變成1，然后循環。

還有其他的方法能從1到-1么？這時候認知就要提高了，就好像古代人的活動范圍很小，那自然認為地球是平的。知道后來可以航海，發現為什么船接近的時候為什么總是先看到船帆然后才看到船的身子，這個時候就開始思考了，地球有沒有可能是圓的。

從1到-1如果只在實數軸上移動，那只能是取負。如果把數軸擴展到2維，新增一個虛數軸，那就可以旋轉了。1 乘以 i 就跑到虛數軸的上面，再乘以 i 就跑到-1 了。再乘以i就跑到虛數軸的下面，再乘以i就回到了1. 如下圖所示：

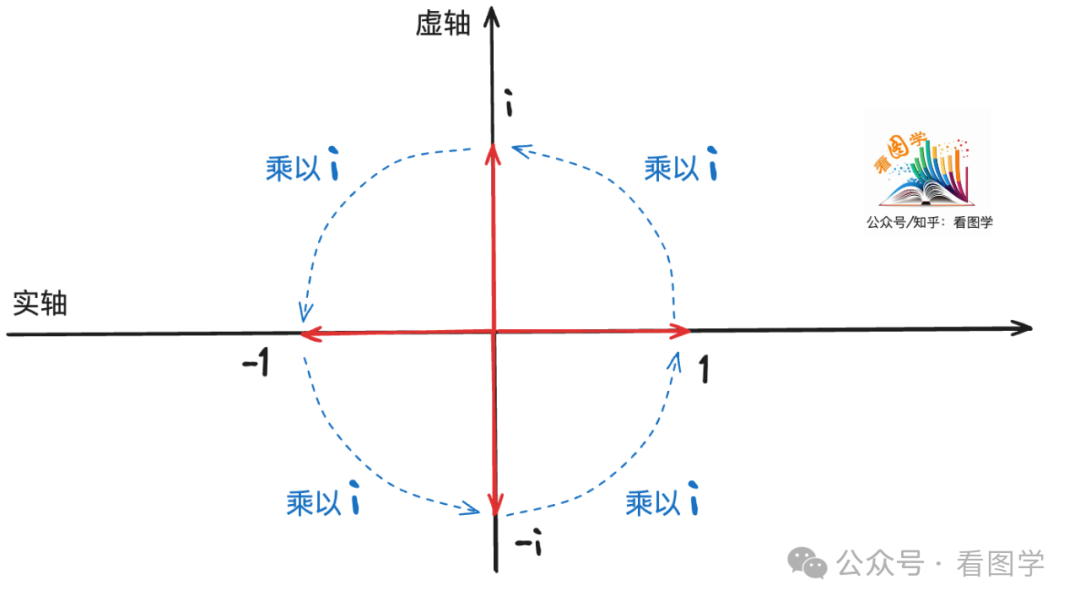
所以為什么?, 其含義就是在復平面上轉了2次，從 1 轉到了 -1.

歐拉公式??提出來很久之后，大家才嘗試從幾何的角度去理解歐拉公式。

歐拉公式其實就是在復平面上旋轉，復平面是一個2d 平面。為了看的更清楚一點呢，我們再升一維。新增一個與復平面正交的軸代表 x。如下面視頻所示。

看圖學

，贊16

這個3維空間上就很好的展示了隨著 x 的增大，?就一直在旋轉的畫圈。這個旋轉的曲線投影到復平面上，那就是在復平面畫圓；如果投影到?x?與 實數軸的平面上，就是?cos?函數；如果投影到 x 與 虛數軸的平面上，那就是?sin?函數。

再回想一下 RoPE 的旋轉角度的函數，恰好就是一個 sin 函數和一個 cos 函數，所以說?RoPE 就如同上面歐拉公式的視頻一樣，在一直轉圈，所以叫旋轉編碼。

然后在實數域證明中，我們已經證明了通過旋轉矩陣來解釋 RoPE。在復數域一個向量旋轉怎么表示呢？非常簡單，逆時針旋轉??度等于 乘以?. 證明如下：

你看，旋轉矩陣又出來了。

所以論文中的

就是 q 和 k 分別旋轉了??和?。

復數域中同樣滿足內積旋轉不變性。只不過復數域中的內積不再是簡單的相乘，而是要取共軛。

比如復數??和?，內積定義為：

其中??是??的共軛復數（論文中的共軛是用??來表示的）。

計算復內積：

之所以采用共軛復數，完全是為了滿足內積的三個性質：正定性，共軛對稱性，第一變元線性。

而共軛復數的物理意義就是順時針旋轉。還記得 逆時針旋轉??度等于 乘以?，那么乘以共軛復數??就是 順時針旋轉??度(?逆時針旋轉 -?度)。

復數域的旋轉不變性證明如下：

這基本上就是 RoPE 在數學上的解釋。

最后論文中就還剩下一個 Re (實部)沒有解釋。看上面復數的內積公式就可以看出，復數域內積的實部(Re)等于實數域兩個向量的內積。也就是

注意左邊二維向量的實數域的表示，右邊則是復數域的表示。

然后 RoPE 的論文里公式的表示似乎沒那么嚴謹，在論文表述的過程中相同的符號含義發生了變化。所以有時候看上去有些困惑，看完本文和下圖的解釋應該就明白了。

?

— END?—

推薦閱讀：

這么解釋 RoPE 旋轉位置編碼，女朋友睜大了雙眼（上）

Transformers 中的 Position Embedding 的作用

看圖學大模型：Transformers 的前生今世(上）

內積，點積，數量積是一樣的么？