題目

證明

的MAP估計量為

其中是一個的矢量, 是一個可逆的p*p的矩陣。也就是說，MAP估計量對可逆的線性變換是可以變換的。

---

解答

已知的聯合概率密度

且：

現在知道：

那么為了獲得變換后的MAP，首先需要根據求出

根據概率密度變換的基本知識：

（具體可以參考：隨機過程——隨機變量的函數變換(換元)_連續型分布函數的變換-CSDN博客）

又因為是可逆的，可以得到：

因此：

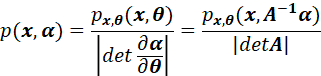
注意，上式本質上是雅可比行列式變換。由于不包含。因此，如果尋找不同下的最大值，等同于尋找不同下的最大值。而又根據的最大值出現在處，那么根據線性關系，就可以得到此時的就是達到最大值對應的，即：

最后，再利用兩個估計量的線性關系，得到：

也就是MAP估計量（此例中的）對可逆的線性變換（此例中的）,直接可以得到變換后新參數的MAP估計量（此例中的）

注意MMSE估計量也有一樣的線性性質，參見書（11.5）公式