B樹的概念及其特點

B樹是一顆多叉的平衡搜索樹，廣泛應用于數據庫和 文件系統中，以保持數據有序并允許高效的插入、刪除和查找操作。下面介紹B樹的特點：

• 多路平衡樹：多路平衡樹其實就是多叉平衡樹，每個節點都有多個指向孩子節點的指針以及鍵值。通常，一顆m階的B樹有k個子節點，有k-1個關鍵字，而k的取值范圍為[ceil(m/2),m]（celi表示向上取整）。例如一顆3階的B樹，最多有3個孩子2個關鍵字。
• 鍵值有序：每個節點中包含多個關鍵字，這些關鍵字是有序的。節點中每個關鍵字都將子節點切割成兩部分，左邊部分的節點的所有關鍵字的值一定是小于該關鍵字的，右邊節點的所有關鍵字的值都是大于該關鍵字的，這一點跟二叉搜索樹的性質相同。
• 樹的高度平衡：所有葉子節點的深度都是一樣的，站在AVL樹的角度講，每個節點的平衡因子都是0。具體如何維護這個平衡性下面會詳細介紹。
• 高效的磁盤讀寫：B樹被設計用于在磁盤上高效的存儲和讀取數據。通過每個節點都有多個鍵值和多個字節的指針，從而減少磁盤的讀寫次數。

下面給出一個3階B樹的節點示意圖：

在設計B樹節點時，孩子數量通常要多一個，這是為了方便后續實現插入操作和刪除操作。概念上我們依舊認為m階B樹的節點的孩子個數為k個，實現的時候認為是k+1個。
我們將一個節點的所有鍵值集合稱為數據域

解析B樹的基本操作

插入數據

為了保證插入節點之后B樹保持其平衡性，我們采用分裂節點來保持樹的結構。具體的插入步驟如下：

1. 查找插入位置：首先從根節點開始，找到應該插入新鍵值的葉子節點。（B樹每一次插入新鍵值都一定在葉子節點處）
2. 插入鍵值：在找到的葉子節點處插入新鍵值。如果該葉子節點的鍵值已經滿了，即關鍵字的個數等于m+1，則需要對該葉子節點進行分裂。分裂的操作步驟如下：
   • 找到節點數據域的中間位置
   • 給一個新節點，將中間位置右邊的所有數據（包括鍵值和孩子指針）搬到新節點中。新節點是被分裂節點的兄弟節點。
   • 將中間位置的鍵值移動放到父親節點中，如果沒有父節點，那就再創建一個父節點，并連接。

插入數據模擬

現在假設我們有一顆階數為3的B樹（每個節點最多有3個孩子和2個鍵值），并按以下順序插入鍵值：10, 20, 5, 6, 12, 30, 7, 17。

• 當插入了10、20之后：
  
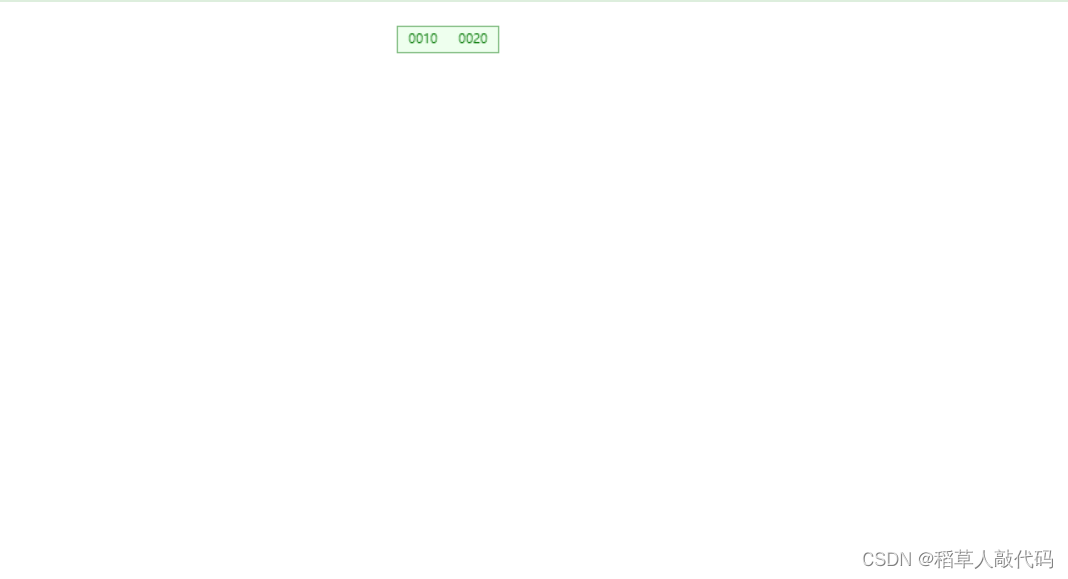
  只有一個節點，該節點已經有兩個鍵值分別是10、20，現在這個節點的鍵值已經滿了。
• 插入5，節點鍵值溢出需要分裂：
  
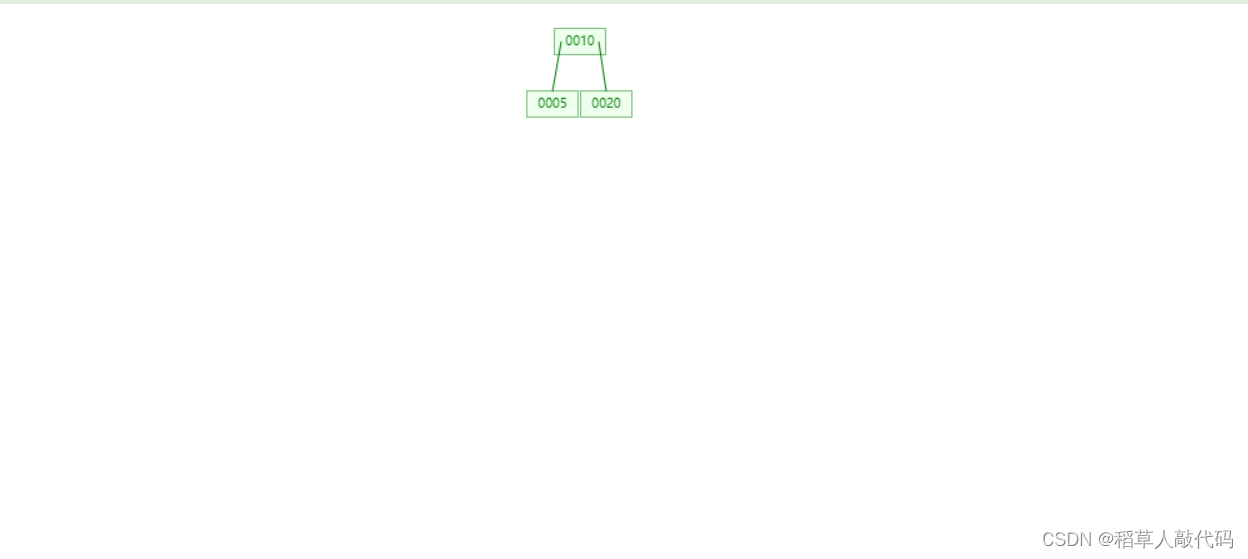
  仔細觀察上述結果，根據插入數據的步驟，插入節點的鍵值滿了，需要分裂。找到數據域的中間位置，也就是10的位置，10右邊的數據全部移動到新兄弟節點中，再把中間鍵值10提取出來插入到父親節點中。由于沒有父節點，則新創建一個父節點。

點擊觀看分裂演示過程
點擊觀看整個插入過程

分析分裂如何維護平衡性

為什么分裂操作會保證B-樹維持特性呢？以下是具體分析：

• 保證葉子節點在同一深度：分裂只是在滿節點的基礎上進行的，將中間鍵提升到父節點并不會改變葉子節點的深度差，如果父節點滿了，那父節點再分裂。如果父節點不存在，那么就會創建一個新父節點，此時這個新父節點一定成為了B樹的根節點，也就意味著每條葉子節點分支的高度都會+1。
• 控制節點的鍵值數量：每次分裂出去的鍵值數量都是大約一半，新的兄弟節點擁有的鍵值數量和被分裂節點的鍵值數量幾乎一致。這樣就保證了B樹每個節點的鍵值數目在[ceil(m/2)?1,m?1]之間。
• 分裂后有序：由于中間鍵值的選擇，新的兄弟節點的所有鍵值一定都大于被分裂節點剩下的鍵值。再將中間鍵值插入到父節點中，中間鍵的左孩子指向被分裂節點，右孩子指向新兄弟節點，這樣一來，整顆樹還是一顆搜索樹。

分析B樹的性能

設n為B樹的總鍵值數量，m為B樹的階數。則每個節點最多有m個孩子節點，m-1個關鍵字。

• 查找效率：查找操作在B樹中的時間復雜度為O(log n)，原因如下：

  • B樹的高度h和節點的最小度數t以及總鍵值數n的關系為：h=logt(n),因為每個節點至少有t個子節點。
  • 在每個節點中查找特定鍵值的時間復雜度為O(t),但由于t是一個常數，所以總時間復雜度就是O(1)。（t是B樹的最小度數ceil(m/2),是確定的）
  • 查找的總時間效率就是樹的高度乘每個節點查找特定鍵值的時間，也就是O(log n)

• 插入操作：插入操作的時間復雜度也是O(log n)，具體分析如下

  • 查找到插入位置的時間復雜度為O(logn)
  • 插入后可能需要分裂節點，分裂操作的時間復雜度為O(t),這是因為每個節點最多包含t個鍵值。
  • 由于樹的高度較小且分裂操作是局部的，整體插入操作的時間復雜度仍為O(log n)。

• 刪除操作：刪除操作的時間復雜度也是O(log n),具體分析：

  • 查找到目標節點的時間復雜度為O(log n)
  • 刪除操作可能涉及節點的合并或鍵值的重新分配，這些操作的時間復雜度都是O(t),同樣由于t是常數，總體的時間復雜度還是O(log n)

綜上，B樹各種操作時間效率都是logn。下面分析B樹的空間復雜度：
B樹的空間復雜度主要受到節點數目的影響。每個節點包含k-1個鍵值和k+1個子節點指針，節點總數與樹的高度和階數有關。由于B樹是多路平衡樹，其空間復雜度可以表示為O(n),其中n是鍵值總數。

B+樹和B*樹

B+樹

B+樹是B樹的變形，在B樹的基礎上優化的多路平衡樹，B+樹的規則和B樹類似，但在B樹的基礎上做了以下幾點改進優化：

• 分支節點的子節點指針數量和關鍵字的個數相同（或者是子節點數量比關鍵字個數多1）
• 分支節點不存儲實際的數據，只用于引導查找路徑（存儲的是孩子節點的最小關鍵字）
• 所有的實際數據都存在葉子節點中
• 葉子節點按照鍵值排序，彼此之間用一個指針連接，形成一個鏈表

下面給出一顆B+樹結構示意圖：

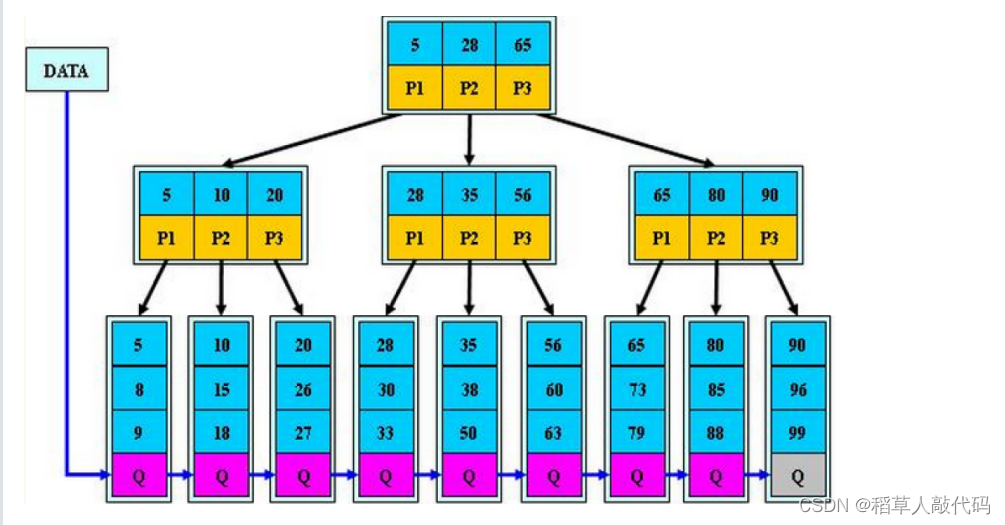
在B+樹中如何查找一個數據呢？步驟如下：

和B樹一致，從根節點開始逐層向下查找，比較當前鍵值和目標鍵值，如果大于目標鍵值，說明當前鍵值的孩子分支的所有值都大于目標鍵值。所以我們需要找到一個第一個大于目標鍵值的前一個鍵值種去尋找。點擊演示B+樹插入數據的動畫。

B+樹的分裂

當一個結點滿時，分配一個新的結點，并將原結點中1/2的數據復制到新結點，最后在父結點中增加新結點的指針；B+樹的分裂只影響原結點和父結點，而不會影響兄弟結點，所以它不需要指向兄弟的指針。

時間復雜度和空間復雜度和B數一樣。

B+樹的優勢

• 范圍查詢非常高效，因為葉子節點通過鏈表連接，可以順序訪問所有滿足范圍條件的節點。范圍查詢性能優于B樹。
• 插入和刪除操作相對簡單一些，因為數據只存儲在葉子節點中，只需在葉子節點中維護平衡
• B+樹適用于高效訪問和順序訪問的場景

B*

B*樹是B+樹的變形，在B+樹的非根和非葉子節點再增加指向兄弟節點的指針。具體結構如下：

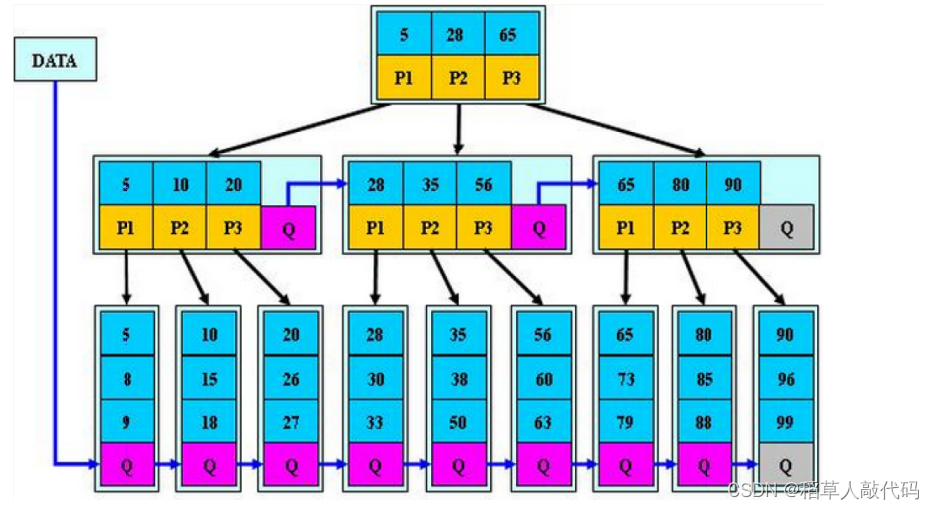
B*樹的分裂

當一個結點滿時，如果它的下一個兄弟結點未滿，那么將一部分數據移到兄弟結點中，再在原結點插入關鍵字，最后修改父結點中兄弟結點的關鍵字（因為兄弟結點的關鍵字范圍改變了）；如果兄弟也滿了，則在原結點與兄弟結點之間增加新結點，并各復制1/3的數據到新結點，最后在父結點增加新結點的指針。所以，B*樹分配新結點的概率比B+樹要低，空間使用率更高；

總結

• B樹：有序數組+平衡多叉樹
• B+樹：有序數組鏈表+平衡多叉樹
• B*樹：一棵更豐滿的，空間利用率更高的B+樹