原題鏈接🔗：二叉搜索樹中第K小的元素
難度：中等????

題目

給定一個二叉搜索樹的根節點 root ，和一個整數 k ，請你設計一個算法查找其中第 k 小的元素（從1開始計數）。

示例 1：

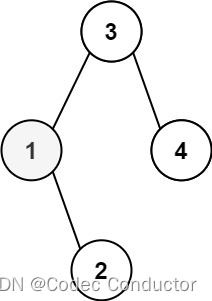
輸入：root = [3,1,4,null,2], k = 1
輸出：1

示例 2：

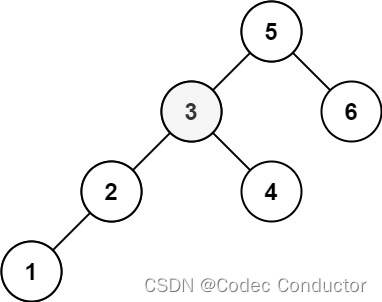
輸入：root = [5,3,6,2,4,null,null,1], k = 3
輸出：3

提示：

• 樹中的節點數為 n 。
• 1 <= k <= n <= 10⁴
• 0 <= Node.val <= 10⁴

進階：如果二叉搜索樹經常被修改（插入/刪除操作）并且你需要頻繁地查找第 k 小的值，你將如何優化算法？

題解

二叉搜索樹

二叉搜索樹（Binary Search Tree，簡稱BST）是一種特殊的二叉樹，它具有以下性質：

1. 有序性：對于樹中的每個節點，其左子樹上所有節點的值都小于該節點的值，其右子樹上所有節點的值都大于或等于該節點的值。

2. 沒有兄弟節點：每個節點最多只有一個左子節點和一個右子節點。

3. 每個節點存儲一個鍵值：在二叉搜索樹中，每個節點通常存儲一個鍵值，該鍵值用于維護樹的有序性。

4. 樹結構：二叉搜索樹是樹結構，這意味著它是一個沒有環的分層數據結構。

5. 平衡性：理想情況下，二叉搜索樹是平衡的，即左右子樹的高度差不超過1。平衡的二叉搜索樹可以保證操作（如搜索、插入和刪除）的時間復雜度為O(log n)。但在最壞的情況下，如果插入的元素是有序的，樹將退化成鏈表，時間復雜度變為O(n)。

二叉搜索樹的應用非常廣泛，因為它提供了高效的數據存儲和檢索方式。以下是一些基本操作：

• 搜索：在BST中搜索一個元素，可以從頭節點開始，根據目標值與當前節點值的比較結果，決定是向左子樹還是向右子樹搜索。這個過程可以遞歸或迭代進行，直到找到目標值或到達葉子節點。

• 插入：向BST中插入一個新元素，首先搜索該元素應該插入的位置，然后根據BST的性質將其插入到適當的位置。

• 刪除：從BST中刪除一個元素，需要考慮幾種情況：刪除的節點沒有子節點、有一個子節點或有兩個子節點。在刪除節點后，需要調整樹以保持BST的性質。

• 遍歷：BST可以通過前序、中序、后序和層序遍歷來訪問所有節點。中序遍歷特別有用，因為它將按照升序訪問所有節點。

二叉搜索樹的實現通常涉及到遞歸和迭代技術，以及對樹結構的深入理解。在實際應用中，為了提高性能，可能會使用自平衡的二叉搜索樹，如AVL樹或紅黑樹。

中序遍歷

二叉樹的中序遍歷是一種遍歷二叉樹的方法，其遍歷順序為：先遍歷左子樹，然后訪問根節點，最后遍歷右子樹。這種遍歷方式可以確保在訪問任何節點之前，其所有左子節點已經被訪問過，同樣地，在訪問任何節點之后，其所有右子節點也會被訪問。

中序遍歷對于二叉搜索樹（BST）特別有用，因為它會按照節點值的非遞減順序訪問所有節點，即中序遍歷的結果是一個有序數組。

以下是中序遍歷的基本步驟：

1. 訪問左子樹：首先，遞歸地對左子樹進行中序遍歷。

2. 訪問根節點：然后，訪問根節點。在遍歷過程中，通常會將根節點的值添加到一個列表中。

3. 訪問右子樹：最后，遞歸地對右子樹進行中序遍歷。

中序遍歷的時間復雜度為O(n)，其中n是樹中節點的數量，因為它需要訪問樹中的每個節點。空間復雜度取決于遞歸調用的深度，最壞情況下是O(n)（當樹退化成鏈表時），最好情況下是O(log
n)（當樹是平衡的）。

中序遍歷遞歸法

1. 解題思路：

在LeetCode上，題目“二叉搜索樹中第K小的元素”通常要求你找到一個二叉搜索樹（BST）中第K小的元素。二叉搜索樹的性質是：對于樹中的任何節點，其左子樹上的所有節點的值都小于該節點的值，其右子樹上的所有節點的值都大于該節點的值。

解題思路如下：

• 理解BST的性質：首先，要利用BST的性質來簡化問題。在BST中，中序遍歷（左-根-右）會以遞增的順序訪問所有節點。

• 中序遍歷：由于題目要求找到第K小的元素，我們可以通過中序遍歷BST來實現。在遍歷過程中，記錄訪問的節點數量。

• 計數與停止：在中序遍歷的過程中，當訪問到第K個節點時，停止遍歷。這個節點就是所求的第K小的元素。

• 遞歸或迭代：中序遍歷可以通過遞歸或迭代的方式實現。遞歸是更直觀的方法，但迭代可以避免潛在的遞歸深度問題。

• 實現算法：編寫代碼實現上述邏輯。

2. c++ demo：

#include <iostream>
#include <vector>// 定義二叉樹的節點結構
struct TreeNode {int val;TreeNode* left;TreeNode* right;TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
};class Solution {
public:// 主函數，接收二叉搜索樹的根節點和K值，返回第K小的元素int kthSmallest(TreeNode* root, int k) {std::vector<int> elements;inOrderTraversal(root, elements, k);return elements[k - 1]; // 由于數組索引從0開始，所以用k-1}private:// 中序遍歷輔助函數，同時接收一個vector來存儲遍歷結果void inOrderTraversal(TreeNode* node, std::vector<int>& elements, int k) {if (!node || elements.size() >= k) {return;}// 遍歷左子樹inOrderTraversal(node->left, elements, k);// 訪問當前節點if (elements.size() < k) {elements.push_back(node->val);}// 遍歷右子樹inOrderTraversal(node->right, elements, k);}
};// 示例使用
int main() {// 構建一個示例二叉搜索樹//       3//      / \//     1   4//      \//       2TreeNode* root = new TreeNode(3);root->left = new TreeNode(1);root->right = new TreeNode(4);root->left->right = new TreeNode(2);Solution solution;int k = 3; // 假設我們要找第3小的元素std::cout << "The " << k << "st smallest element is: " << solution.kthSmallest(root, k) << std::endl;// 清理分配的內存（在實際應用中應該使用智能指針來自動管理內存）delete root->left->right;delete root->left;delete root->right;delete root;return 0;
}

• 輸出結果：

The 3st smallest element is: 3

3. 代碼倉庫地址：kthSmallest