文章目錄
- 視頻教程
- 第一章 計算機圖形學概述
- 計算機圖形學的定義
- 計算機圖形學的應用
- 計算機圖形學 vs 圖像處理 vs模式識別
- 圖形顯示器的發展及工作原理
- 理解三維渲染管線
- 第二章 基本圖元的掃描轉換
- 掃描轉換
- 直線的掃描轉換
- DDA算法
- Bresenham算法
- 中點畫線算法
- 圓的掃描轉換
- 中點畫圓算法
- 反走樣
- 第三章 多邊形填充
- 概念
- 有效邊表的填充思路
- 有效邊表的算法實現
- 邊緣填充
- 種子填充算法
視頻教程
孔令德 | 計算機圖形學網上課堂:30個知識點的微課講解
第一章 計算機圖形學概述
計算機圖形學的定義
定義:計算機圖形學是一門研究怎樣用計算機表示、生成、處理和顯示圖形的學科。
分類:
- 幾何圖形:基于線框模型 描述
- 真實感圖形:基于表面模型 描述

圖形表示方法:
- 參數法
- 點陣法
計算機圖形學就是研究 將圖形的表示法從參數法轉換到點陣法 的一門學科。
圖形學之父:Ivan E. Sutherland
單選:計算機圖形學與計算機圖象學的關系是(B)
A.計算機圖形學是基礎,計算機圖象學是其發展
B.不同的學科,研究對象和數學基礎都不同,但它們之間也有可轉換部分
C.同一學科在不同場合的不同稱呼而已
D.完全不同的學科,兩者毫不相干
計算機圖形學的應用
| 應用領域 | 內容 |
|---|---|
| 計算機游戲 | 計算機游戲的核心技術來自于計算機圖形學,如多分辨率地形生成、天空盒紋理、角色動畫、碰撞檢測、粒子系統、自然景物模擬、交互技術、實時繪制等。計算機游戲是計算機圖形學發展的一個重要推動力。 |
| 計算機輔助設計 | 計算機輔助設計(Computer Aided Design,CAD)和計算機輔助制造(Computer Aided Manufacture,CAM)是計算機圖形學最早應用的領域,也是當前計算機圖形學最成熟的應用領域,典型的代表產品為AutoCAD系統軟件。現在建筑、機械、飛機、汽車、輪船、電子器件等產品的開發幾乎都使用AutoCAD進行設計。Autodesk公司出版的另外兩個三維建模、動畫和渲染軟件是3ds max和Maya,前者主要用于建筑物建模,后者主要用于角色建模。 |
| 計算機藝術 | 計算機圖形學廣泛應用于美術設計中,稱為計算機藝術。動畫設計是其典型代表。動畫是計算機藝術的典型代表。根據人眼的視覺暫留特性,將一系列的單幅靜態畫面(frame,幀)串接在一起,以24-30幀/秒的速度播放,形成運動的效果。 |
| 虛擬現實 | 虛擬現實(virtual reality,VR)技術是利用計算機生成虛擬環境,逼真地模擬人在自然環境中的視覺、聽覺、運動等行為的人機交互的新技術。借助于一些特殊設備,如數據手套、頭盔顯示器等,用戶可以“沉浸”到該環境中。在虛擬現實中,感受到的是虛擬環境設備反饋的作用力,從而產生身臨其境的感覺。 |
| 計算機輔助教學 | 計算機輔助教學是利用計算機圖形學技術展示抽象原理或不可見過程的一種新的教學方法。在多媒體教室,教師使用集圖、文、聲、像為一體的多媒體課件進行教學,有助于學生理解和接受深奧枯燥的理論。 |
單選:下面哪一項不屬于計算機圖形學的應用范圍?(B)
A.計算機動畫
B.從遙感圖像中識別道路等線劃數據
C.三維可視化技術
D.影視三維動畫制作
判斷題:分形技術在自然景物的模擬中發揮了重要作用。(正確)
判斷題:虛擬現實技術屬于計算機圖形學的應用范圍。(正確)
簡答題:請簡述計算機圖形學的應用領域有哪些?請列舉三個以上的應用領域。
答:
計算機圖形學已經在游戲、電影、科學、藝術、商業、廣告、教學、培訓和軍事等領域獲得了廣泛的應用。
應用領域包括但不限于:
- 計算機游戲
- 計算機動畫
- 計算機輔助設計與輔助制造
- 計算機輔助教學
- 虛擬現實
計算機圖形學 vs 圖像處理 vs模式識別
- 計算機圖形學:從抽象數據到圖像的過程,主要用于圖像的生成和渲染。
- 圖像處理:是在圖像已經存在的基礎上,通過算法對其進行加工和改善,改進圖像質量或提取信息。
- 模式識別:從圖像出發,試圖理解圖像內容并將其轉換為抽象的描述,是一種從圖像到數據的過程。
計算機圖形學的研究內容不包括:圖像處理和模式識別
圖形顯示器的發展及工作原理
判斷題:CRT由四部分組成:電子槍、聚焦系統、偏轉系統和熒光屏。(正確)
- 光柵掃描顯示器:畫點設備,即點陣單元發生器,并可控制每個點陣單元的亮度,這些點陣單元被稱為像素。
- 幀緩沖存儲器(顯存):幀緩沖中單元數目與顯示器上的像素數目相同,而且單元與像素一一對應。要在屏幕上顯示圖像,首先要把圖像信息寫入幀緩沖,然后光柵掃描顯示器訪問幀緩沖,再把其中的內容顯示到屏幕上。
備注:幀緩沖單元的數值決定了顯示器像素的顏色。顯示器顏色的種類與幀緩沖中每個單元的位數有關。
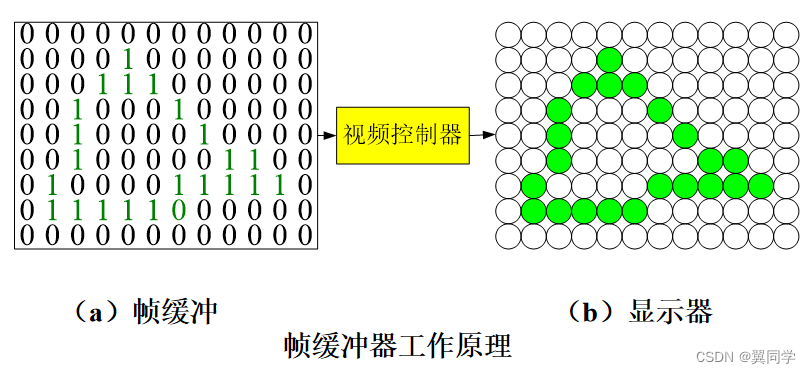
- 1 個位面:每個像素的顏色只用一位(Bit)表示(其值非0即1),此時屏幕只能顯示黑白二色圖像,稱為黑白顯示器
- 8個位面:每個像素的顏色用一個字節(Byte)表示,幀緩沖器需要用八個位面,可表示 2 8 2^{8} 28 種灰度,稱為灰度顯示器。
- 24個位面:每個像素用R、G、B三原色混合表示,其中每種原色分別用一個字節表示,各對應一把電子槍,每種顏色可有256種亮度,三種顏色的組合是 2 24 2^{24} 224 顏色。
問題:對于分辨率為1024*1024的光柵系統,若每一像素用8位和12位二進制來表示存儲信息,各需多大光柵存儲容量以及顯存?每一屏幕最多能顯示多少顏色?若R,G,B灰度都占8位,其顯示顏色的總數是多少?
答:
8位表示:
- 每個像素用8位(1字節)來表示。
- 分辨率為1024*1024,即總共有1024 * 1024 = 1,048,576個像素。
- 因此,總存儲容量為1,048,576字節(即1,048,576 * 8位 = 8,388,608位)。
- 在8位表示下,每一屏幕最多能顯示的顏色數為 2 8 = 256 2^8 = 256 28=256種顏色。
12位表示:
- 每個像素用12位來表示。
- 分辨率為1024*1024,即總共有1024 * 1024 = 1,048,576個像素。
- 總存儲容量為1,048,576 * 12位 = 12,582,912位,轉換為字節為12,582,912 / 8 = 1,572,864字節。
- 在12位表示下,每一屏幕最多能顯示的顏色數為 2 12 = 4096 2^{12} = 4096 212=4096種顏色。
R,G,B各占8位時的顏色總數:
- R、G、B每種顏色有256種亮度(即 2 8 2^8 28種)。
- 三種顏色組合的總顏色數為 2 8 ? 2 8 ? 2 8 = 2 24 = 16 , 777 , 216 2^8 * 2^8 * 2^8 = 2^{24} = 16,777,216 28?28?28=224=16,777,216種顏色。
單選題:分辨率為 1024×1024 的顯示器,需要多少位面數為8的幀緩存(A)
A.1M
B. 2M
C. 3M
D.4M
解析:
- 分辨率為1024×1024的顯示器意味著總共有1024 * 1024 = 1,048,576個像素點。
- 如果每個像素點需要8位(即1字節)來表示其顏色信息,那么總共需要的字節數為1,048,576字節。
- 由于1M(兆)字節等于1,048,576字節,因此需要的幀緩存大小為1M字節。
單位換算:
- 1字節 = 8位
- 1兆字節(MB)= 1,048,576字節 = 2 20 2^{20} 220字節
單選題:分辨率為1024×1024的顯示器各需要多少位面數為16的幀緩存(B)
A.1M
B. 2M
C. 3M
D.512K
解析:
- 分辨率為1024×1024的顯示器意味著總共有1024 * 1024 = 1,048,576個像素點。
- 如果每個像素點需要16位來表示其顏色信息,那么總共需要的位數為1,048,576像素 * 16位/像素 = 16,777,216位。
- 將位數轉換為字節數(因為1字節 = 8位),所需的字節數為16,777,216位 / 8 = 2,097,152字節。
- 由于1M字節等于1,048,576字節,所以2,097,152字節等于2M字節。因此,需要的幀緩存大小為2M字節。
理解三維渲染管線
三維渲染管線:將三維場景轉化為二維圖像的過程,涉及以下階段:
-
應用程序階段:
- 任務:處理場景中的對象,包括它們的幾何形狀、位置、動畫、物理效果等。
- 輸出:將場景中需要渲染的幾何體(圖元)及其屬性(如攝像機位置、光照條件)輸出到下一個階段。
-
幾何階段:
- 模型視點變換:將模型從局部坐標系轉換到世界坐標系,再從世界坐標系轉換到觀察者(攝像機)坐標系。
- 頂點著色:計算頂點的光照效果,為后續的光柵化階段提供必要的顏色信息。
- 投影:將三維場景投射到二維視平面上,涉及透視投影或正交投影。
- 裁剪:移除那些完全不在視野內的圖元,減少后續階段的計算量。
- 屏幕映射:將裁剪后的圖元映射到屏幕坐標系,為光柵化階段準備。
-
光柵化階段:
- 任務:將幾何階段處理后的圖元轉換為屏幕上的像素點,涉及插值計算(如深度、顏色、紋理坐標等)。
- 輸出:最終渲染的二維圖像,包括確定哪些像素屬于哪個圖元,以及這些像素的具體顏色和屬性。
選擇題:三維渲染管線實現計算機內一個三維模型從數據到圖像的轉換過程。該過程包括下面的步驟,請按渲染管線的流程,選擇合適的處理步驟填入空(1)~ 空(6)
三維模型加載??空(1)??空(2) ?? 空(3)?? 空(4)??空(5)?? 空(6)??顯示在顯示器上
- A. 觀察變換
- B. 模型變換(三維幾何變換)
- C. 投影變換
- D. 消隱
- E. 光柵化(掃描轉換)
- F. 計算頂點光照(顏色)
答案:B A C D F E
過取樣:在高于顯示分辨率的較高分辨率下用點取樣方法計算,然后對幾個像素的屬性進行平均得到較低分辨率下的像素屬性。實際上是把顯示器看成是比實際更細的網格來增加取樣率。
單選題:在Windows中,繪圖一般在視圖窗口的客戶區進行,使用的是MFC的設備上下文類( B )中的各種繪圖函數。
A.MFC
B. CDC
C. DEC
D. PDC
單選題:MFC中的繪圖一般在視圖類的(屏幕/打印機)繪圖消息響應函數( D )中進行。
A.paint
B. main
C. OnPaint
D.OnDraw
簡答題:請簡述三維渲染管線的處理流程。
答:
三維渲染管線,用于將三維場景轉換為二維圖像,主要有以下處理流程:
-
應用程序階段:處理場景中的各種對象,包括它們的幾何形狀、位置、動畫和物理效果等,最終輸出場景中需要渲染的幾何體(圖元)及其相關屬性,如攝像機位置和光照條件。
-
幾何階段:模型視點變換,將模型從局部坐標系轉換到世界坐標系,然后轉換到觀察者(攝像機)坐標系。接著進行頂點著色,計算頂點的光照效果。之后是投影,將三維場景投射到二維視平面上,裁剪步驟移除那些完全不在視野內的圖元,最后屏幕映射將裁剪后的圖元映射到屏幕坐標系,為光柵化階段做準備。
-
光柵化階段:將幾何階段處理后的圖元轉換為屏幕上的像素點,涉及到插值計算,如深度、顏色、紋理坐標等。最終輸出是渲染的二維圖像,
第二章 基本圖元的掃描轉換
掃描轉換
- 概念:確定最佳逼近圖形的像素集合,并用指定屬性寫像素的過程稱為圖形的掃描轉換,也稱為光柵化。
- 作用:將矢量圖形轉換為像素陣列,以在光柵圖形顯示器上顯示。
單選題:多邊形掃描轉換可以將( A )。
A.多邊形由頂點表示轉換成點陣表示
B. 多邊形由區域表示轉換成邊界表示
C.多邊形轉換為顯示器的掃描線
D.多邊形的填充屬性改變
簡答題:請簡述什么是掃描轉換?
答:
確定最佳逼近圖形的像素集合,并用指定屬性寫像素的過程稱為圖形的掃描轉換或光柵化。
直線的掃描轉換
定義:在幀緩沖器有限的像素中,尋找一組能最接近真實直線的像素點,對這些像素進行寫操作。
直線的斜截式方程如下:
y = k x + b y = kx + b y=kx+b
其中:
- k k k —— 直線的斜率
- b b b —— 直線在 y y y軸的截距
給定兩點 ( x 1 , y 1 ) (x_1, y_1) (x1?,y1?)和 ( x 2 , y 2 ) (x_2, y_2) (x2?,y2?),則直線的斜率 k = y 2 ? y 1 x 2 ? x 1 k = \frac{y_2 - y_1}{x_2 - x_1} k=x2??x1?y2??y1??,其中主位移 Δ \Delta Δ 定義為:
Δ = max ? ( Δ x , Δ y ) \Delta = \max(\Delta x, \Delta y) Δ=max(Δx,Δy)
在直線掃描轉換過程中,根據主位移方向執行加 1 1 1或者減 1 1 1操作,以確定直線上的像素點。
DDA算法
已知過端點 ( x 1 , y 1 ) (x1, y1) (x1,y1), ( x 2 , y 2 ) (x2, y2) (x2,y2) 的直線段 y = k x + b y=kx+b y=kx+b,斜率 k k k 為 y 2 ? y 1 x 2 ? x 1 \frac{y_2 - y_1}{x_2 - x_1} x2??x1?y2??y1??。
DDA算法:
- 當 ∣ k ∣ ≤ 1 |k| \le 1 ∣k∣≤1:當 x x x每遞增 1 1 1, y y y 遞增 k k k (即直線斜率)
- 當 ∣ k ∣ > 1 |k| > 1 ∣k∣>1:當 y y y每遞增 1 1 1, x x x 遞增 k k k (即直線斜率)
大題:請用DDA直線掃描轉換算法,計算(0,0)(6,4)直線上的點,將下面的表格填寫完整:
| x | y |
|---|---|
| 0 | 0 |
| 【】 | 【】 |
| 【】 | 【】 |
| 【】 | 【】 |
| 【】 | 【】 |
| 【】 | 【】 |
| 6 | 4 |
答:
對于直線(0,0)到(6,4),我們首先計算斜率 k k k:
- k = y 2 ? y 1 x 2 ? x 1 = 4 ? 0 6 ? 0 = 2 3 k = \frac{y_2 - y_1}{x_2 - x_1} = \frac{4 - 0}{6 - 0} = \frac{2}{3} k=x2??x1?y2??y1??=6?04?0?=32?
由于 ∣ k ∣ ≤ 1 |k| \le 1 ∣k∣≤1,我們將從 ( x 1 , y 1 ) = ( 0 , 0 ) (x1, y1) = (0, 0) (x1,y1)=(0,0) 開始,每次 x x x 遞增 1 1 1, y y y 遞增 k k k,直到 x = x 2 x = x2 x=x2。
計算過程中, y y y 的值需要四舍五入到最近的整數。
| x | y |
|---|---|
| 0 | 0 |
| 1 | 1 |
| 2 | 1 |
| 3 | 2 |
| 4 | 3 |
| 5 | 3 |
| 6 | 4 |
解釋:
- 從 ( 0 , 0 ) (0, 0) (0,0) 開始。
- 每次 x x x 遞增 1 1 1, y y y 遞增 k = 2 3 k = \frac{2}{3} k=32?。
- y y y 的值在每一步都四舍五入到最近的整數。
單選題:直線DDA算法,當斜率m<1時,x方向的增量△x和y方向的增量△y分別是?( C )
A. ±m 和 ±1
B. ±1 和 ±1/m
C. ±1 和 ±m
D. ±1/m 和 ±1
判斷題:在DDA算法中,當斜率大于1時,則y方向為主步進方向。(正確)
Bresenham算法
Bresenham 算法的基本思想:主位移方向每次遞增一個像素,另一個方向的增量是 0 0 0 或 1 1 1 ,取決于像素點與理想直線的距離。這個距離稱之為誤差項,用 d d d 表示。
以 x x x 主位移方向為例, x i + 1 = x i + 1 x_{i+1} = x_i + 1 xi+1?=xi?+1,則:
y i + 1 = { y i + 1 , ( d ≥ 0.5 ) y i , ( d < 0.5 ) y_{i+1} = \begin{cases} y_i + 1, ~~ (d \ge 0.5) \\ y_i, ~~ (d < 0.5) \end{cases} yi+1?={yi?+1,??(d≥0.5)yi?,??(d<0.5)?
令 e i + 1 = d i + 1 ? 0.5 e_{i+1} = d_{i+1} - 0.5 ei+1?=di+1??0.5,則:
y i + 1 = { y i + 1 , ( e ≥ 0 ) y i , ( e < 0 ) y_{i+1} = \begin{cases} y_i + 1, ~~ (e \ge 0) \\ y_i, ~~ (e < 0) \end{cases} yi+1?={yi?+1,??(e≥0)yi?,??(e<0)?
單選題:Bresenham直線掃描轉換法中,從理想直線到位于直線上方的像素的距離為t,到位于直線下方的像素的距離為s,s-t>=0的時候,選擇如下哪個點?(A)
A.直線上方的點
B. 直線下方的點
C.理想直線上的點
D.不確定
整數化的 bresenham 算法描述如下:
int e = -dx;
for(i = 0; i <= dx; i++) {drawpixel(x, y, color);x++;e += 2 * dy;if(e >= 0) {y++;e -= 2 * dx;}
}
也就是說, e e e 初始化為 ? Δ x - \Delta x ?Δx,然后循環 Δ x \Delta x Δx 次,其中每次:
- x x x 都是加 1 1 1, e e e 加 2 Δ y 2\Delta y 2Δy
- 一旦 e ≥ 0 e \ge 0 e≥0 了, y y y 就可以加 1 1 1,然后將 e e e 減掉 2 Δ x 2 \Delta x 2Δx。
單選題:使用 Bresenham 直線掃描轉換法,繪制直線段 P 0 ( 0 , 0 ) P_0(0,0) P0?(0,0) —— P 1 ( 5 , 2 ) P_1(5,2) P1?(5,2),在 x = 3 x=3 x=3 時, y y y 應該是?(A)
A.1
B. 0
c. 2
D. 3
解析:
根據上面【整數化的 bresenham 算法代碼描述】,我們將數值代入,很容易計算出答案。

首先,我們需要確定 Δ x \Delta x Δx 和 Δ y \Delta y Δy 的值。對于直線段 P 0 ( 0 , 0 ) P_0(0,0) P0?(0,0) 到 P 1 ( 5 , 2 ) P_1(5,2) P1?(5,2):
- Δ x = 5 ? 0 = 5 \Delta x = 5 - 0 = 5 Δx=5?0=5
- Δ y = 2 ? 0 = 2 \Delta y = 2 - 0 = 2 Δy=2?0=2
此時 x x x 為主位移方向,根據 bresenham 算法, e e e 初始化為 ? Δ x = ? 5 - \Delta x = -5 ?Δx=?5。然后,我們將按照算法步驟進行迭代:
| x x x | y y y | e e e 初始值 | e e e 加 2 Δ y 2\Delta y 2Δy 后 | 條件 e ≥ 0 e \ge 0 e≥0 是否成立? | 如果 e ≥ 0 e \ge 0 e≥0,請給出 e e e 減 2 Δ x 2\Delta x 2Δx 后的結果 |
|---|---|---|---|---|---|
| 0 | 0 | ? 5 -5 ?5 | ? 1 -1 ?1 | 否 | |
| 1 | 0 | ? 1 -1 ?1 | 3 3 3 | 是 | ? 7 -7 ?7 |
| 2 | 1 | ? 7 -7 ?7 | ? 3 -3 ?3 | 否 | |
| 3 | 1 | ? 3 -3 ?3 | 1 1 1 | 是 | ? 9 -9 ?9 |
因此,在 x = 3 x = 3 x=3 時, y y y 應該是 1 1 1。
中點畫線算法
中點算法原理: x x x 方向上每次加 1 1 1 , y y y 方向上加不加 1 1 1 取決于中點誤差項的值。
整數化的中點畫線算法流程如下:
public void drawLine(int x0, int y0, int x1, int y1) {int dx = x1 - x0;int dy = y1 - y0;int d = dx - 2 * dy; // 關鍵int x = x0;int y = y0;while (x <= x1) {// 繪制點(x, y)plot(x, y);if (d > 0) { d -= 2 * dy;x++;} else {d += 2 * (dx - dy);x++;y++;}}
}
大題:請用整數化的中點畫線算法計算直線(0,0)(5,3)的掃描轉換結果,并給出計算流程表。
答:
根據整數化的中點畫線算法,我們首先計算初始值:
- d x = 5 ? 0 = 5 dx = 5 - 0 = 5 dx=5?0=5
- d y = 3 ? 0 = 3 dy = 3 - 0 = 3 dy=3?0=3
- d = d x ? 2 d y = 5 ? 2 ? 3 = ? 1 d = dx - 2 dy = 5 - 2*3 = -1 d=dx?2dy=5?2?3=?1
然后,我們根據算法步驟逐步更新 x x x, y y y,和 d d d 的值:
| x | y | d | d是否大于0? | 更新操作 |
|---|---|---|---|---|
| 0 | 0 | -1 | 否 | d = d + 2 d x ? 2 d y = ? 1 + 10 ? 6 = 3 d = d + 2dx - 2dy = -1 + 10 - 6 = 3 d=d+2dx?2dy=?1+10?6=3 |
| 1 | 1 | 3 | 是 | d = d ? 2 d y = 3 ? 6 = ? 3 d = d - 2dy = 3 - 6 = -3 d=d?2dy=3?6=?3 |
| 2 | 1 | -3 | 否 | d = d + 2 d x ? 2 d y = ? 3 + 10 ? 6 = 1 d = d + 2dx - 2dy = -3 + 10 - 6 = 1 d=d+2dx?2dy=?3+10?6=1 |
| 3 | 2 | 1 | 是 | d = d ? 2 d y = 1 ? 6 = ? 5 d = d - 2dy = 1 - 6 = -5 d=d?2dy=1?6=?5 |
| 4 | 2 | -5 | 否 | d = d + 2 d x ? 2 d y = ? 5 + 10 ? 6 = ? 1 d = d + 2dx - 2dy = -5 + 10 - 6 = -1 d=d+2dx?2dy=?5+10?6=?1 |
| 5 | 3 | - | - | - |
注意:在每一步中, x x x 都會增加 1 1 1,但 y y y 是否增加取決于 d d d 的值。
圓的掃描轉換
考慮以坐標系原點為圓心,半徑為 r r r 的圓。則圓周上各點滿足 x 2 + y 2 = r 2 x^2+y^2=r^2 x2+y2=r2,也就是說:
F ( x , y ) = x 2 + y 2 ? r 2 = 0 F(x, y) = x^2+y^2 - r^2 = 0 F(x,y)=x2+y2?r2=0
這也稱為圓的隱方程。
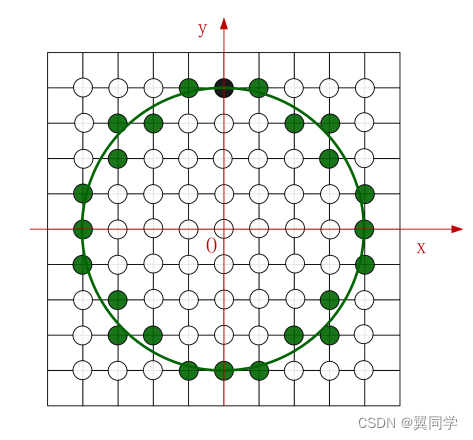
圓分平面成三個區域:
- 對于圓上的點, F ( x , y ) = 0 F(x,y)=0 F(x,y)=0;
- 對于圓外的點, F ( x , y ) > 0 F(x,y)>0 F(x,y)>0;
- 對于圓內的點, F ( x , y ) < 0 F(x,y)<0 F(x,y)<0。
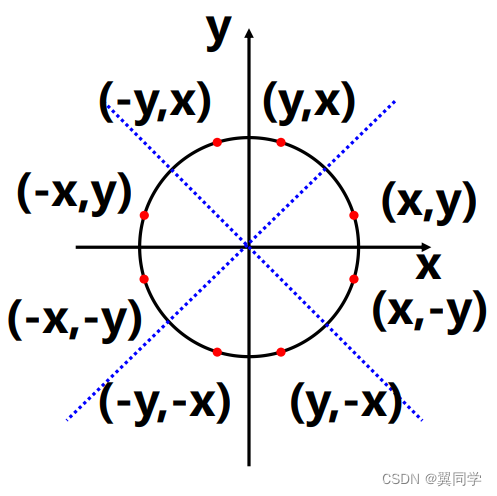
圓的八對稱性:只要掃描轉換八分之一圓弧,
就可以求出整個圓弧的像素集。
因為圓關于坐標軸和對角線對稱。
中點畫圓算法
中點畫圓算法流程如下::
int x = 0;
int y = r;
double d = 1.25 - r;while (x < y) { // 當 x = y 時結束plotCirclePoints(x, y);if (d >= 0) {d += 2 * (x - y) + 5;y--;} else {d += 2 * x + 3;}x++;
}
填空題:根據圓的八對稱性,我們在掃描轉換半徑為R的圓形的時候,選擇掃描轉換圓心在【】,以(【】,【】)為起點,以【】為結束條件的圓弧,并且在掃描轉換過程中,每一步畫點的時候,一次畫出【】個點。
答:
- 【原點】
- 【0】
- 【R】
- 【x=y】
- 【8】
大題:使用中點畫圓的掃描轉換算法,掃描轉換圓心在(0,0),半徑為6的圓,按照算法流程給出每一步計算的誤差D和Y坐標。
答:
根據中點畫圓算法的描述,我們可以逐步計算每一步的 x x x, y y y 坐標和誤差 d d d 的值。

圓的半徑 r = 6 r = 6 r=6,所以初始值為:
- x = 0 x = 0 x=0
- y = r = 6 y = r = 6 y=r=6
- d = 1.25 ? r = 1.25 ? 6 = ? 4.75 d = 1.25 - r = 1.25 - 6 = -4.75 d=1.25?r=1.25?6=?4.75
接下來,我們將按照算法步驟進行迭代。每次 d d d 的更新依賴于它是正還是負:
- 如果 d ≥ 0 d \ge 0 d≥0,則 d = d + 2 ( x ? y ) + 5 d = d + 2 (x - y) + 5 d=d+2(x?y)+5,此時 y y y 減 1 1 1
- 如果 d < 0 d < 0 d<0,則 d = d + 2 x + 3 d = d + 2 x + 3 d=d+2x+3,此時 y y y 不變
因此:
| x x x | y y y | d d d | d d d 是否 ≥ 0 \ge 0 ≥0? | 更新操作 |
|---|---|---|---|---|
| 0 0 0 | 6 6 6 | ? 4.75 -4.75 ?4.75 | 否 | d = d + 2 x + 3 = ? 4.75 + 3 = ? 1.75 d = d + 2x + 3 = -4.75+ 3 = -1.75 d=d+2x+3=?4.75+3=?1.75 |
| 1 1 1 | 6 6 6 | ? 1.75 -1.75 ?1.75 | 否 | d = d + 2 x + 3 = ? 1.75 + 2 × 1 + 3 = 3.25 d = d + 2x + 3 = -1.75 + 2×1 + 3 = 3.25 d=d+2x+3=?1.75+2×1+3=3.25 |
| 2 2 2 | 6 6 6 | 3.25 3.25 3.25 | 是 | d = d + 2 ( x ? y ) + 5 = 3.25 + 2 ( 2 ? 6 ) + 5 = 0.25 d = d + 2(x - y) + 5 = 3.25 + 2(2-6) + 5 = 0.25 d=d+2(x?y)+5=3.25+2(2?6)+5=0.25,同時 y = y ? 1 y = y - 1 y=y?1 |
| 3 3 3 | 5 5 5 | 0.25 0.25 0.25 | 是 | d = d + 2 ( x ? y ) + 5 = 0.25 + 2 ( 3 ? 5 ) + 5 = 1.25 d = d + 2(x - y) + 5 = 0.25 + 2(3 - 5) + 5 = 1.25 d=d+2(x?y)+5=0.25+2(3?5)+5=1.25,同時 y = y ? 1 y = y - 1 y=y?1 |
| 4 4 4 | 4 4 4 |
當 x = y x = y x=y 時,算法結束。
單選題:Bresenham圓掃描轉換法中,初始誤差 d 為?(B)
A.2-r
B. 3-2*r
C. 1-r
D. r
單選題:Bresenham圓的掃描轉換算法的算法結束條件是( A)。
A.x==y
B. x=1
C. y=1
D. x!=y
反走樣
- 【走樣】:在連續空間中的物體映射到圖像空間帶來的各種各樣的失真。
- 【反走樣】:用于減少和消除各種走樣的方法。
反走樣的技術:
硬件:提高顯示器的分辨率
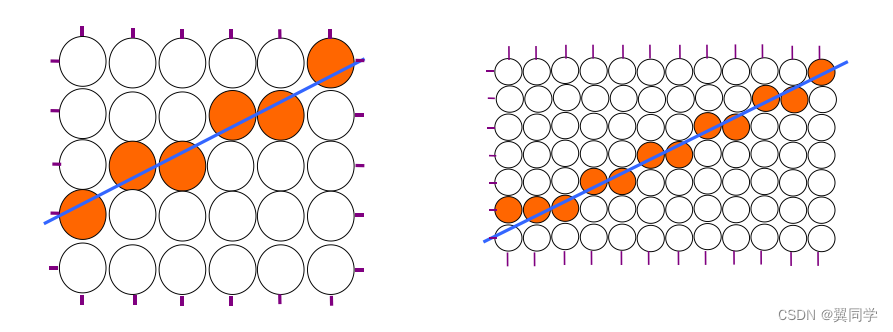
軟件:改進軟件算法。比如下面這個【加權區域采樣】:
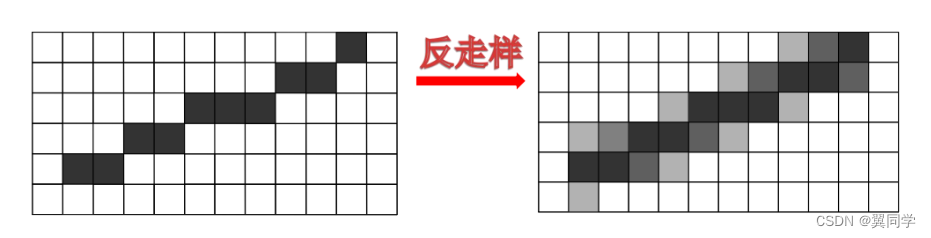
加權區域采樣(距離,面積,體積),原理是利用人眼視覺特性,即人眼對某一區域顏色的識別是這個區域顏色的平均值。
通過加權平均的方法,調節像素的亮度和灰度,以產生模糊的邊界,從而達到較好的視覺效果以消除“鋸齒”。
另外還有【Wu反走樣】:
武筱林于1991年在computer Graphics上提出 “Efficient Antialiasing Technique”。
Wu反走樣算法原理是對于理想直線上的任一點,同時以兩個不同亮度級別的相鄰像素來表示。
單選題:下列不屬于走樣現象的有?(D)
A.階梯現象
B.動畫閃爍
C.亮度不均
D.深度丟失
單選題:下面關于反走樣的方法中論述錯誤的是( D )
A.提高分辨率
B.把像素當作平面區域進行采樣
C.采用特定形狀的濾波器進行加權區域采樣
D. 增強圖像的顯示亮度
單選題:如果背景顏色為(100,0,100),直線顏色為(200,200,100),反走樣算法計算的前景色比率為0.2,則像素點的顏色?(C)
A.(180,160,100)
B.(150,100,100)
C.(120,40,100)
D.以上都不對
解析:
- 定義背景顏色 C b g = ( R b g , G b g , B b g ) C_{bg} = (R_{bg}, G_{bg}, B_{bg}) Cbg?=(Rbg?,Gbg?,Bbg?)
- 定義前景顏色 C f g = ( R f g , G f g , B f g ) C_{fg} = (R_{fg}, G_{fg}, B_{fg}) Cfg?=(Rfg?,Gfg?,Bfg?)
- 定義前景色比率為 α \alpha α,則背景色比率為 1 ? α 1 - \alpha 1?α
- 最終顏色 C = ( R , G , B ) C = (R, G, B) C=(R,G,B)
則:
C = C b g ? ( 1 ? α ) + C f g ? α C = C_{bg} \cdot (1 - \alpha) + C_{fg} \cdot \alpha C=Cbg??(1?α)+Cfg??α
也就是說:
- R = R b g ? ( 1 ? α ) + R f g ? α R = R_{bg} \cdot (1 - \alpha) + R_{fg} \cdot \alpha R=Rbg??(1?α)+Rfg??α
- G = G b g ? ( 1 ? α ) + G f g ? α G = G_{bg} \cdot (1 - \alpha) + G_{fg} \cdot \alpha G=Gbg??(1?α)+Gfg??α
- B = B b g ? ( 1 ? α ) + B f g ? α B = B_{bg} \cdot (1 - \alpha) + B_{fg} \cdot \alpha B=Bbg??(1?α)+Bfg??α
對于給定的問題,將數值代入:
- R = 100 ? ( 1 ? 0.2 ) + 200 ? 0.2 = 120 R = 100 \cdot (1 - 0.2) + 200 \cdot 0.2 = 120 R=100?(1?0.2)+200?0.2=120
- G = 0 ? ( 1 ? 0.2 ) + 200 ? 0.2 = 40 G = 0 \cdot (1 - 0.2) + 200 \cdot 0.2 = 40 G=0?(1?0.2)+200?0.2=40
- B = 100 ? ( 1 ? 0.2 ) + 100 ? 0.2 = 100 B = 100 \cdot (1 - 0.2) + 100 \cdot 0.2 = 100 B=100?(1?0.2)+100?0.2=100
因此,最終顏色 C = ( 120 , 40 , 100 ) C = (120, 40, 100) C=(120,40,100)。
單選題:產生走樣的根本原因是( D )。
A.顯示分辨率太低
B. 圖像數據量太大
C. 顯存太小
D .像素是有大小的,離散的,不是理想的數學上的點
判斷題:確定最佳逼近圖形的像素集合,并用指定屬性寫像素的過程稱為圖形的掃描轉換或光柵化。(正確)
判斷題:圖形學中的直線是沒有寬度和端點的。(正確)
簡答題:走樣的現象能不能完全消除?反走樣的概念是什么?
答:
不能完全消除。
將定義在連續空間中的物體映射到圖像空間帶來的各種各樣的失真稱為走樣,用于減少和消除各種走樣的方法叫做反走樣。
第三章 多邊形填充
概念
多邊形填充的定義:將一個多邊形區域內每個像素點繪制上某種顏色的過程。
多邊形的表示方法:
- 頂點表示:用多邊形的頂點序列來表示多邊形
- 點陣表示:用位于多邊形內的像素點的集合來刻畫多邊形
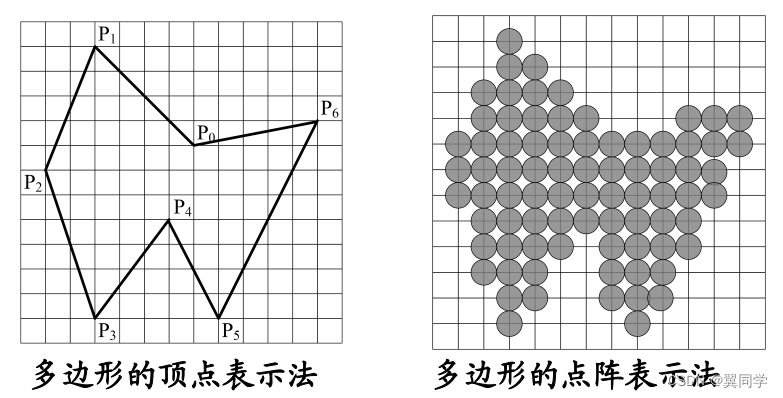
多邊形掃描轉換的基本思想:
- 對于一個多邊形,用一組水平或垂直的掃描線進行掃描,求出每條掃描線與多邊形的交點.
- 這些交點將掃描線分割線段
- 將落在多邊形內的所有線段上的每個像素點賦以給定的多邊形填充色。
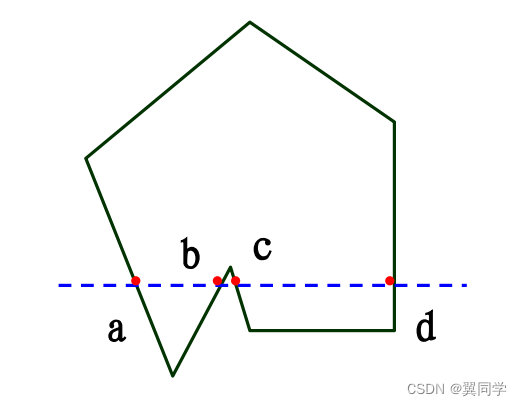
區域是指相互連通的一組像素的集合,一般由封閉的區域邊界定義。
區域填充一般采用種子填充算法,從區域內給定的種子像素出發,按填充顏色填充種子的相鄰像素,直到邊界為止。
單選題:多邊形掃描轉換可以將(A )。
A. 多邊形由頂點表示轉換成點陣表示
B.多邊形由區域表示轉換成邊界表示
C.多邊形轉換為顯示器的掃描線
D.多邊形的填充屬性改變
有效邊表的填充思路
算法思路:
- 確定多邊形所占有的最大掃描線數,得到多邊形頂點的最小和最大y值( y m i n y_{min} ymin? 和 y m a x y_{max} ymax? )
- 從 y = y m i n y = y_{min} y=ymin? 到 y = y m a x y = y_{max} y=ymax? 進行掃描,每一次用一條掃描線進行填充
- 對一條掃描線填充的過程可分為四個步驟:
- 求交:掃描線與多邊形各邊的交點
- 排序:把掃描線上所有交點按x遞增順序進行排序
- 交點配對:將排序后的交點進行兩兩配對,每對交點代表掃描線與多邊形的一個相交區間
- 區間填色:把區間內的像素置為填充色
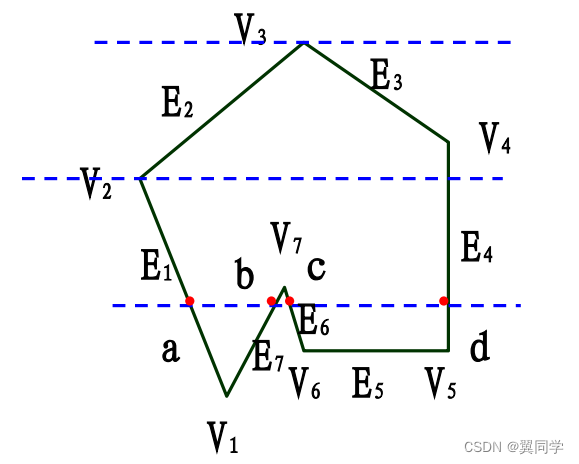
單選題:在X-掃描線算法中,每次用一條掃描線進行填充,對一條掃描線填充的過程可以分為哪四個步驟?(A)
A.求交,排序,配對,填色
B.排序,求交,配對,填色
C.求交,配對,排序,填色
D.排序,填色,求交,配對
有效邊表的算法實現
有效邊表填充算法用 ET 邊表和 AET 活動邊表來實現。
邊表(ET)是用來對除水平邊外的所有邊進行登記,來建立邊的記錄,內容如下:
| x / y m i n x/y_{min} x/ymin? | y m a x y_{max} ymax? | 1 / k 1/k 1/k | next |
|---|
其中:
- x / y m i n x/y_{min} x/ymin?:邊的最小的 y y y對應的 x x x值
- y m a x y_{max} ymax?:邊的最大 y y y值
- 1 / k 1/k 1/k:邊斜率的倒數
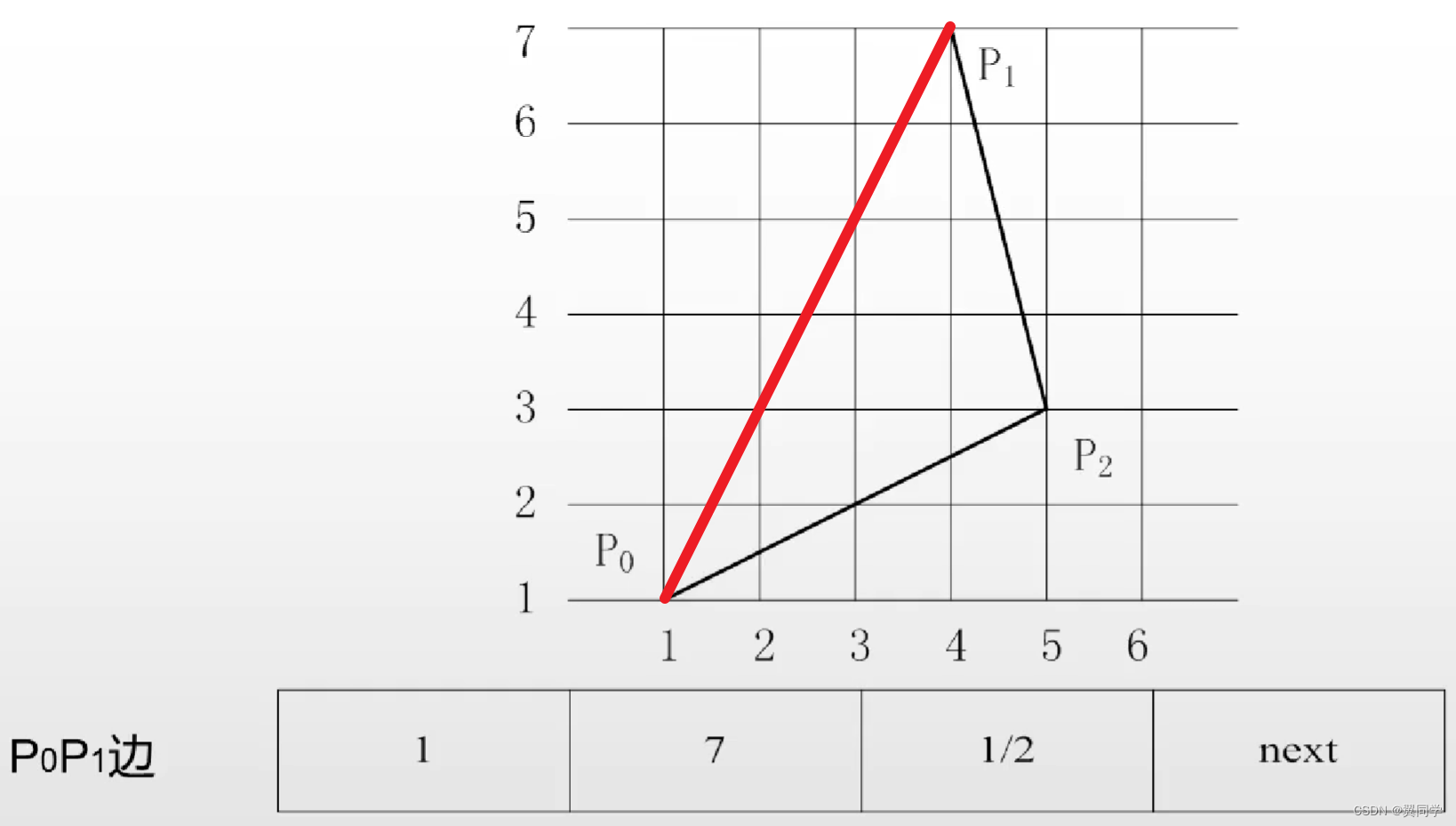
比如在上述圖形中,對于 P 0 P 1 P_0P_1 P0?P1? 邊的ET表來說,邊的最小的 y y y對應的 x x x值為 1 1 1,邊的最大 y y y值為 7 7 7,邊斜率的倒數就是 1 / 2 1/2 1/2。
那么,當知道怎么求ET 表建立以后,就可以開始掃描轉換了。
從 y = y m i n y = y_{min} y=ymin? 到 y = y m a x y = y_{max} y=ymax? 進行掃描,每一次用一條掃描線進行填充。
對不同的掃描線,與之相交的邊線也是不同的。
當對某一條掃描線進行掃描轉換時,我們只需要考慮與它相交的那些邊線,為此需要建立一個只與當前掃描線相交的邊記錄鏈表,稱之為活動邊表(AET表)。
AET 表的建立過程就是有效地進行填充的操作。
舉個例子吧:
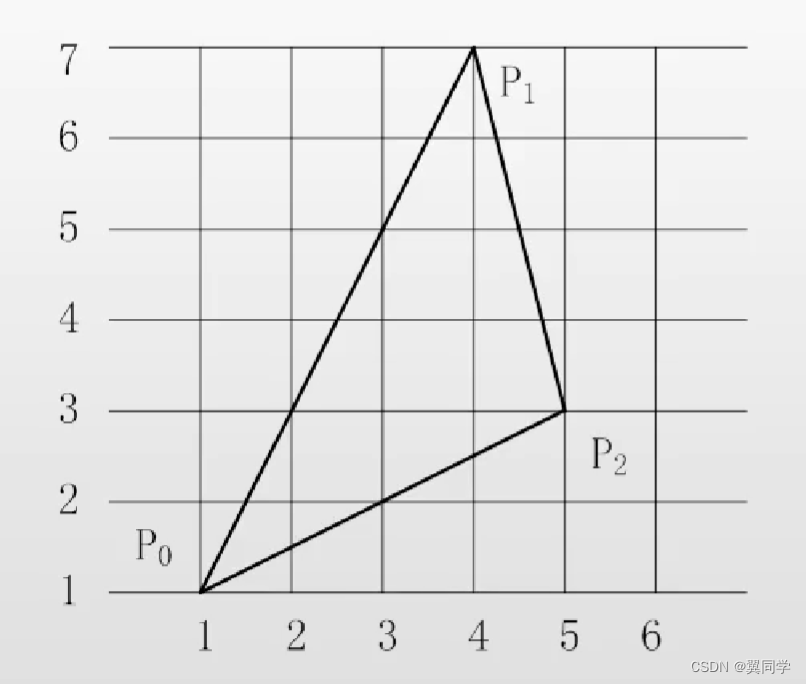
從 y = y m i n = 1 y = y_{min} = 1 y=ymin?=1 開始,掃描到 y = y m a x = 7 y = y_{max} = 7 y=ymax?=7,如果一條邊的最低點第一次落到掃描邊上,那么,就把該邊添加到 AET 活動邊表中。
因此上圖生成的 AET 表如下:

注意:當掃描線與多邊形相交,同時交點又是頂點時:
- 普通連接點的頂點個數計數為1
- 局部最低點的頂點個數計為2
- 局部最高點的頂點個數計為0
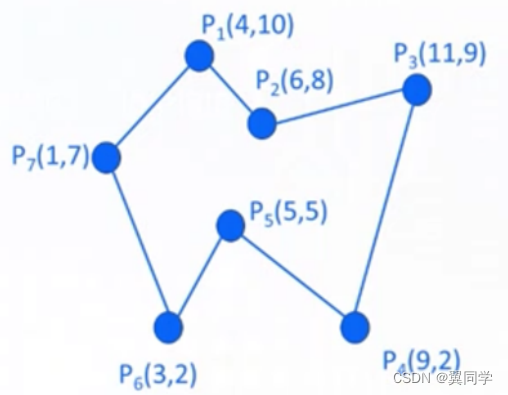
大題:使用有效邊表的填充算法填充下面的多邊形。
- 問題1:請問,各頂點處會與水平掃描線產生幾個交點?
- 問題2:給出多邊形的邊 P 6 P 7 P_6P_7 P6?P7? 的邊表信息。
答:
問題1:
| P 1 P_1 P1? | P 2 P_2 P2? | P 3 P_3 P3? | P 4 P_4 P4? | P 5 P_5 P5? | P 6 P_6 P6? | P 7 P_7 P7? |
|---|---|---|---|---|---|---|
| 0 | 2 | 0 | 2 | 0 | 2 | 1 |
問題2:
| 3 3 3 | 7 7 7 | ? 2 5 - \frac{2}{5} ?52? | next |
|---|
大題:使用有效邊表填充算法對下面的多邊形進行填充,填寫空(1)~ 空(15):
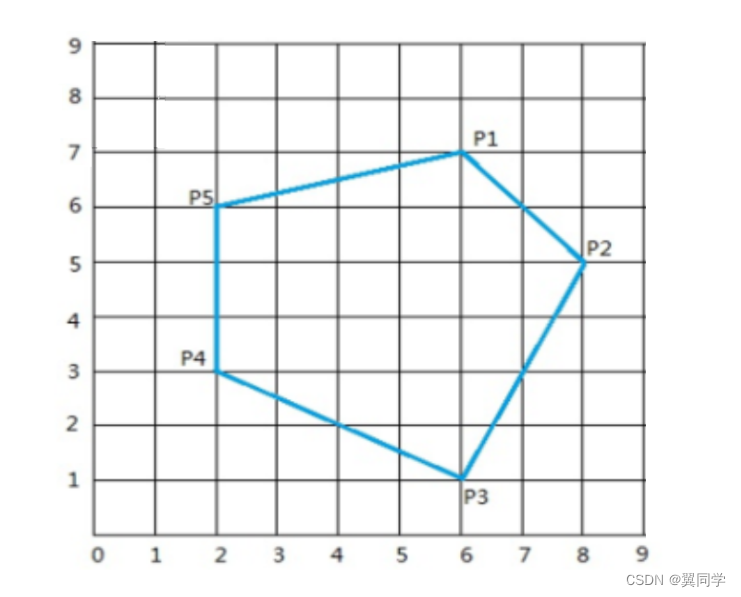
ET表:
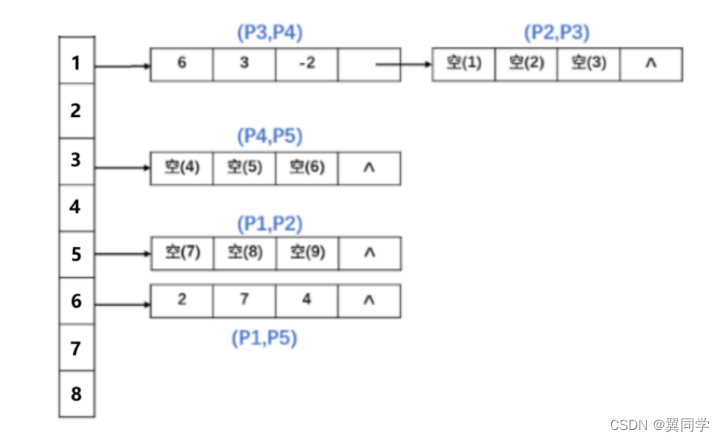
問題1:請問 y = 2 y = 2 y=2 掃描線上的填充區間是(空(10),2) ~ (空(11), 2)
問題2:下圖是 y = 3 y = 3 y=3 時的 AET 表,請填充其中缺少的空:

問題3:算法在 P 1 P_1 P1? 點處計算 空(15) 個交點。
答:
- 空1:【6】
- 空2:【5】
- 空3:【1/2】
- 空4:【2】
- 空5:【6】
- 空6:【0】
- 空7:【8】
- 空8:【7】
- 空9:【-1】
- 空10:【4】
- 空11:【7】
- 空12:【7】
- 空13:【5】
- 空14:【1/2】
- 空15:【0】
單選題:邊表應記錄的內容不包括下面哪一項?( C )
A.最小的y對應的x值
B. 最大的y
C. 最小的y
D. 斜率的倒數
單選題:對下圖進行基于掃描線的區域填充,在掃描線5上要填充的區間為?(B)
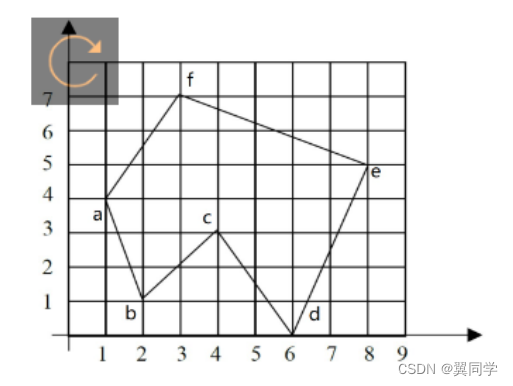
A.(1,5)到(8,5)
B. (2,5)到(8,5)
C(1.7,5)到(8,5)
D.以上都不對
單選題:對下圖進行基于掃描線的區域填充,在掃描線6上要填充的區間為?(A)

A.(2,6)到(6,6)
B(1,6)到(6,6)
C(2,6)到(5,6)
D.以上都不對
單選題:如下圖所示,對 cd 邊建立邊表對應的三項內容應該是?(A)

A. 6,3,-2/3
B. 6,2,-2/3
C. 6,3,-3/2
D. 6,2,-3/2
判斷題:有效邊表填充算法中邊表(ET)里的 x / y m i n x/y_{min} x/ymin? 表示x的最小值。(錯誤)
邊緣填充
- 算法思路:利用取補運算代替交點排序、配對、構造填充區間。
- 算法原理:
- 像素點顏色值經過偶數次取補運算后保持不變
- 像素點顏色值經過奇數次取補運算后變為其補數
- 算法分類:
- 以掃描線為中心的邊填充算法:對于每一條掃描線和每條多邊形邊的交點 ( x 1 , y 1 ) (x1,y1) (x1,y1) ,將該掃描線上交點右方的所有像素取補,對每條掃描線做此處理,交點處理的順序隨意。
- 以邊為中心的邊填充算法:將每條非水平邊右側的像素取補,邊的處理順序隨意。
單選題:關于邊緣填充算法,描述正確的是:(B)
A.一個像素經過偶數次的取補會變成它的補色
B.一個像素經過奇數次的取補會變成它的補色
C.一個像素是前景色經過取補運算保持不變
D.取補運算是對像素的坐標進行變換
判斷題:關于邊緣填充算法里的取補運算,一個像素經過偶數次的取補會變成它的補色。(錯誤)
種子填充算法
- 連通區域:
- 4連通區域是指從區域內一點出發,通過上、下、左、右四種運動可到達區域內的任一像素點。
- 8連通區域是指從區域內一點出發,通過上、下、左、右以及對角線方向的八種運動可到達區域內的每一像素點。
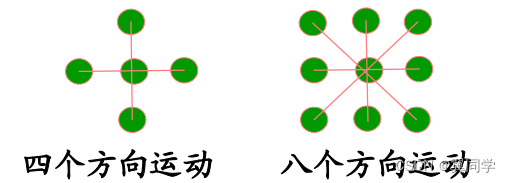
以四連通區域的填充為例,種子填充算法的思路是:
- 初始化:將種子像素壓入棧中。
- 循環檢查:
- 如果棧為空,則算法結束。
- 如果棧不為空,執行以下步驟:
a. 從棧中彈出一個像素。
b. 將該像素置為填充色。
c. 檢查該像素相鄰的四連通像素是否為邊界色或已經置為填充色。如果不是,將這些像素壓入棧中。
- 重復步驟2,直到棧為空。
- 結束:所有可達的非邊界且未填充的像素都已被填充。
public void floodFill(int[][] image, Point seed, int fillColor, int boundaryColor) {Stack<Point> stack = new Stack<>();stack.push(seed); // 初始化:將種子像素壓入棧中while (!stack.isEmpty()) { // 循環檢查Point current = stack.pop(); // 從棧中彈出一個像素int x = current.x;int y = current.y;// 檢查當前像素是否越界或已經是填充色或邊界色if (x < 0 || x >= image[0].length || y < 0 || y >= image.length || image[y][x] == fillColor || image[y][x] == boundaryColor) {continue;}image[y][x] = fillColor; // 將該像素置為填充色// 檢查相鄰的四連通像素并壓入棧中stack.push(new Point(x + 1, y));stack.push(new Point(x - 1, y));stack.push(new Point(x, y + 1));stack.push(new Point(x, y - 1));}// 結束:所有可達的非邊界且未填充的像素都已被填充
}
單選題:種子填充算法中,正確的敘述是?(C)
A.它是按掃描線的順序進行像素點的填充
B. 四連接算法可以填充八連接區域
C.四連接區域內的每一像素可以通過上下左右四個方向組合到達
D.八連接算法不能填充四連通區域。
對下圖實施四連通種子填充,其中 S 點為種子。將種子出棧后接下來需要將以下哪些元素入棧?(C)
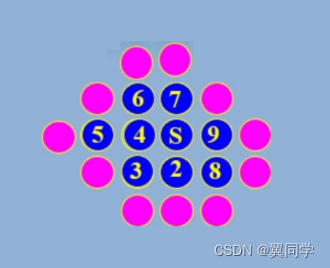
A.2,4
B.7,9
C. 2,4,7,9
D.以上都不對
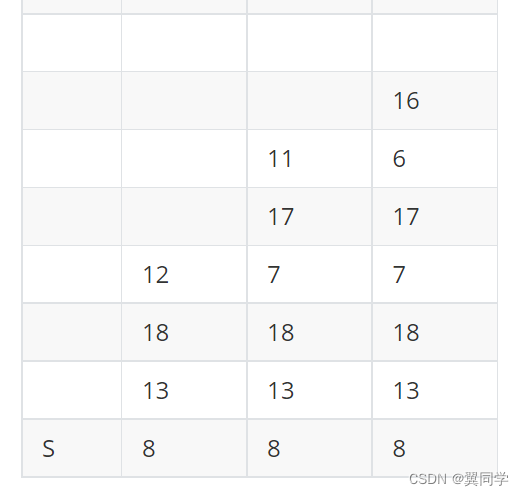
大題:如下圖所示的多邊形區域,使用四連通種子填充算法進行填充,按照上右下左的順序遍歷鄰接像素點:
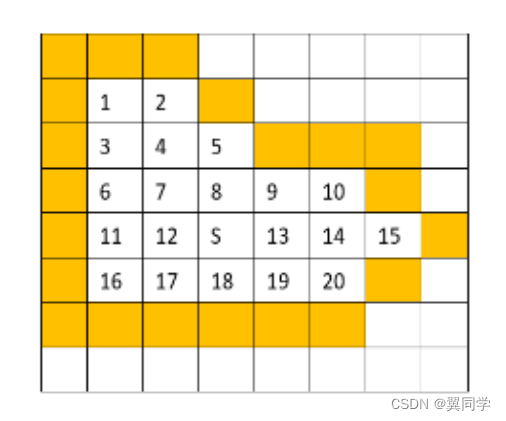
下面是該算法在運行過程中的堆棧信息:
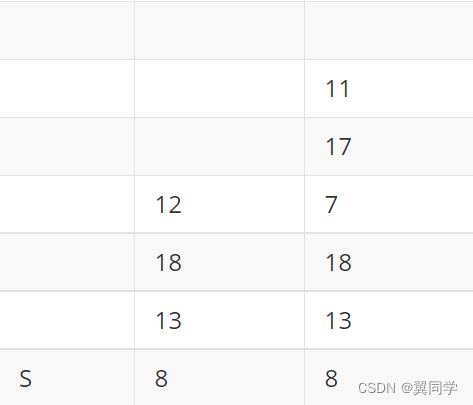
請給出算法下一步執行過程堆棧的內容(按順序從棧頂元素開始回答)。
其中, S S S 像素點是選取的種子點,用像素的編號代表像素。
答:
題目說了,按照上右下左的順序遍歷鄰接像素點。由于此時棧頂元素為 11 11 11,把 11 11 11 彈出來之后,標記為已經訪問,然后按照上右下左的順序,看看有沒有哪個像素點還沒有訪問過:
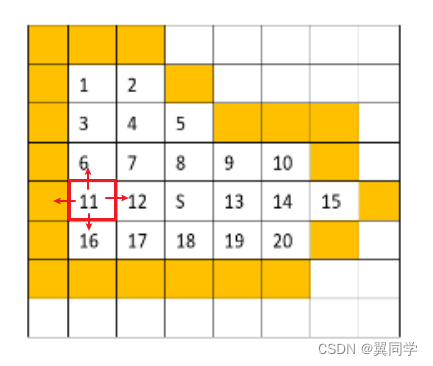
此時發現, 6 6 6和 16 16 16都沒有訪問過,所以 6 6 6先壓入棧、然后再壓入 16 16 16。答案為:





)













