概述
通過指定平面上的多個點,然后順次連接,我們可以得到折線段,如果閉合圖形,就可以獲得多邊形。通過向量旋轉我們可以獲得圓等特殊圖形。
但是對于任意曲線,我們無法使用簡單的方式來獲取其頂點,好在計算機大神們已經發明了貝塞爾曲線這樣的算法。
本篇就介紹如何在Godot中繪制貝塞爾曲線,并通過設定控制點來精確控制曲線的走向。
(原文寫于2024年4月,內容持續改進和擴充中)
基礎原理
在實際上手繪制之前,讓我們先來理解一下貝塞爾曲線的求點原理與本質——向量插值。
二次貝塞爾曲線
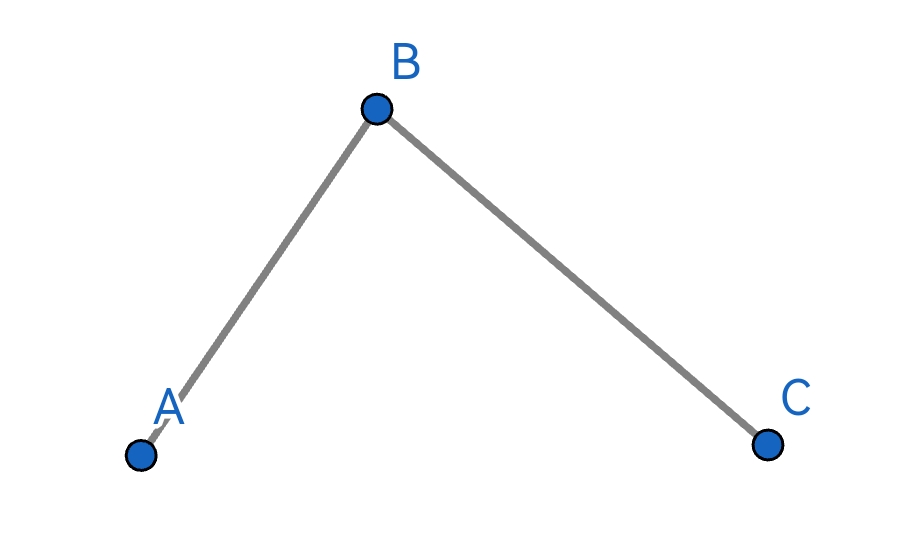
在平面上有三個點A、B、C:
- AB相連,形成一個向量 A B ? \vec{AB} AB,BC相連,形成另一個向量 B C ? \vec{BC} BC;
- 對 A B ? \vec{AB} AB和 B C ? \vec{BC} BC同步進行
0.0到1.0插值,設插值變量為t。 - 在插值的每一時刻,會從 A B ? \vec{AB} AB和 B C ? \vec{BC} BC上各獲得一個點
D和E。
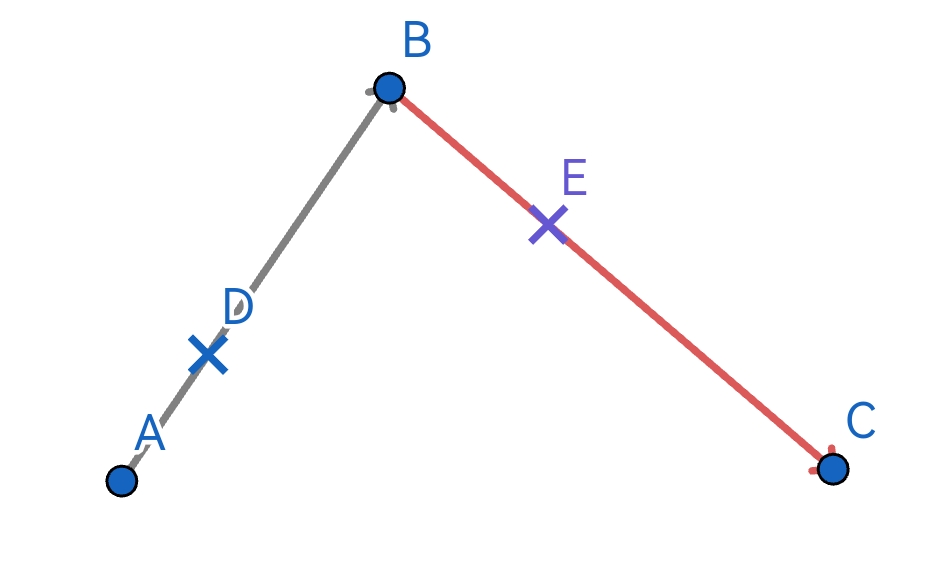
- 連接DE,對 D E ? \vec{DE} DE進行
0.0到1.0插值,而且插值與此時的t一致。則獲得一個點F。 - 也就是說,同步對 A B ? \vec{AB} AB和 B C ? \vec{BC} BC、 D E ? \vec{DE} DE進行
0.0到1.0插值。
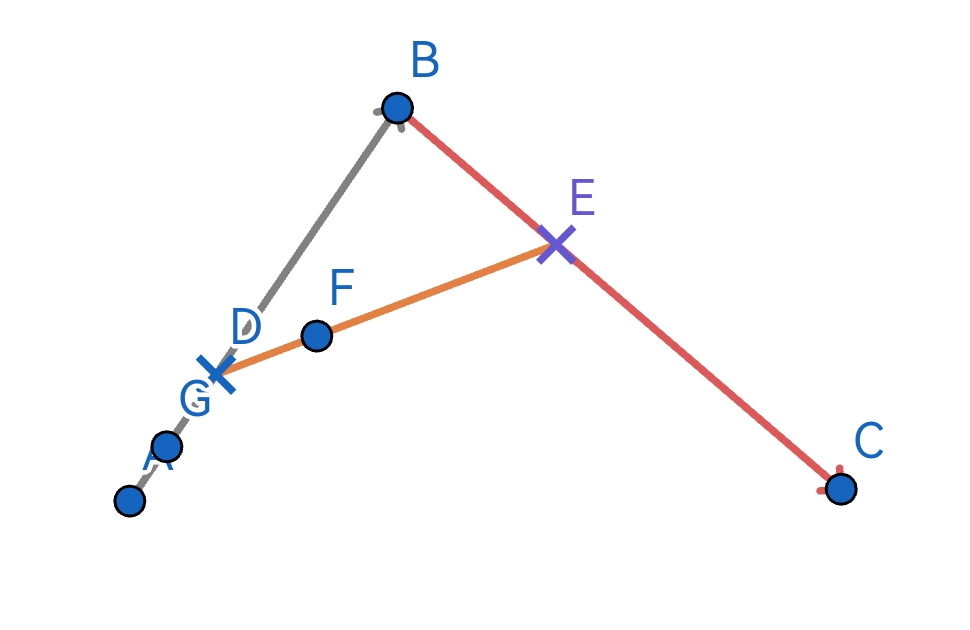
從 D E ? \vec{DE} DE插值獲取的所有點F連起來就是一條由A到B的貝塞爾曲線。整個插值過程也就是官方文檔中的這張動圖:
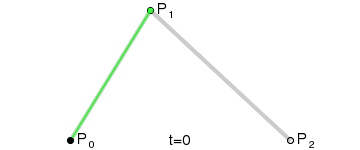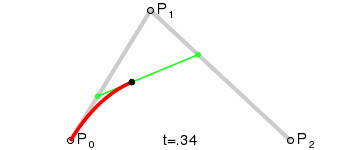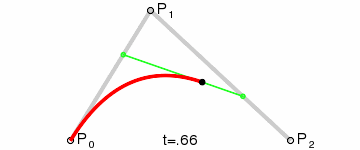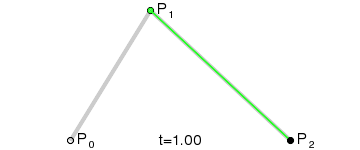
所以二次貝塞爾曲線是同時進行三個向量插值獲得的點的集合。
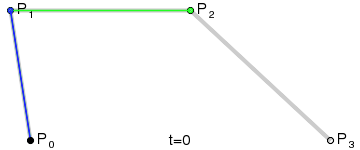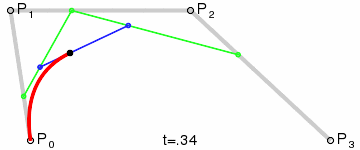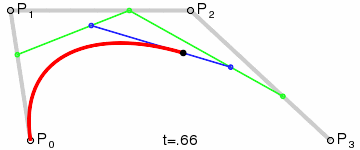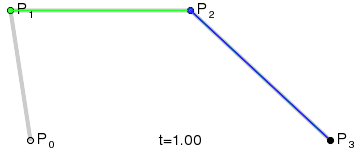
三次貝塞爾曲線
平面上四個點A、B、C、D:
- 分別組成三個向量 A B ? \vec{AB} AB、 B C ? \vec{BC} BC和 C D ? \vec{CD} CD
- 在三個向量上同步插值獲得三個點E、F、G
- EF和FG相連,組成向量 E F ? \vec{EF} EF、 F G ? \vec{FG} FG
- 在 E F ? \vec{EF} EF、 F G ? \vec{FG} FG上同步插值獲得點H和I
- E F ? \vec{EF} EF上同步插值獲得點J
- 整個同步插值過程獲得的點J的集合,順序相連,繪制處的就是三次貝塞爾曲線。
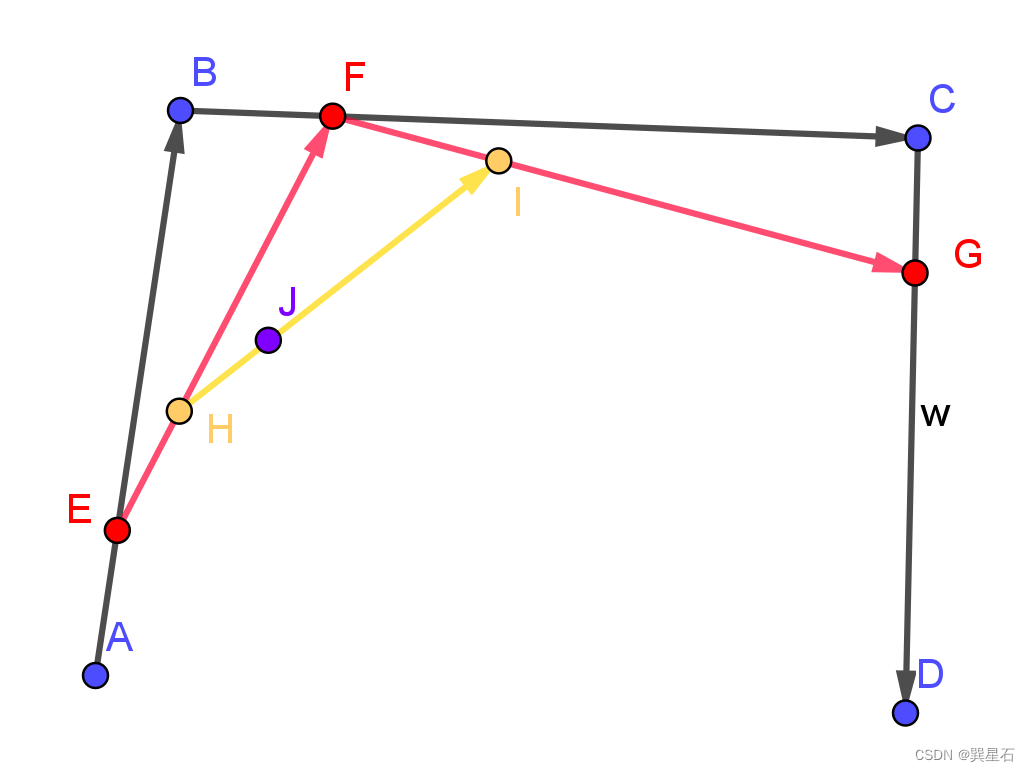
動態過程如下(也就是官方文檔的動圖):
在Godot中實際繪制貝塞爾曲線
在Godot中實際上并不需要我們編寫自己的貝塞爾曲線插值求點函數,Vector2類型的bezier_interpolate()方法可以讓我們輕松的獲取相應頂點和控制點設置下的貝塞爾曲線點。它的定義如下:
bezier_interpolate(control_1: Vector2, control_2: Vector2, end: Vector2, t: float) -> Vector2
control_1和control_2分別為控制點1和控制點2end可以理解為第二個點t是0.0到1.0的插值,也可以理解為一個百分比或偏移量
bezier_interpolate()的用法就是:
p1.bezier_interpolate(c1,c2,p2,t)
其中:
p1是貝塞爾曲線起點,p2是貝塞爾曲線終點c1,c2分別為控制點1和控制點2t是百分比
所以我們想要求一段貝塞爾曲線,就需要指定4個點,其中2個是起止點,另外2個是控制點。并使用一個for循環來進行插值,求取整個過程中的點。
最后再使用Godot內置的繪圖函數draw_polyline()來繪制。
我們看一個實例:
extends Node2Dvar p1 = Vector2(100,100) # 起點
var p2 = Vector2(200,200) # 終點
var ctl_1 = Vector2(100,0) # 控制點1
var ctl_2 = Vector2(100,0) # 控制點2var points:PackedVector2Array = [] # 曲線點集合
var steps = 100; # 點的數目,越多曲線越平滑var curve_color:= Color.WHITE # 曲線繪制顏色
var ctl_color:= Color.AQUAMARINE # 控制點和連線繪制顏色func _ready() -> void:# 求曲線點集for i in range(steps+1):var p = p1.bezier_interpolate(p1+ctl_1,p2-ctl_2,p2,i/float(steps))points.append(p)func _draw() -> void:# 繪制控制點draw_arc(p1+ctl_1,2,0,TAU,10,ctl_color,1)draw_arc(p2-ctl_2,2,0,TAU,10,ctl_color,1)# 繪制曲線端點與控制點的連線draw_line(p1,p1+ctl_1-Vector2(1,0),ctl_color,1)draw_line(p2,p2-ctl_1+Vector2(1,0),ctl_color,1)# 繪制貝塞爾曲線draw_polyline(points,curve_color,1)
上面的代碼中:
- 我們首先聲明變量保存起點、終點和兩個控制點的坐標
- 然后申明變量
points用于存儲插值獲取的貝塞爾曲線上的點 steps變量用于存儲總共插值的步數,也就是獲得的曲線上點的個數,步數越多,求得的點越多,最終繪制的曲線越平滑- 申明兩個變量來分別存儲曲線和控制點的顏色。
- 在
_ready()中我們執行一個for循環來插值steps次,來獲取指定的起點、終點、控制點下的貝塞爾曲線上的點,并存儲到變量points中 - _draw()在場景運行時會被自動調用,用來實際的繪制出曲線和控制點
最終繪制結果如下:
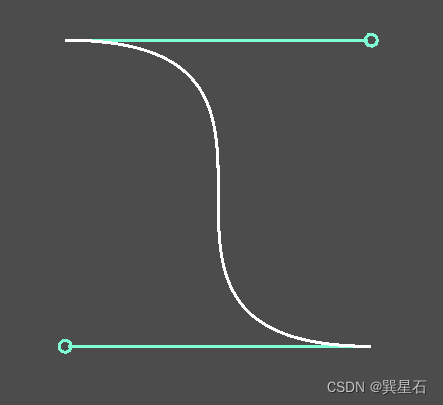
導數
Vector2類型提供了一個名叫bezier_derivative()的方法,用來求貝塞爾曲線上t處的“導數”。
經過實際測試,這個所謂的“導數”是一個點,連接貝塞爾曲線上t處的點與該點,剛好是一個切線段。
我們以下面的代碼進行測試:
extends Node2Dvar p1 = Vector2(100,100) # 起點
var p2 = Vector2(200,200) # 終點
var ctl_1 = Vector2(50,0) # 控制點1
var ctl_2 = Vector2(50,0) # 控制點2var points:PackedVector2Array = [] # 曲線點集合
var ds:PackedVector2Array = [] # 曲線點導數集合
var steps = 100; # 點的數目,越多曲線越平滑var curve_color:= Color.WHITE # 曲線繪制顏色
var ctl_color:= Color.AQUAMARINE # 控制點和連線繪制顏色func _ready() -> void:# 求曲線點集for i in range(steps+1):var p = p1.bezier_interpolate(p1+ctl_1,p2-ctl_2,p2,i/float(steps))points.append(p)var d = p1.bezier_derivative(p1+ctl_1,p2-ctl_2,p2,i/float(steps))ds.append(d)func _draw() -> void:draw_polyline(points,curve_color,1)var i = 0draw_line(points[i],points[i]+ds[i],ctl_color,1)print(points[i]," ",points[i]+ds[i])
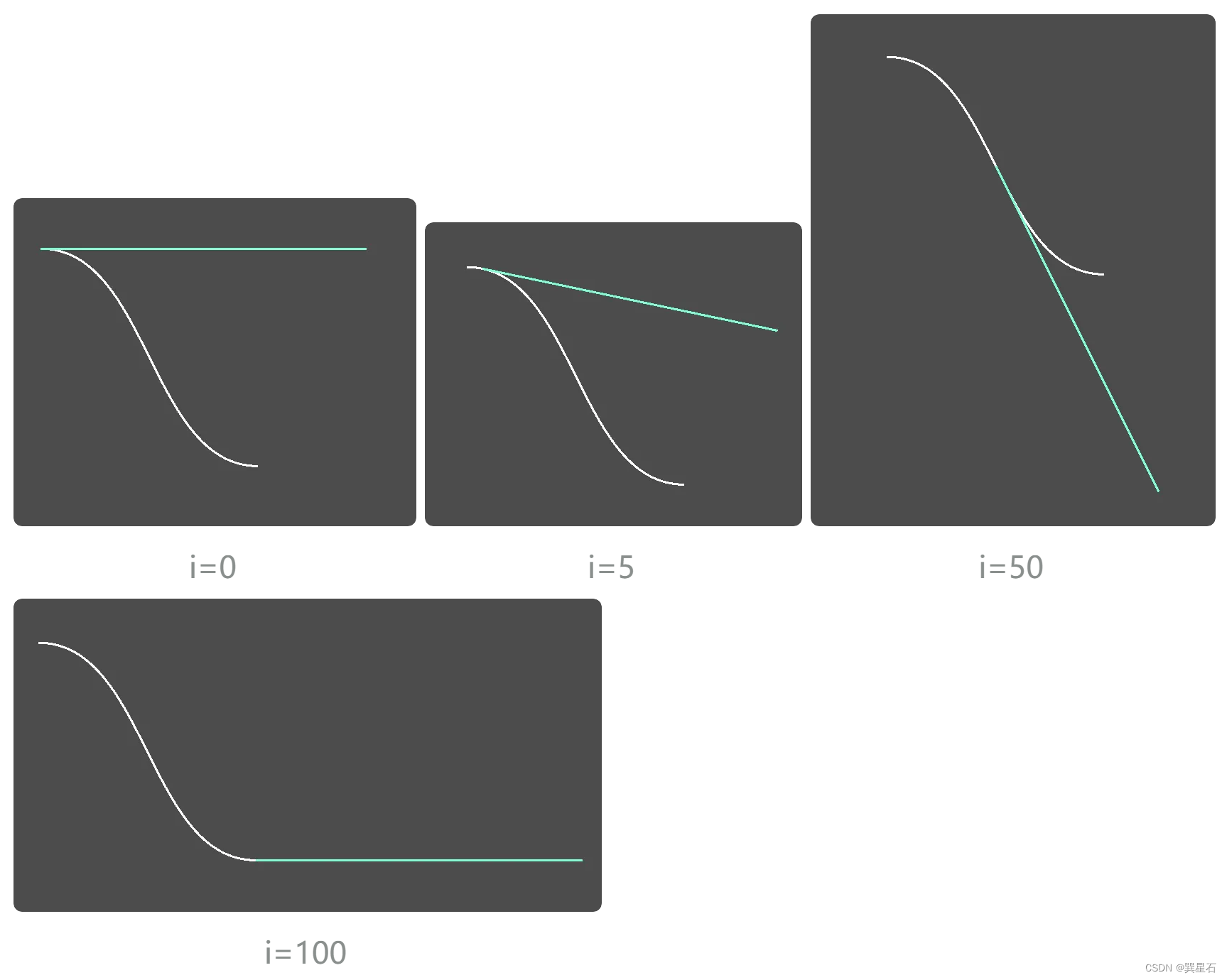
其中i是指曲線上點的索引,不同的i可以從points[i]中獲取代表在i/float(steps)處的點。
以下是一些i值下對應點與“導數”點連線的情況:
將極坐標點函數運用于貝塞爾控制點
# 極坐標點函數 - 通過角度和長度定義一個點
func pVector2(angle:float = 0.0,length:float =0.0) -> Vector2:var dir = Vector2.RIGHT.rotated(deg_to_rad(angle))return dir * length
Vector2很難直觀的表達方向和距離信息,pVector2則可以,所以在設定貝塞爾控制點時,可以使用極坐標點函數。
extends Node2Dvar p1 = Vector2(100,100) # 起點
var p2 = Vector2(200,200) # 終點
var ctl_1 = pVector2(0,50) # 控制點1
var ctl_2 = pVector2(180,50) # 控制點2var points:PackedVector2Array = [] # 曲線點集合
var steps = 100; # 點的數目,越多曲線越平滑var curve_color:= Color.WHITE # 曲線繪制顏色
var ctl_color:= Color.AQUAMARINE # 控制點和連線繪制顏色func _ready() -> void:# 求曲線點集for i in range(steps+1):var p = p1.bezier_interpolate(p1+ctl_1,p2+ctl_2,p2,i/float(steps))points.append(p)func _draw() -> void:# 繪制控制點draw_arc(p1+ctl_1,2,0,TAU,10,ctl_color,1)draw_arc(p2+ctl_2,2,0,TAU,10,ctl_color,1)# 繪制曲線端點與控制點的連線draw_line(p1,p1+ctl_1-Vector2(1,0),ctl_color,1)draw_line(p2,p2-ctl_1+Vector2(1,0),ctl_color,1)# 繪制貝塞爾曲線draw_polyline(points,curve_color,1)
繪制效果如下:
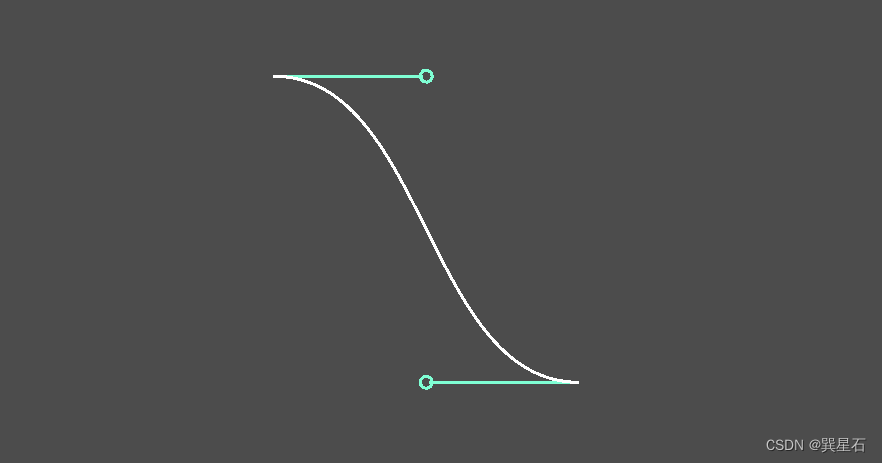
可以看到,我們可以更直觀的設定控制點在起點或終點的哪個方向,以及多長。
貝塞爾曲線函數
我們可以將貝塞爾曲線上點的求取過程封裝為一個函數,這樣就可以直接調用。
# 求兩點之間的貝塞爾曲線
func bezier_curve(p1:Vector2,p2:Vector2,ctl_1:=Vector2(),ctl_2:=Vector2(),points_count:=10) -> PackedVector2Array:var points:PackedVector2Array = []# 求曲線點集for i in range(points_count+1):var p = p1.bezier_interpolate(p1+ctl_1,p2+ctl_2,p2,i/float(points_count))points.append(p)return points
同樣我們可以編寫一個貝塞爾曲線繪制函數,用來直接在CanvasItem上調用和繪制:
# 繪制貝塞爾曲線
func draw_bezier_curve(canvas:CanvasItem,p1:Vector2,p2:Vector2,ctl_1:=Vector2(),ctl_2:=Vector2(),points_count:=10):var points:PackedVector2Array = [] # 曲線點集合points.append_array(bezier_curve(p1,p2,ctl_1,ctl_2,points_count))# 繪制控制點draw_arc(p1+ctl_1,2,0,TAU,10,ctl_color,1)draw_arc(p2+ctl_2,2,0,TAU,10,ctl_color,1)# 繪制曲線端點與控制點的連線draw_line(p1,p1+ctl_1-Vector2(1,0),ctl_color,1)draw_line(p2,p2+ctl_2-Vector2(1,0),ctl_color,1)# 繪制貝塞爾曲線draw_polyline(points,curve_color,1)
測試代碼:
extends Node2Dvar p1 = Vector2(100,100) # 點1
var p2 = Vector2(200,200) # 點2
var p3 = Vector2(400,300) # 點3
var ctl_1 = pVector2(-90,100) # 控制點1
var ctl_2 = pVector2(-45,100) # 控制點2
var ctl_3 = pVector2(135,100) # 控制點3
var ctl_4 = pVector2(45,100) # 控制點4var steps = 100; # 點的數目,越多曲線越平滑var curve_color:= Color.WHITE # 曲線繪制顏色
var ctl_color:= Color.AQUAMARINE # 控制點和連線繪制顏色func _draw() -> void:draw_bezier_curve(self,p1,p2,ctl_1,ctl_2,50)draw_bezier_curve(self,p2,p3,ctl_3,ctl_4,50)

可以看到:
- 通過給定連續的點和控制點,可以創建連續的貝塞爾曲線
- 在連接處,通過使用完全反向的控制點,可以讓貝塞爾曲線連接處更絲滑
多點連續貝塞爾曲線繪制函數
通過以PackedVector2Array形式傳入多個關鍵點和控制點,我們便可以更輕松的繪制多點連續貝塞爾曲線。
函數如下:
# 繪制由多個點和控制點順序組成的貝塞爾曲線
func draw_points_bezier_curve(canvas:CanvasItem,points:PackedVector2Array,ctls:PackedVector2Array,points_count:=10):# 求所有點之間的貝塞爾曲線點for i in range(points.size() -1):var seg = [points[i],points[i+1]] # 線段var ctl = [ctls[i * 2],ctls[i * 2 + 1]] # 控制點draw_bezier_curve(canvas,seg[0],seg[1],ctl[0],ctl[1],points_count)
測試代碼:
extends Node2D# 曲線關鍵點
var points:PackedVector2Array = [Vector2(100,100),Vector2(200,200),Vector2(400,300)
]
# 控制點
var ctls:PackedVector2Array = [pVector2(-90,100),pVector2(-45,100),pVector2(135,100),pVector2(45,100)
]var curve_color:= Color.WHITE # 曲線繪制顏色
var ctl_color:= Color.AQUAMARINE # 控制點和連線繪制顏色func _draw() -> void:draw_points_bezier_curve(self,points,ctls,50)
繪制效果:

繪制心形曲線
通過利用上面的多點連續貝塞爾曲線繪制函數,我們便可以通過一系列頂點和控制點數據,繪制處一個簡單的心形曲線。
extends Node2D# 曲線關鍵點
var points:PackedVector2Array = [Vector2(100,100),Vector2(100,200),Vector2(100,100),
]
# 控制點
var ctls:PackedVector2Array = [pVector2(-38,120),pVector2(-25,100),pVector2(-155,100),pVector2(-142,120),
]
繪制效果:

基于貝塞爾曲線的特殊圖形參數化函數
一些復雜但常見的圖形比如心形等,起始可以用幾個坐標點和控制點數據描述和復現。
因此完全可以基于基礎的圖形繪制函數結合貝塞爾曲線,來生成復雜的圖形。
甚至可以編寫相應的函數來快速生成某種圖形。


)
















