繪制一維正態分布代碼

% 給定的均值和標準差  
mu = 0; % 例如，你可以改變這個值  
sigma = 1; % 例如，你可以改變這個值  % 定義x的范圍（例如，從mu-3*sigma到mu+3*sigma，步長為0.1）  
x = mu - 3*sigma:0.1:mu + 3*sigma;  % 計算正態分布的PDF值  
y = normpdf(x, mu, sigma);  % 繪制圖形  
figure; % 創建一個新的圖形窗口  
plot(x, y, 'LineWidth', 2); % 繪制PDF圖像  
grid on; % 添加網格線  
xlabel('x'); % x軸標簽  
ylabel('f(x)'); % y軸標簽  
title(['服從X~N(', num2str(mu), ',', num2str(sigma), ')的正態分布']); % 標題，包含mu和sigma值  % 如果需要，可以添加正態分布曲線下的陰影部分來表示概率  
hold on; % 保持當前圖形  
fill([x(1), x, x(end)], [0, y, 0], 'r'); % 填充陰影部分  
hold off; % 釋放圖形

計算二維正態分布聯合概率密度

二維正態分布的概率密度函數（PDF）可以用兩個一維正態分布的隨機變量 $X$ 和 $Y$ 的均值 ${\mu }_X,{\mu }_Y$，標準差 ${\sigma }_X,{\sigma }_Y$，以及它們之間的相關系數 $\rho$ 來表示。相關系數 $\rho$ 是協方差 $\text{Cov}(X,Y)$ 和兩個隨機變量標準差的乘積的比值，即 $\rho =\frac{\text{Cov}(X,Y)}{{\sigma }_X{\sigma }_Y}$，其值范圍在 $[?1,1]$ 之間。

對于二維正態分布，其聯合概率密度函數 $f(x,y)$ 可以寫作：

$$f(x,y)=\frac{1}{2\pi {\sigma }_X{\sigma }_Y\sqrt{1?{\rho }^2}}\exp \left(?\frac{1}{2(1?{\rho }^2)}\left[{\left(\frac{x?{\mu }_X}{{\sigma }_X}\right)}^2?2\rho \left(\frac{x?{\mu }_X}{{\sigma }_X}\right)\left(\frac{y?{\mu }_Y}{{\sigma }_Y}\right)+{\left(\frac{y?{\mu }_Y}{{\sigma }_Y}\right)}^2\right]\right)$$

這里，$\exp$ 表示自然指數函數。這個公式體現了 $X$ 和 $Y$ 之間的線性關系強度和方向，由相關系數 $\rho$ 控制。當 $\rho =0$ 時，$X$ 和 $Y$ 是獨立的，其聯合分布可以分解為各自邊際分布的乘積；當 $\rho =1$ 或 $\rho =?1$ 時，表明 $X$ 和 $Y$ 完全正相關或完全負相關，即一個變量的增加（減少）總是伴隨著另一個變量按確定比例的增加（減少）。通過調整 $\rho$，可以在保持各自分布形態不變的情況下，描述兩個隨機變量之間不同的依賴關系。
繪制二維正態分布代碼如下

% 定義二維正態分布的均值向量和協方差矩陣  
mu = [0 0]; % 均值向量  
Sigma = [1 0.5; 0.5 2]; % 協方差矩陣  % 定義x和y的范圍和步長  
[x, y] = meshgrid(-5:0.1:5, -5:0.1:5); % 創建一個網格  % 使用mvnpdf函數計算二維正態分布的PDF值  
z = mvnpdf([x(:) y(:)], mu, Sigma);  % 將z重新塑形為與x和y相同的維度  
z = reshape(z, size(x));  % 使用surf函數繪制三維圖像  
figure;  
surf(x, y, z);  
xlabel('X');  
ylabel('Y');  
zlabel('Probability Density');  
title('Two-dimensional Normal Distribution');  % 使用contour函數繪制等高線圖  
figure;  
contour(x, y, z);  
xlabel('X');  
ylabel('Y');  
title('Contour Plot of Two-dimensional Normal Distribution');

這里的協方差矩陣為
$$\left(\begin{array}{cc}{\sigma }_X^2& \rho {\sigma }_X{\sigma }_Y\\ \rho {\sigma }_X{\sigma }_Y& {\sigma }_Y^2\end{array}\right)$$
效果如下

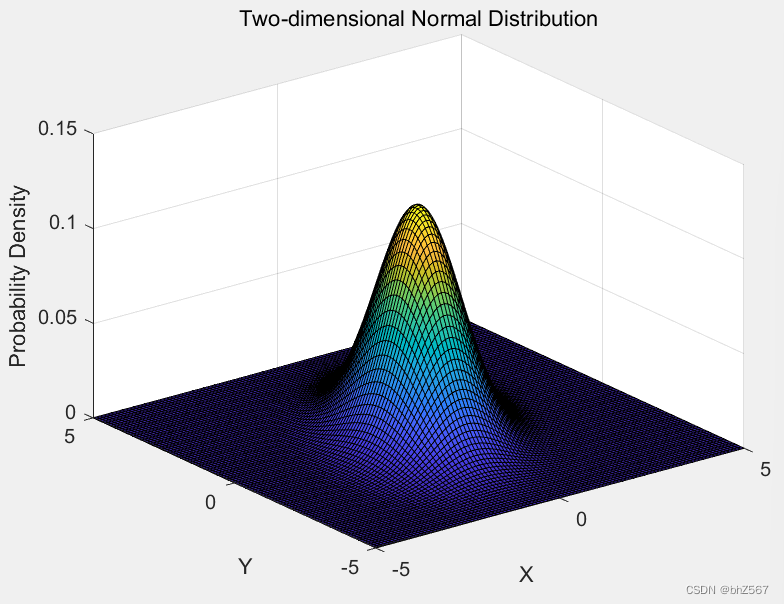
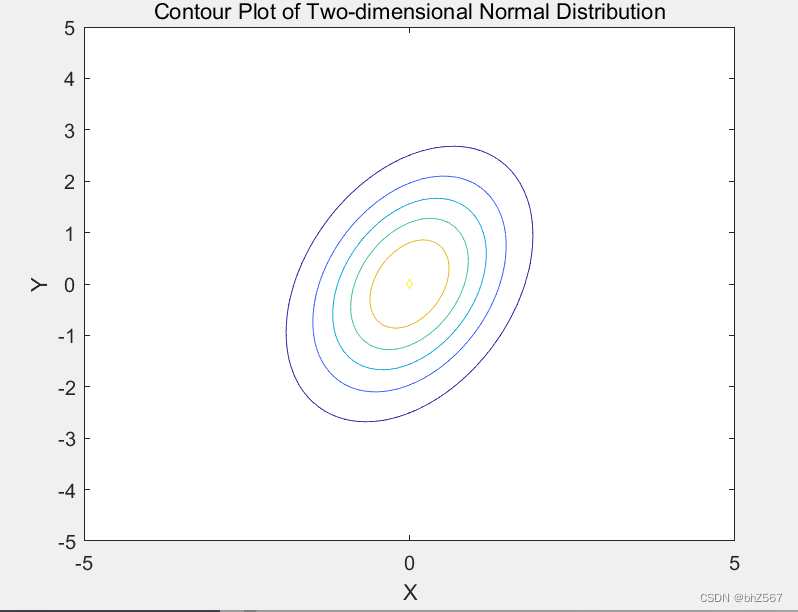
若要算某一點的概率密度，代碼如下

% 給定參數
mu_X = 0; mu_Y = 0; sigma_X = 1; sigma_Y = 1; rho = 0.5;
x = 1; y = 1;% 計算概率密度
pdf_value = bivariateNormalPDF(x, y, mu_X, mu_Y, sigma_X, sigma_Y, rho);fprintf('在點 (%.2f, %.2f) 處的概率密度為: %.4f\n', x, y, pdf_value);
function pdf_val = bivariateNormalPDF(x, y, mu_X, mu_Y, sigma_X, sigma_Y, rho)% 計算標準化變量z_X = (x - mu_X) / sigma_X;z_Y = (y - mu_Y) / sigma_Y;% 計算概率密度函數的值exponent = -(1/(2*(1-rho^2))) * (z_X^2 - 2*rho*z_X*z_Y + z_Y^2);normalization_constant = 1 / (2*pi*sigma_X*sigma_Y*sqrt(1-rho^2));pdf_val = normalization_constant * exp(exponent);
end

本文采用AI輔助創作