1.7 訓練一個神經網絡

?????? 對于訓練神經網絡，有兩個步驟，即前向傳遞和誤差反向傳播。

1.7.1 前向傳播和反向傳播

?????? 在前向傳遞中，輸入被饋送到模型并與權重向量相乘，并為每一層添加偏差以計算模型的輸出。密集層或全連接層第l層的輸入、 激活函數和輸出表示如下：

（1.57）

?????? 其中N表示第l層的神經元數量，是第l層任務需要學習的權重，σ()是激活函數

?????? 反向傳播如下所述。考慮一個樣本，其輸入和預期輸出和實際輸出，因此一個樣本的誤差為?，其中是權重的函數。使用梯度下降算法更新權重以最小化誤差，可以表示如下：

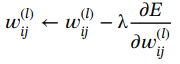(1.58)

?????? 在式(1.58)，可計算如下：

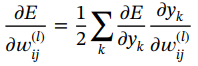(1.59)

?????? 其中，。

?????? 由于是的函數，因此可以推導出

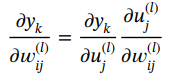(1.60)

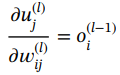(1.61)

?????? 這是在前饋步驟中計算的。

?????? 因此，把它們放在一起給了我們:

(1.62)

?????? 神經網絡訓練過程中的一些重要方面如下：

?????? 1.學習率：每次權重更新都由參數 λ 控制，稱為學習率參數。如果學習率太小，那么可能會導致學習速度非常慢，很容易被困在局部最小值中，并且可以持續運行多次迭代。另一方面，如果學習率很大，那么它可能會越過最小值，可能無法收斂，并可能發散。因此，根據架構、數據集、傳遞函數等選擇良好的學習率非常重要。圖1.18說明了選擇小學習率和大學習率對梯度下降的影響。

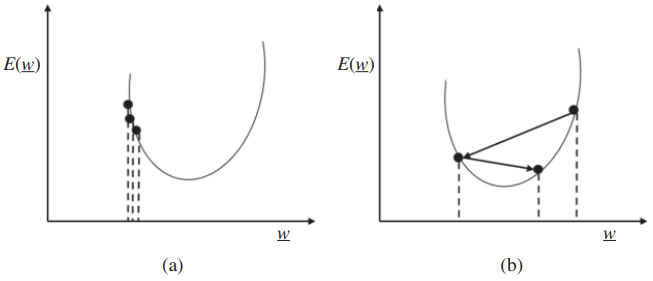
圖1.18 (a)學習率小和(b)學習率大時梯度下降的圖示。

?????? 2. 權重初始化：在初始化過程中隨機化權重很重要;否則，權重的對稱性會阻止網絡學習。通常，使用小的隨機值，這在層中的神經元數量增長時非常重要，因為加權和可能會使優化函數飽和。

?????? 3. 過擬合和欠擬合：在機器學習中，目標不僅是最小化樣本內數據（即可用或可見的數據）的成本函數，而且還要對樣本外數據（即訓練期間不可用或不可見的數據）進行泛化。在訓練過程中，可用的數據集分為訓練集、驗證集和測試集。訓練數據集用于訓練模型，驗證數據集用于設置模型的超參數，測試數據集用于估計樣本外或泛化精度。

?????? 當訓練數據的性能較差時，可以將其視為欠擬合，通常是由于學習率選擇不當或神經網絡維度不足。此錯誤稱為“偏差”。圖1.19的左列說明了欠擬合問題。當訓練數據的性能良好（即近似精度好），但測試或驗證數據性能差（即泛化精度差）時，就會出現過擬合問題。這種現象也稱為“方差”，如圖1.19的右欄所示。如果訓練集大小不足或模型復雜度對于數據來說太高，則模型可以很好地記住或近似訓練數據，但不能很好地泛化測試數據，即過度擬合。訓練機器學習模型的目的是找到一個如圖 1.19 中間列所示的模型，其中訓練誤差（偏差）和泛化誤差（方差）最小化。通常，訓練會找到一個模型，以便在偏差和方差之間實現平衡，通常被稱為“偏差-方差”權衡。在深度學習的情況下，“偏差-方差”權衡不適用，因為有單獨的機制來減少偏差和方差，因此權衡不容易適用。

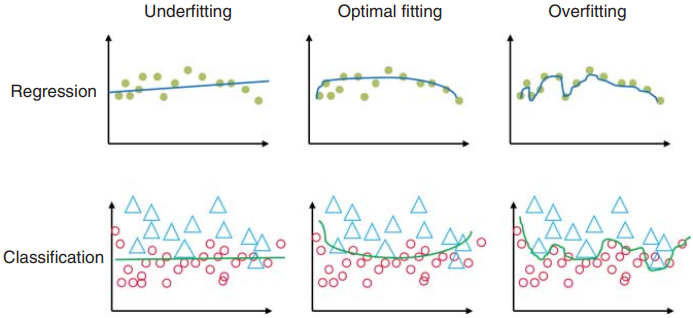
圖1.19 模型欠擬合和過擬合的圖示。

?????? 4. 維度的詛咒：機器學習的另一個關鍵方面是維度的詛咒。維度的詛咒與過擬合密切相關。在高維空間中，大多數訓練數據都位于定義特征空間的超立方體的角落。特征空間角落中的實例比超活躍球體質心周圍的實例更難分類。因此，隨著特征或維度數量的增加，我們需要準確泛化的數據量也呈指數級增長。

1.7.2 優化器

?????? 優化器是幫助改變模型的權重和偏差的方法，以便將損失函數最小化。對標準隨機梯度下降 （SGD） 算法提出了一些修改，即，其中)、?分別表示損失函數及其導數。和表示更新步驟后和之前的權重，λ表示學習率。以下是改進標準 SGD 的優化器列表：

?????? 1. 動量：它加速SGD朝向相關方向，同時減少振蕩。它基本上是將先前權重更新的一部分添加到當前更新向量中，從而確保在一定程度上保留先前更新的方向，同時使用當前更新梯度來微調最終更新方向。動量引入了另一個變量，可以表示如下

(1.63)

?????? 2. Nesterov 加速梯度 [45]：雖然動量有助于降低噪聲并加速收斂，但它也會引入誤差。在Nesterov加速梯度中，通過將先前的權重更新的一部分包含在當前更新向量中以執行權重更新來解決此問題，其表示如下：

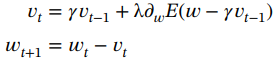(1.64)

?????? γ的典型值 = 0.9。

?????? 3. Adagrad [46]：Adagrad 的動機是每個參數都有一個自適應學習率;然而，早期的方法具有固定的學習率。Adagrad 確保依賴于迭代的隱藏層的不同神經元具有不同的學習率。其背后的直覺是，對于不頻繁的參數，應該進行較大的更新，而對于頻繁的參數，應該進行較小的更新。對于每次權重更新，學習率調整如下：

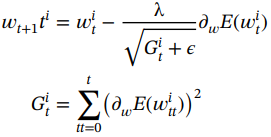(1.65)

?????? 由于梯度的平方和不斷增長，因此自適應地會導致較小的學習率。參數ε有助于避免除以零的問題。

?????? 4. RMSprop [47]：Adagrad 的一個問題是，在DNN中經過幾次迭代后，學習速率變得非常小，從而導致死神經元問題，并導致這些神經元沒有更新。RMSprop 修復了此問題，即使在多次參數更新后，學習也可以繼續。在RMSprop 中，學習率是梯度的指數平均值，而不是像 Adagrad 中那樣的梯度平方和的累積和。通過將梯度累積限制在某個過去來計算每個權重的平方梯度的移動平均值，可以表示如下：

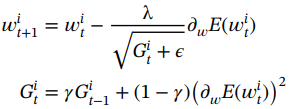?(1.66)

?????? 5. Adadelta [48]：Adadelta 是對 Adagrad 的另一項改進，可在多次參數更新后繼續學習。但 Adadelta 的計算成本很高。在這里，梯度累積僅限于某個過去的更新，方法是計算每個權重參數的平方梯度和參數更新的移動平均值，如下所示：

(1.67)

?????? 6. 自適應矩估計(ADAM)[49]：Adam 優化器是當今最流行和使用最廣泛的優化器之一。它既存儲類似于動量的過去梯度的衰減平均值，也存儲過去平方梯度的衰減平均值，類似于 RMSprop和Adadelta。ADAM可以表示為以下等式，其中動量通過使用第一和第二矩添加到RMSprop中，即梯度的平均值和方差：

(1.68)

?????? 其中β1和β2是梯度均值和方差的移動平均實現中的遺忘因子。Adam易于實現且計算效率高，并且由于移動平均實現，需要的內存更少。

1.7.3 損失函數

?????? 神經網絡被表述為一個優化問題。候選解，即網絡的權重，應最小化或最大化給定目標函數的分數。

?????? 在回歸問題的情況下，目標是預測一個實值量。在這種情況下，在輸出層使用線性激活單元，并使用 MSE 作為損失函數。回歸的均方損失如下：

(1.69)

?????? 其中y和?分別是神經網絡的真實值和預測值。

?????? 對于分類問題建模，其思路是將輸入變量映射到類標簽，這意味著目標是預測示例屬于特定類的概率。在最大似然估計下，網絡的訓練試圖找到一組模型權重，以最小化模型給定數據集的預測概率分布與訓練數據集中概率分布之間的差異。這稱為CE損失，在二元分類的情況下，在輸出端配置為sigmoid激活，而對于多類分類，在輸出端使用 softmax 激活。在這兩種情況下，問題都表述為預測屬于特定類的給定輸入的最大可能性。

?????? 二元分類的二元CE損失如下：

(1.70)

?????? 其中p是類1的概率，1?p 是類0的概率，?是神經網絡的預測概率。