目錄

1.二叉搜索樹的結構與特性

2.二叉搜索樹的實現

（1）節點

（2）功能實現

插入：

刪除：

查找:

打印：

3.測試

插入刪除：

查找：

4.變種測試，即帶value值

單詞查找：

個數統計：

---

1.二叉搜索樹的結構與特性

BSTree（二叉搜索樹）是一個神奇的數據結構，其的特點是，左子樹的所有值比根小，而右子樹的所有值比根大

根據這種特性，我們可以從該結構中快速的搜索一個數的存在，速度則為樹的高度次。

類似于這樣的數。

2.二叉搜索樹的實現

（1）節點

因為是樹的結構，所以肯定少不了節點：

    template<class K>struct BSTreeNode{BSTreeNode<K>* _left;BSTreeNode<K>* _right;K _key;BSTreeNode(const K& key):_left(nullptr), _right(nullptr), _key(key){}};

利用初始化列表將其進行初始化。

（2）功能實現

該結構應該有插入、刪除功能，因為叫搜索樹，所有肯定有查找功能

插入：

    bool Insert(const K& key){if (_root == nullptr){_root = new Node(key);return true;}Node* parent = nullptr;Node* cur = _root;while (cur){if (key < cur->_key){parent = cur;cur = cur->_left; }else if (key > cur->_key){parent = cur;cur = cur->_right;}else{return false;}}cur = new Node(key);if (parent->_key > key)parent->_left = cur;elseparent->_right = cur;return true;}

插入功能的實現邏輯很簡單，只需要遵循根比左子樹大，比右子樹小即可。

刪除：

bool Erase(const K& key){Node* cur = _root;Node* parent = cur;while (cur){if (key < cur->_key){parent = cur;cur = cur->_left;}else if (key > cur->_key){parent = cur;cur = cur->_right;}else{if (cur->_left == nullptr){if (parent == cur)_root = cur->_right;else{if (parent->_left == cur){parent->_left = cur->_right;}else{parent->_right = cur->_right;}}}else if(cur->_right == nullptr){if (parent == cur)_root = cur->_left;else{if (parent->_left == cur){parent->_left = cur->_left;}else{parent->_right = cur->_left;}}}else{Node* MinRight = cur->_left; parent = cur;while (MinRight->_right){parent = MinRight;MinRight = MinRight->_right;}cur->_key = MinRight->_key;if(parent->_right == MinRight)parent->_right = MinRight->_left;elseparent->_left = MinRight->_left;}return true;}}return false;}

刪除功能的邏輯就比較復雜了，分三種情況討論，一種是cur有兩個子節點，二是cur有一個子節點，三是cur無子節點。

最后可以將二、三中情況合并處理，因為都存在nullptr。

查找:

    bool find(const K& key){Node* cur = _root;while (cur){if (key < cur->_key){cur = cur->_left;}else if (key > cur->_key){cur = cur->_right;}else{return true;}}return false;}

查找邏輯簡單，無須多說，只需根據二叉搜索樹的特性畫圖即可。

同時加入一個打印功能方便觀察：

打印：

        void Inorder(){_Inorder(_root);cout << endl;}void _Inorder(Node* _root){if (_root == nullptr){return;}_Inorder(_root->_left);cout << _root->_key << ' ';_Inorder(_root->_right);}

創建一個_Inorder的原因是方便讀取底層的_root元素，然后中序遍歷即可

3.測試

插入刪除：

查找：

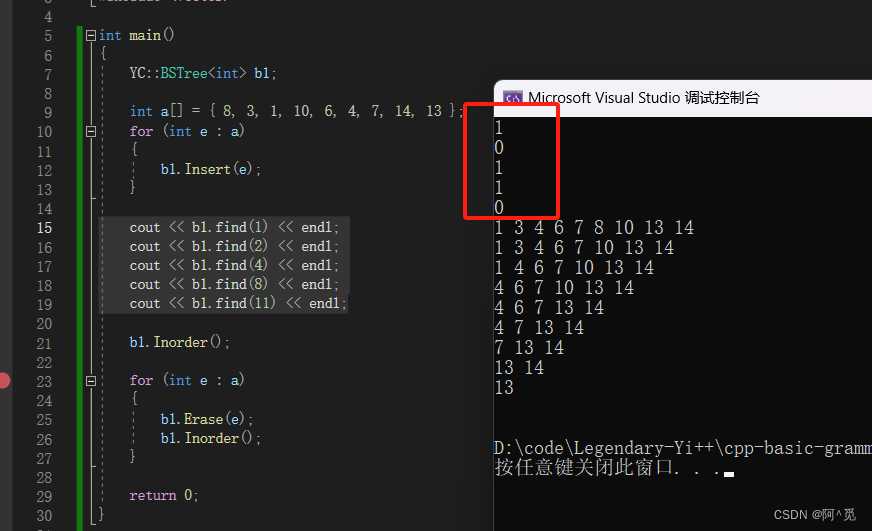
1表示存在，0表示不存在

4.變種測試，即帶value值

namespace YC_Value
{template<class K, class V>struct BSTreeNode{BSTreeNode<K, V>* _left;BSTreeNode<K, V>* _right;K _key;V _value;BSTreeNode(const K& key, const V& value):_left(nullptr), _right(nullptr), _key(key), _value(value){}};template<class K, class V>class BSTree{typedef BSTreeNode<K, V> Node;public:bool Insert(const K& key, const V& value){if (_root == nullptr){_root = new Node(key, value);return true;}Node* parent = nullptr;Node* cur = _root;while (cur){if (key < cur->_key){parent = cur;cur = cur->_left;}else if (key > cur->_key){parent = cur;cur = cur->_right;}else{return false;}}cur = new Node(key, value);if (parent->_key > key)parent->_left = cur;elseparent->_right = cur;return true;}Node* find(const K& key){Node* cur = _root;while (cur){if (key < cur->_key){cur = cur->_left;}else if (key > cur->_key){cur = cur->_right;}else{return cur;}}return cur;}void Inorder(){_Inorder(_root);cout << endl;}bool Erase(const K& key){Node* cur = _root;Node* parent = cur;while (cur){if (key < cur->_key){parent = cur;cur = cur->_left;}else if (key > cur->_key){parent = cur;cur = cur->_right;}else{if (cur->_left == nullptr){if (parent == cur)_root = cur->_right;else{if (parent->_left == cur){parent->_left = cur->_right;}else{parent->_right = cur->_right;}}}else if (cur->_right == nullptr){if (parent == cur)_root = cur->_left;else{if (parent->_left == cur){parent->_left = cur->_left;}else{parent->_right = cur->_left;}}}else{Node* MinRight = cur->_left;parent = cur;while (MinRight->_right){parent = MinRight;MinRight = MinRight->_right;}cur->_key = MinRight->_key;if (parent->_right == MinRight)parent->_right = MinRight->_left;elseparent->_left = MinRight->_left;}return true;}}return false;}private:void _Inorder(Node* root){if (root == nullptr){return;}_Inorder(root->_left);cout << root->_key << ":" << root->_value << endl;_Inorder(root->_right);}private:Node* _root = nullptr;};void TestBSTree2(){BSTree<string, string> dict;dict.Insert("string", "字符串");dict.Insert("left", "左邊");dict.Insert("insert", "插入");//...string str;while (cin >> str){BSTreeNode<string, string>* ret = dict.find(str);if (ret){cout << ret->_value << endl;}else{cout << "無此單詞，請重新輸入" << endl;}}}void TestBSTree3(){// 統計次數string arr[] = { "蘋果", "西瓜", "蘋果", "西瓜", "蘋果", "蘋果", "西瓜",
"蘋果", "香蕉", "蘋果", "香蕉","蘋果","草莓", "蘋果","草莓" };BSTree<string, int> countTree;for (const auto& str : arr){auto ret = countTree.find(str);if (ret == nullptr){countTree.Insert(str, 1);}else{ret->_value++;}}countTree.Inorder();}
};

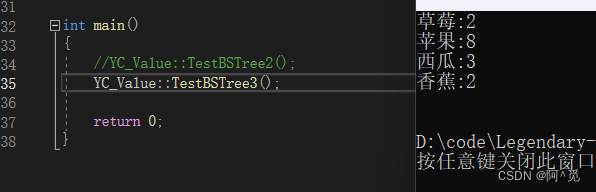
單詞查找：

個數統計：