架構設計的復雜度來源其實就是架構設計要解決的問題，主要有如下幾個：高性能、高可用、可擴展、低成本、安全、規模。復雜度的關鍵，就是新舊技術之間不是完全的替代關系，有交叉，有各自的特點，所以才需要具體問題具體分析，基于各方考慮設計合適的架構，存在合適的架構，不存在最好的架構。這篇主要討論可擴展性問題

復雜度來源

可擴展性是指，系統為了應對將來需求變化而提供的一種擴展能力，當有新的需求出現時，系統不需要或者僅需要少量修改就可以支持，無須整個系統重構或者重建

在軟件設計領域，面向對象思想、設計模式主要被用于解決可擴展性問題。設計具備良好可擴展性的系統，有兩個基本條件：正確預測變化、完美應對變化

預測變化

軟件系統在發布后，還可以不斷地修改和演進。這就意味著不斷有新的需求需要實現。如果新需求能夠少改代碼甚至不改代碼就可以實現。綜合分析，預測變化的復雜性在于：

1. 不能每個設計點都考慮可擴展性。如果每個點都考慮可擴展性，架構師會不堪重負，架構設計也會異常龐大且最終無法落地
2. 不能完全不考慮可擴展性。不能完全不做預測，否則可能系統剛上線，馬上來新的需求就需要重構，這同樣意味著前期很多投入的工作量也白費了
3. 所有的預測都存在出錯的可能性。如果預測的事情出錯，我們期望中的需求遲遲不來，甚至被明確否定，那么基于預測做的架構設計就沒什么作用，投入的工作量也就白費了

針對上邊這些復雜性，有個經驗性的原則：只預測 2 年內的可能變化，不要試圖預測 5 年甚至 10 年后的變化, 變化快的行業，能夠預測 2 年已經足夠了；而變化慢的行業，本身就變化慢，預測本身的意義不大，預測 5 年和預測 2 年的結果是差不多的。所以2 年法則在大部分場景下都是適用的

應對變化

即使預測的比較準了，但是系統設計的時候如何應對變化的擴展性也不是一個簡單的問題，應對變化有兩個方案：

1 提煉出變化層和穩定層

這種方案是：將不變的部分封裝在一個獨立的穩定層，將變化封裝在一個變化層（也叫適配層）。這種方案的核心思想是通過變化層來隔離變化

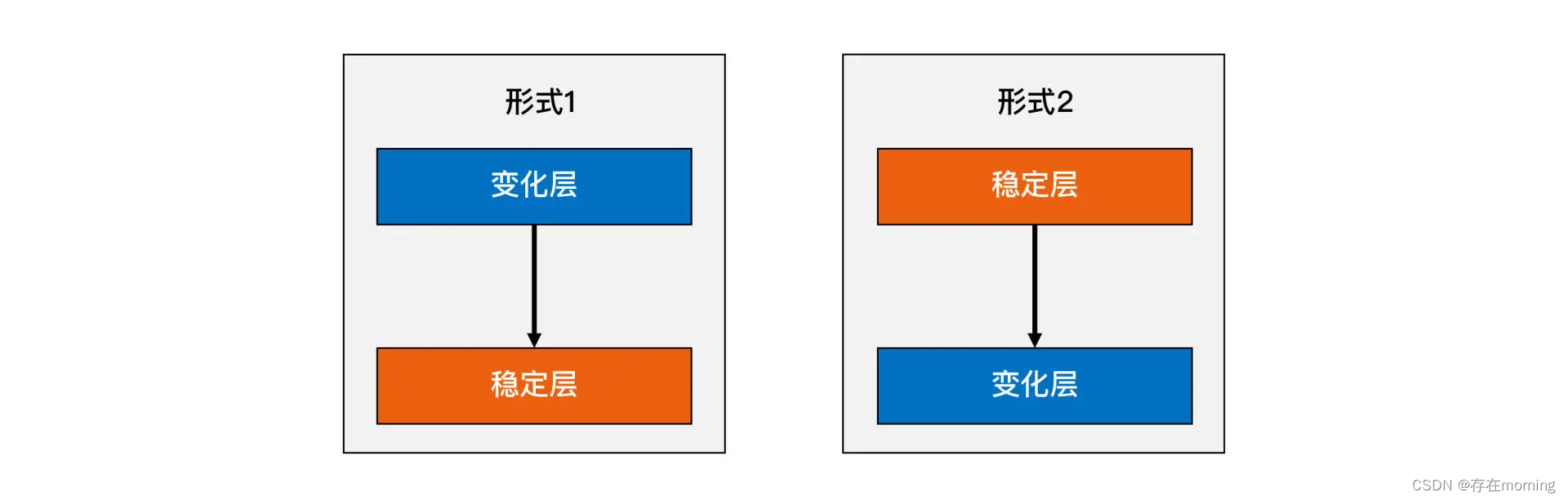
無論是變化層依賴穩定層，還是穩定層依賴變化層都是可以的，需要根據具體業務情況來設計。如果系統需要支持 XML、JSON、ProtocolBuffer 三種接入方式，那么最終的架構就是“形式 1”架構；如果系統需要支持 MySQL、Oracle、DB2 數據庫存儲，那么最終的架構就變成了“形式 2”的架構了

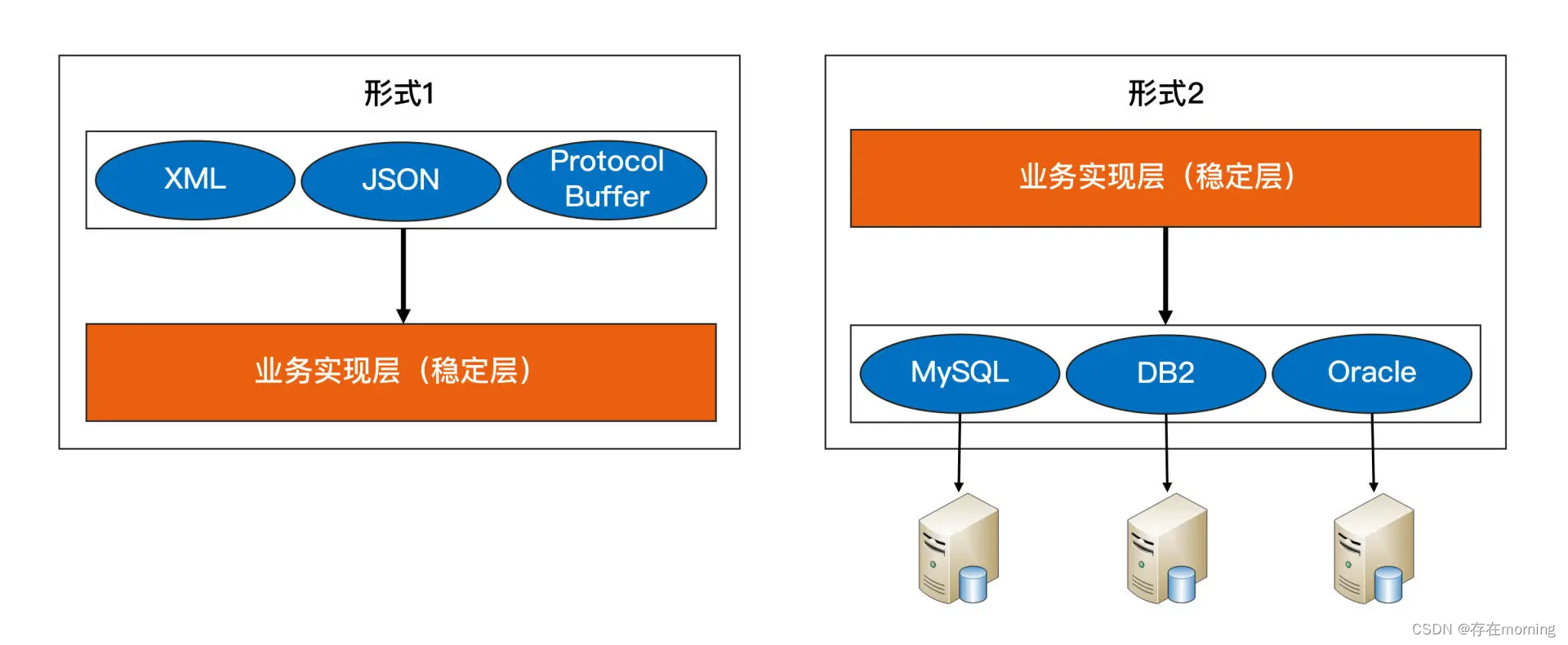
這種方案的復雜度在于分層的拆分依據，以及各層的接口如何設計

1. 明確變化層和穩定層如何拆分：對于哪些屬于變化層，哪些屬于穩定層需要明確
2. 變化層和穩定層之間的接口如何設計：對于穩定層來說，接口肯定是越穩定越好；但對于變化層來說，在有差異的多個實現方式中找出共同點，并且還要保證當加入新的功能時，原有的接口不需要太大修改

3 提煉出抽象層和實現層

提煉出一個“抽象層”和一個“實現層”，因為抽象層的接口是穩定的不變的，我們可以基于抽象層的接口來實現統一的處理規則，而實現層可以根據具體業務需求定制開發不同的實現細節，所以當加入新的功能時，只要遵循處理規則然后修改實現層，增加新的實現細節就可以了，無須修改抽象層。典型的實踐就是設計模式和規則引擎。

1 寫 2 抄 3 重構原則

不要一開始就考慮復雜的可擴展性應對方法，而是等到第三次遇到類似的實現的時候再來重構，重構的時候采取隔離或者封裝的方案

• 1 寫：最開始三方支付選擇了微信錢包對接，此時不需要考慮太多可擴展性，直接快速對照微信支付的 API 對接即可，因為業務是否能做起來還不確定。
• 2 抄：后來發現業務發展不錯，決定要接入支付寶，此時還是可以不考慮可擴展，直接把原來微信支付接入的代碼拷貝過來，然后對照支付寶的 API，快速修改上線。
• 3 重構：因為業務發展不錯，為了方便更多用戶，決定接入銀聯云閃付，此時就需要考慮重構，參考設計模式的模板方法和策略模式將支付對接的功能進行封裝。

開始可以寫一些if語句進行分支判斷，后續場景多起來后可以考慮設計模式去實現。

總結一下

結合這篇Blog，其實我感覺主要是如何在過度設計與不可擴展間去權衡。長期預測的代價和變數太多，可能在落地前業務就涼了，不做預測又可能剛開始迭代就發現難以支持。所以2年預測是一個經驗值，如果到了2年業務發展的好了，會倒逼決策層給資源給錢進行架構升級，如果都用不了2年就涼了那5-10年預測就沒意義了；在預測的前提下，我們在方案設計的時候是否可以考慮短、中、長三種方案，短期策略一般考慮的變化少，短視，但迅速，修改小，立竿見影。長期策略一般看重遠期，但成本高很高，也很可能預測不中。綜合成本情況下如果決定采用短期策略，要考慮如果預測的變化發生了，系統修改為長期策略的代價有多大（想在做前），如果可以演化切換那可以，如果成本很高甚至切換不到長期策略，就需要重新思考了；再說重構，重構應該是一個小步快跑的模式，不要一開始就過度抽象的設計去炫技，而是先實現最基本功能，然后逐步隨業務迭代進行變化層隔離。