AVL樹模擬

1.概念

雖然二叉搜索樹可以縮短查找的效率，但如果數據有序或者接近有序時二叉搜索樹樹將退化為單支樹，查找元素相當于在順序表中搜索元素，效率低下。AVL
樹是具有一下性質的二叉搜索樹：????????

????????1.它的左右子樹都是AVL樹

????????2.左右子樹的高度差的絕對值不超過1

如果一個二叉搜索樹是高度平衡的，它就是AVL樹。如果它有n個節點，其高度可保持在log N,搜索時間復雜度為O(log N)；

2.節點定義

template<class T>
struct AVLTreeNode
{AVLTreeNode(T key):_bf(0), _key(key){}AVLTreeNode* _left = nullptr;AVLTreeNode* _right = nullptr;AVLTreeNode* _parent = nullptr;int _bf;					//平衡因子T _key;
};

3.AVL插入

AVL樹的插入就是在二叉搜索樹的基礎上引入了平衡因子，因此AVL樹也可以看成是二叉搜索樹。

AVL樹的插入過程可以分為兩部分：

? ? ? ? 1.按照二叉搜索樹的方式插入新節點

? ? ? ? 2.調整平衡因子

3.1 按照二叉搜索樹的方式插入新的節點

bool Insert(T key)
{Node* newnode = new Node(key);if (_root == nullptr){_root = newnode;return true;}Node* cur = _root;Node* parent = nullptr;//尋找插入位置while (cur){if (key > cur->_key){parent = cur;cur = cur->_right;}else if (key < cur->_key){parent = cur;cur = cur->_left;}else return false;}//插入新的節點newnode->_parent = parent;if (key < parent->_key) parent->_left = newnode;else parent->_right = newnode;
}

3.2調整平衡因子

新節點插入后，AVL樹的平衡性可能遭到破壞，因此就需要更新平衡因子，并檢測是否破壞了AVL樹的平衡性

當newnode插入后，parent的平衡因子一點需要調整，在插入之前parent的平衡因子分為三種情況：-1，0，1。

調整方式分為以下兩種：

????????當新節點插入到parent左側時，parent平衡因子-1；

????????當新節點插入到parent右側時，parent平衡因子+1；

此時parent的平衡因子有以下三種情況：0，正負1，正負2

????????1.如果此時的平衡因子為0，說明插入新的節點后parent平衡了，滿足AVL樹的性質，無需繼續向上調整。

? ? ? ? 2.如果此時平衡因子為正負1，說明插入新的節點后parent為根的樹高度增加，需要繼續向上調整。

? ? ? ? 3.如果此時平衡因子為正負2，說明parent違反了AVL樹的性質，需要對其經行旋轉處理。

cur = newnode;
while (parent)
{//更新平衡因子if (cur == parent->_left) parent->_bf--;else parent->_bf++;//檢查平衡因子狀態if (parent->_bf == 0) break;else if (parent->_bf == 1 || parent->_bf == -1){cur = parent;parent = parent->_parent;}//不平衡，旋轉else if (parent->_bf == 2 || parent->_bf == -2){if (parent->_bf == 2){//...}else{//...}break;}else{cout << "error: _bf";break;}
}

4. AVL樹的旋轉

?上圖在插入前，AVL樹是平衡的，新節點插入到30的左子樹(注意：此處不是左孩子)中，30左子樹增加了一層，導致以60為根的二叉樹不平衡。

要讓60平衡，只能將60左子樹的高度減少一層，右子樹增加一層， ?即將左子樹往上提，這樣60轉下來，因為60比30大，只能將其放在30的右子樹，而如果30有右子樹，右子樹根的值一定大于30，小于60，只能將其放在60的左子樹，旋轉完成后，更新節點的平衡因子即可。

在旋轉過程中，有以下幾種情況需要考慮： ?1. 30節點的右孩子可能存在，也可能不存在 ?2. 60可能是根節點，也可能是子樹如果是根節點，旋轉完成后，要更新根節點如果是子樹，可能是某個節點的左子樹，也可能是右子樹

a.右單旋


void _RotateR(Node* pParent)
{// pSubL: pParent的左孩子// pSubLR: pParent左孩子的右孩子，注意：該PNode* pSubL = pParent->_pLeft;PNode* pSubLR = pSubL->_pRight;// 旋轉完成之后，30的右孩子作為雙親的左孩子pParent->_pLeft = pSubLR;// 如果30的左孩子的右孩子存在，更新親雙親if (pSubLR) pSubLR->_pParent = pParent;// 60 作為 30的右孩子// 因為60可能是棵子樹，因此在更新其雙親前必須先保存60的雙親PNode pPParent = pParent->_pParent;// 更新60的雙親pParent->_pParent = pSubL;// 更新30的雙親pSubL->_pParent = pPParent;// 如果60是根節點，根新指向根節點的指針if (NULL == pPParent){_pRoot = pSubL;pSubL->_pParent = NULL;}else{// 如果60是子樹，可能是其雙親的左子樹，也可能是右子樹if (pPParent->_pLeft == pParent)pPParent->_pLeft = pSubL;elsepPParent->_pRight = pSubL;}// 根據調整后的結構更新部分節點的平衡因子pParent->_bf = pSubL->_bf = 0;
}

b.左單旋?

具體細節與右單旋一致。

void _RotateL(Node* pParent)
{Node* RSub = pParent->_right;Node* RSubL = RSub->_left;Node* pPParent = pParent->_parent;if (RSubL) RSubL->_parent = pParent;pParent->_right = RSubL;RSub->_left = pParent;pParent->_parent = RSub;RSub->_parent = pPParent;if (pParent == _root) _root = RSub;else{if (pPParent->_left == pParent) pPParent->_left = RSub;else pPParent->_right = RSub;}//更新平衡因子RSub->_bf = pParent->_bf = 0;
}

c.先左旋在右旋

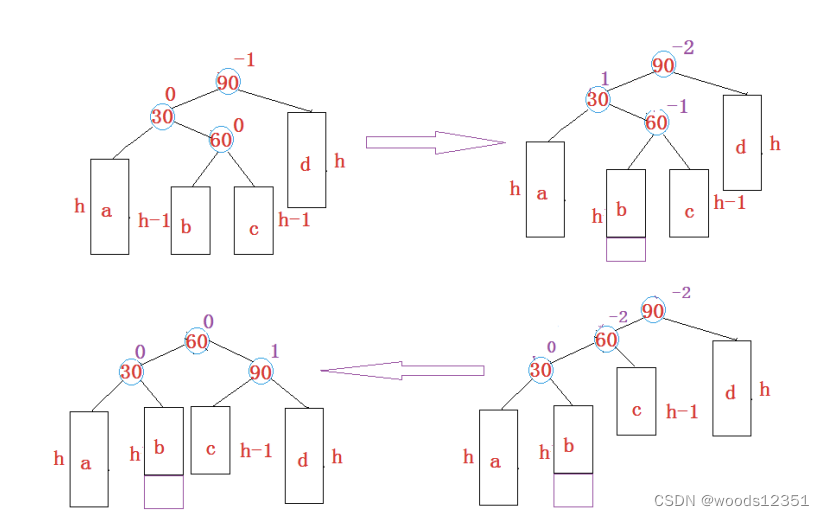
將雙旋變成單旋后再旋轉，即：先對30進行左單旋，然后再對90進行右單旋，旋轉完成后再考慮平衡因子的更新。

// 旋轉之前，60的平衡因子可能是-1/0/1，旋轉完成之后，根據情況對其他節點的平衡因子進
//行調整
void _RotateLR(PNode pParent)
{PNode pSubL = pParent->_pLeft;PNode pSubLR = pSubL->_pRight;// 旋轉之前，保存pSubLR的平衡因子，旋轉完成之后，需要根據該平衡因子來調整其他節//點的平衡因子int bf = pSubLR->_bf;// 先對30進行左單旋_RotateL(pParent->_pLeft);// 再對90進行右單旋_RotateR(pParent);if (1 == bf)pSubL->_bf = -1;else if (-1 == bf)pParent->_bf = 1;
}

d. 先右旋在左旋

void _RotateRL(Node* pParent)
{Node* RSub = pParent->_right;Node* RSubL = RSub->_left;int bf = RSubL->_bf;_RotateR(RSub);_RotateL(pParent);RSub->_bf = 0;if (bf == 1){RSub->_bf = 0;pParent->_bf = -1;}else if (bf == -1){pParent->_bf = 0;RSub->_bf = 1;}else{RSub->_bf = pParent->_bf = 0;}
}

總結：

加入以parent為根的子樹不平衡，即以parent的平衡因子為2或-2，分別考慮以下情況

? ? ? ? 1.parent的平衡因子為2，說明parent的右子樹高，設parent的右子樹的根為RSub

? ? ? ? ? ? ? ? 當RSub的平衡因子為1時，執行左單旋，

? ? ? ? ? ? ? ? 當RSub的平衡因子為-1時，執行左右雙旋。

? ? ? ? 2.parent的平衡因子為-2?，說明parent的左子樹高，設parent的左子樹的根為LSub

? ? ? ? ? ? ? ? 當LSub的平衡因子為-1時，執行右單旋。

? ? ? ? ? ? ? ? 當LSub的平衡因子為1時，執行做單旋。

當旋轉接完成后，parent為根的子樹高度已經降低，以及平衡，無需向上更新。

5.AVL樹的驗證

AVL樹實在二叉搜索樹的基礎上加了平衡性的限制，因此要驗證AVL樹可以分為兩步

? ? ? ? 1.驗證其為二叉搜索樹

? ? ? ? ? ? ? ? 如果中序遍歷結果為有序，則為二叉搜索樹

? ? ? ? 2.驗證其為平衡樹

? ? ? ? ? ? ? ? 1.每個子樹高度差的絕對值不超過1

? ? ? ? ? ? ? ? 2.節點平衡因子正確

void InOrder()
{_InOrder(_root);
}int GETHeight()
{return _GETHeight(_root);
}bool IsBalance()
{return _isBalance(_root);
}	bool _isBalance(Node* root)
{if (root->_bf >= 2 || root->_bf <= -1) return false;int HeightLeft = _GETHeight(root->_left);int HeightRight = _GETHeight(root->_right);if (abs(HeightRight - HeightLeft) > 1) return false;return _isBalance(root->_left) && _isBalance(root->_right);
}
int _GETHeight(Node* root)
{if (root == nullptr) return 0;return max(_GETHeight(root->_left), _GETHeight(root->_right)) + 1;
}
void _InOrder(Node* root)
{if (root == nullptr) return;_InOrder(root->_left);cout << root->_key << " ";_InOrder(root->_right);
}

測試代碼?

void test_AVL01()
{int a[] = { 8, 3, 1, 10, 6, 4, 7, 14, 13 };//int a[] = { 4, 2, 6, 1, 3, 5, 15, 7, 16, 14 };AVLTree<int> t1;for (auto e : a){t1.Insert(e);//cout << "Insert:" << e << "->" << t1.IsBalance() << endl;}cout << t1.GETHeight() << endl;t1.InOrder();//cout << t1.IsBalance() << endl;
}

6.AVL樹模擬代碼

#pragma oncetemplate<class T>
struct AVLTreeNode
{AVLTreeNode(T key):_bf(0), _key(key){}AVLTreeNode* _left = nullptr;AVLTreeNode* _right = nullptr;AVLTreeNode* _parent = nullptr;int _bf;					//平衡因子T _key;
};template<class T>
class AVLTree
{typedef AVLTreeNode<T> Node;
public:bool Insert(T key){Node* newnode = new Node(key);if (_root == nullptr){_root = newnode;return true;}Node* cur = _root;Node* parent = nullptr;//尋找插入位置while (cur){if (key > cur->_key){parent = cur;cur = cur->_right;}else if (key < cur->_key){parent = cur;cur = cur->_left;}else return false;}//插入新的節點newnode->_parent = parent;if (key < parent->_key) parent->_left = newnode;else parent->_right = newnode;//更新平衡因子//插入后AVL樹平衡，無需調整//插入后AVL樹高度增加，繼續向上調整cur = newnode;while (parent){if (cur == parent->_left) parent->_bf--;else parent->_bf++;//檢查平衡因子狀態if (parent->_bf == 0) break;else if (parent->_bf == 1 || parent->_bf == -1){cur = parent;parent = parent->_parent;}//不平衡，旋轉else if (parent->_bf == 2 || parent->_bf == -2){if (parent->_bf == 2){//左單旋if (parent->_right->_bf == 1){_RotateL(parent);}else{_RotateRL(parent);}}else{//右單旋if (parent->_left->_bf == -1){_RotateR(parent);}else{_RotateLR(parent);}}break;}else{cout << "error: _bf";break;}}return true;}Node* Find(const T& key){Node* cur = _root;while (cur){if (key > cur->_key) cur = cur->_right;else if (key < cur->_key) cur = cur->_left;else return cur;}return nullptr;}size_t Size(){return _Size(_root);}void InOrder(){_InOrder(_root);}int GETHeight(){return _GETHeight(_root);}bool IsBalance(){return _isBalance(_root);}	
private:bool _isBalance(Node* root){if (root->_bf >= 2 || root->_bf <= -1) return false;int HeightLeft = _GETHeight(root->_left);int HeightRight = _GETHeight(root->_right);if (abs(HeightRight - HeightLeft) > 1) return false;return _isBalance(root->_left) && _isBalance(root->_right);}int _GETHeight(Node* root){if (root == nullptr) return 0;return max(_GETHeight(root->_left), _GETHeight(root->_right)) + 1;}void _InOrder(Node* root){if (root == nullptr) return;_InOrder(root->_left);cout << root->_key << " ";_InOrder(root->_right);}size_t _Size(Node* root){if (root == nullptr) return 0;size_t SizeLeft = _Size(root->_left);size_t SizeRight = _Size(root->_right);return SizeLeft + SizeRight + 1;}//右旋void _RotateR(Node* pParent){Node* LSub = pParent->_left;Node* LSubR = LSub->_right;Node* pPParent = pParent->_parent;if(LSubR)LSubR->_parent = pParent;pParent->_left = LSubR;LSub->_right = pParent;pParent->_parent = LSub;LSub->_parent = pPParent;if (pParent == _root) _root = LSub;else{if (pPParent->_left == pParent) pPParent->_left = LSub;else pPParent->_right = LSub;}//更新平衡因子LSub->_bf = pParent->_bf = 0;}//左旋void _RotateL(Node* pParent){Node* RSub = pParent->_right;Node* RSubL = RSub->_left;Node* pPParent = pParent->_parent;if (RSubL) RSubL->_parent = pParent;pParent->_right = RSubL;RSub->_left = pParent;pParent->_parent = RSub;RSub->_parent = pPParent;if (pParent == _root) _root = RSub;else{if (pPParent->_left == pParent) pPParent->_left = RSub;else pPParent->_right = RSub;}//更新平衡因子RSub->_bf = pParent->_bf = 0;}void _RotateRL(Node* pParent){Node* RSub = pParent->_right;Node* RSubL = RSub->_left;int bf = RSubL->_bf;_RotateR(RSub);_RotateL(pParent);RSub->_bf = 0;if (bf == 1){RSub->_bf = 0;pParent->_bf = -1;}else if (bf == -1){pParent->_bf = 0;RSub->_bf = 1;}else{RSub->_bf = pParent->_bf = 0;}}void _RotateLR(Node* pParent){Node* LSub = pParent->_left;Node* LSubR = LSub->_right;int bf = LSubR->_bf;_RotateL(LSub);_RotateR(pParent);LSub->_bf = 0;if (bf == 0){LSubR->_bf = LSubR->_bf = 0;}else if (bf == 1){LSub->_bf = -1;pParent->_bf = 0;}else if (bf == -1){LSub->_bf = 0;pParent->_bf = 1;}}private:Node* _root = nullptr;
};void test_AVL01()
{int a[] = { 8, 3, 1, 10, 6, 4, 7, 14, 13 };//int a[] = { 4, 2, 6, 1, 3, 5, 15, 7, 16, 14 };AVLTree<int> t1;for (auto e : a){int i = 1;t1.Insert(e);//cout << "Insert:" << e << "->" << t1.IsBalance() << endl;}cout << t1.GETHeight() << endl;t1.InOrder();//cout << t1.IsBalance() << endl;
}void test_AVL02()
{const int N = 10000000;vector<int> v;v.reserve(N);srand(time(0));for (size_t i = 0; i < N; i++){v.push_back(rand() + i);//cout << v.back() << endl;}size_t begin2 = clock();AVLTree<int> t;for (auto e : v){t.Insert(e);//cout << "Insert:" << e << "->" << t.IsBalance() << endl;}size_t end2 = clock();cout << "Insert:" << end2 - begin2 << endl;//cout << t.IsBalance() << endl;cout << "Height:" << t.GETHeight() << endl;cout << "Size:" << t.Size() << endl;size_t begin1 = clock();// 確定在的值for (auto e : v){t.Find(e);}// 隨機值/*for (size_t i = 0; i < N; i++){t.Find((rand() + i));}*/size_t end1 = clock();cout << "Find:" << end1 - begin1 << endl;
}