前面的算法文章，更新了許多 專題系列 。包括：滑動窗口、動態規劃、加強堆、二叉樹遞歸套路 等。

還沒讀過的小伙伴可以關注一下，在主頁中點擊對應鏈接查看哦~

接下來的一段時間，將持續 「力扣高頻題」 系列文章，想刷 力扣高頻題 的小伙伴也可以關注一波哦 ~

言歸正傳，今天我們來講一道中等難度的力扣高頻題，與 接雨水問題 很類似哦~

11. 盛最多水的容器

給定一個長度為 n 的整數數組 height 。有 n 條垂線，第 i 條線的兩個端點是 (i, 0) 和 (i, height[i]) 。找出其中的兩條線，使得它們與 x 軸共同構成的容器可以容納最多的水。返回容器可以儲存的 最大水量 。

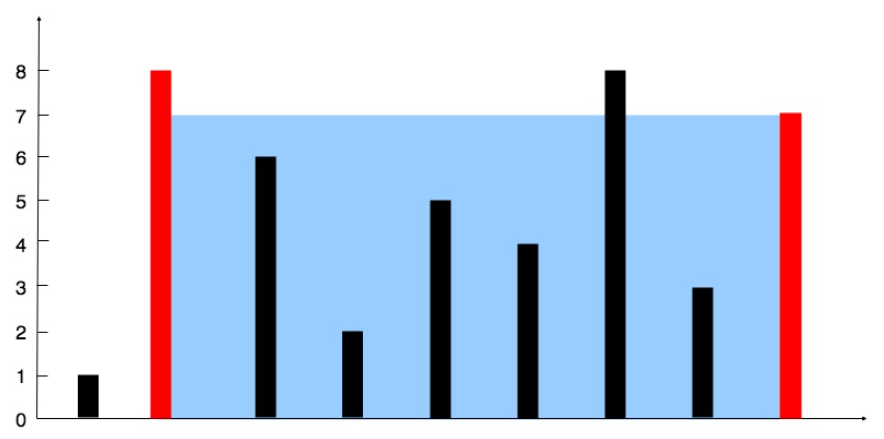
示例 1：

輸入： [1,8,6,2,5,4,8,3,7]

輸出： 49

解釋： 圖中垂直線代表輸入數組 [1,8,6,2,5,4,8,3,7] 。在此情況下，容器能夠容納水（表示為藍色部分）的最大值為 49 。

示例 2：

輸入： [1,1]

輸出： 1

• 提示：
• n == height.length
• 2 <= n <= $10^5$
• 0 <= height[i] <= $10^4$

思路分析

一個很簡單的道理：能夠裝多少水量，取決于較短的豎線的 長度 ，以及兩根豎線之間的 距離 。

總水量 = 較短的長度（高度） × 距離（寬度）

由于兩個因素變量是相乘的關系，兩者的改變可能會導致結果呈現此起彼伏的變化，不便于討論分析。因此，需要想辦法控制變量。

顯然，若 高度一樣 的情況下，距離越長 能夠存儲的 最大水量越大 。最終要找的就是最大值，因此設置兩個指針一開始先分別指向數組的首尾（此時距離最長），然后逐步縮小該距離（即移動雙指針）。

要想當 距離縮短 時，反而獲得更大的存儲水量，唯一的辦法就是 增高較短邊的長度 。

思考到這里，做題的思路就逐步清晰了：縮短距離時，優先要移動此時較短的指針，只有這樣才能有增大最終答案的 可能性 。

如果錯誤的先移動了較長的邊，高度只有可能 不變或減小 ，距離 一定會減小，導致了最終答案也一定是 變小，做了無用功。

代碼

public static int maxArea(int[] h) {int max = 0;int l = 0;int r = h.length - 1;while (l < r) {max = Math.max(max, Math.min(h[l], h[r]) * (r - l));if (h[l] > h[r]) {r--;} else {l++;}}return max;
}

代碼解釋

1. 當前最大水量的計算：左右指針中最短的邊 × 距離l - r。
2. 通過if - else語句判斷雙指針此時指向的高度，誰短移動誰 。
3. 設置max變量更新最大值，遍歷結束（兩指針相遇），得到最終最大蓄水量。

• 復雜度分析
  • 時間復雜度：$O(N)$，雙指針一共遍歷數組一遍即可。
  • 空間復雜度：$O(1)$ 。

---

刷過類似題目的小伙伴很容易想到一道很經典的題目 接雨水 問題，點贊關注，下次我們接著講！

---

~ 點贊 ~ 關注 ~ 星標 ~ 不迷路 ~！！！

回復「ACM紫書」獲取 ACM 算法書籍 ~
回復「算法導論」獲取 算法導論第3版 ~

在看 + 轉發

讓你的小伙伴們一起來學算法吧！！