240627_關于CNN中圖像維度變化問題
在學習一些經典模型時,其中得維度變化關系總搞不太明白,集中學習了以下,在此作以梳理總結:
一般來說涉及到的維度變換都是四個維度,當batch size=4,圖像尺寸為640*640,RGB三通道時,此時維度就是4×3×640×640。3的意思是RGB三通道,如果你傳入的圖像是單通道圖像,此時維度就是4×1×640×640。
當然有些圖你看著是一個黑白圖,但是他還是有可能是一張RGB三通道圖,具體怎么區分呢。右擊圖片打開屬性,打開詳細信息,里面可以看到位深度,位深度為24,則為RGB圖,位深度為8,則為單通道圖。此處就是一個坑,圖像分割任務中,標簽往往是單通道圖,但是有時從網上找到的數據集看起來是黑白的,但是實際訓練就會報錯,查看了才發現位深度是24,需要用python代碼進行修改,具體跳轉240627_圖像24位深度(RGB圖)轉為8位深度(單通道圖)-CSDN博客。
當維度是三維時,就是沒有batch size這個維度,可以理解為這個維度指的是其中一張圖。
標準卷積
以U_Net為例
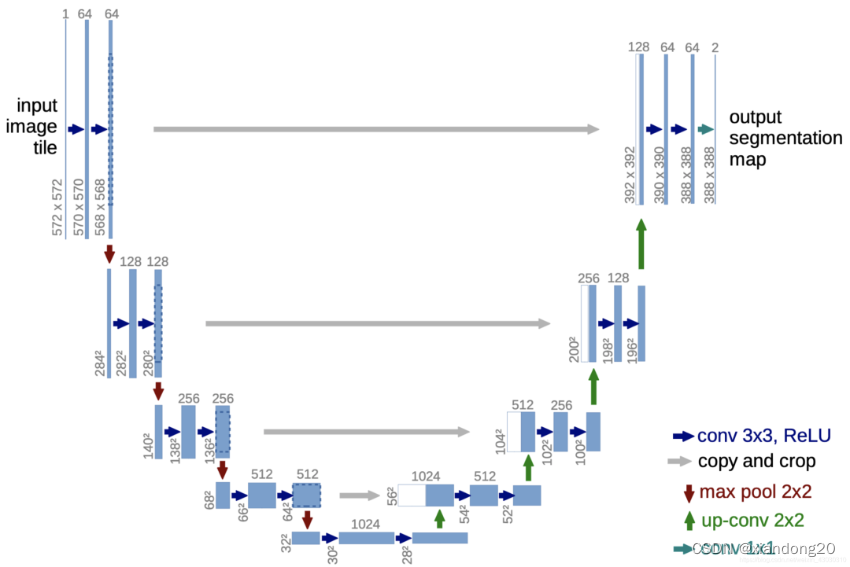
# U_Net網絡的簡單結構,就寫了一層,其他同理
block1=block_down(3,64)
x1_use=block1(x) # torch.Size([3, 64, 568, 568])
x1=self.maxpool(x1_use) # torch.Size([3, 64, 284, 284])'''
block down中卷積核的定義為
self.conv1 = nn.Conv2d(inp_channel, out_channel, kernel_size=3, stride=1,padding_mode='reflect')
self.conv2 = nn.Conv2d(out_channel, out_channel, kernel_size=3, stride=1,padding_mode='reflect')
'''
卷積輸出的計算公式為
h e i g h t o u t = ( h e i g h t i n ? h e i g h t k e r n e l + 2 ? p a d d i n g ) s t r i d e + 1 height_{out}=\frac{(height_{in}-height_{kernel}+2*padding)}{stride}+1 heightout?=stride(heightin??heightkernel?+2?padding)?+1
w i d t h o u t = ( w i d t h i n ? w i d t h k e r n e l + 2 ? p a d d i n g ) s t r i d e + 1 width_{out}=\frac{(width_{in}-width_{kernel}+2*padding)}{stride}+1 widthout?=stride(widthin??widthkernel?+2?padding)?+1
輸入3張572572的RGB圖像(3×3×572×572),經過3×3卷積(padding=0,stride=1),此時的計算公式為
h e i g h t o u t = w i d t h o u t = ( 572 ? 3 + 2 ? 0 ) 1 + 1 = 570 height_{out}=width_{out}=\frac{(572-3+2*0)}{1}+1=570 heightout?=widthout?=1(572?3+2?0)?+1=570
一共經過兩層之后尺寸為568568,因為kernel的out_channel定義的是64,所以一共有64個卷積核,輸出通道為64,此時維度為3×64×568×568。
然后經過最大池化層,尺寸除以2,通道數不變,此時維度為3×64×284×284
其余層數同理
| batch_size | height | width | in_channel | out_channel | |
|---|---|---|---|---|---|
| Input | 3 | 572 | 572 | 3 | |
| Kernel | 3 | 3 | 3 | 64 | |
| Output | 3 | 570 | 570 | 64 |
1×1卷積
以ResNet50為例
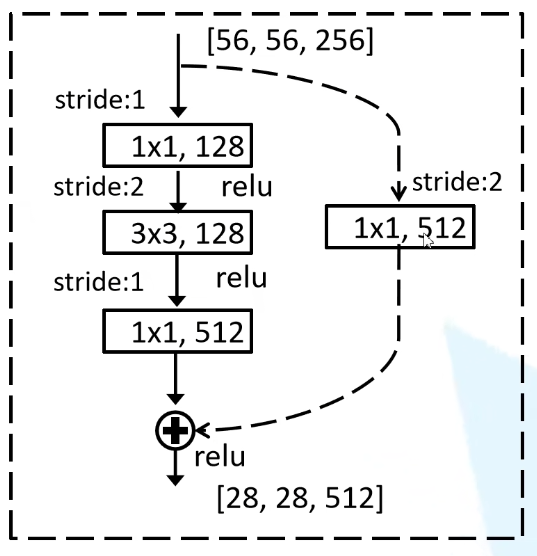
我們看shortcuts分支(右半弧線分支),這個分支輸入一張維度為1×256×56×56的圖像,經過一個1×1卷積(stride=2,padding=0),此時經過上述公式計算,尺寸為28,輸出通道數為512。
| batch_size | height | width | in_channel | out_channel | |
|---|---|---|---|---|---|
| Input | 1 | 56 | 56 | 256 | |
| Kernel | 1 | 1 | 256 | 512 | |
| Output | 1 | 28 | 28 | 512 |
當然也有特殊情況,1×1卷積,卷積核尺寸為1,步長為1,padding=0,通過以上公式可以計算出來尺寸不會發生變化,但通道數可以發生改變,由卷積核數量決定。
全連接層
全連接層就是把所有的像素點都攤開,攤成尺寸為1×1,通道數好多好多,其卷積核尺寸和輸入尺寸一致,輸出 通道數就是卷積核個數
| batch_size | height | width | in_channel | out_channel | |
|---|---|---|---|---|---|
| Input | 1 | 56 | 56 | 256 | |
| Kernel | 56 | 56 | 256 | 512 | |
| Output | 1 | 1 | 1 | 512 |
總結
輸出通道數就是卷積核個數
卷積后尺寸計算公式就是
h e i g h t o u t = ( h e i g h t i n ? h e i g h t k e r n e l + 2 ? p a d d i n g ) s t r i d e + 1 height_{out}=\frac{(height_{in}-height_{kernel}+2*padding)}{stride}+1 heightout?=stride(heightin??heightkernel?+2?padding)?+1
w i d t h o u t = ( w i d t h i n ? w i d t h k e r n e l + 2 ? p a d d i n g ) s t r i d e + 1 width_{out}=\frac{(width_{in}-width_{kernel}+2*padding)}{stride}+1 widthout?=stride(widthin??widthkernel?+2?padding)?+1


)



)
)





)
)




