數據結構 —— 哈夫曼樹
- 哈夫曼樹
- 定義
- 構造算法
- 特性
- 應用
- 哈夫曼編碼
- 核心概念
- 工作原理
- 特點
我們今天來看哈夫曼樹:
哈夫曼樹
哈夫曼樹(Huffman Tree),是一種特殊的二叉樹,由D.A. Huffman在1952年提出,主要用于數據壓縮,特別是哈夫曼編碼(Huffman Coding)中。以下是關于哈夫曼樹的全面概念:
定義
哈夫曼樹是一種帶權路徑長度最短的二叉樹,也稱為最優二叉樹。它是在給定一組具有不同權重的葉子節點(通常代表數據中的符號或字符)的情況下,通過特定的構建算法得到的。該樹的特點是,所有葉子節點位于最底層或倒數第二層,且沒有度為1的節點(除了根節點可能外),同時保證了從根節點到任何葉子節點的路徑上的權值之和(即帶權路徑長度)最小。
舉個例子:
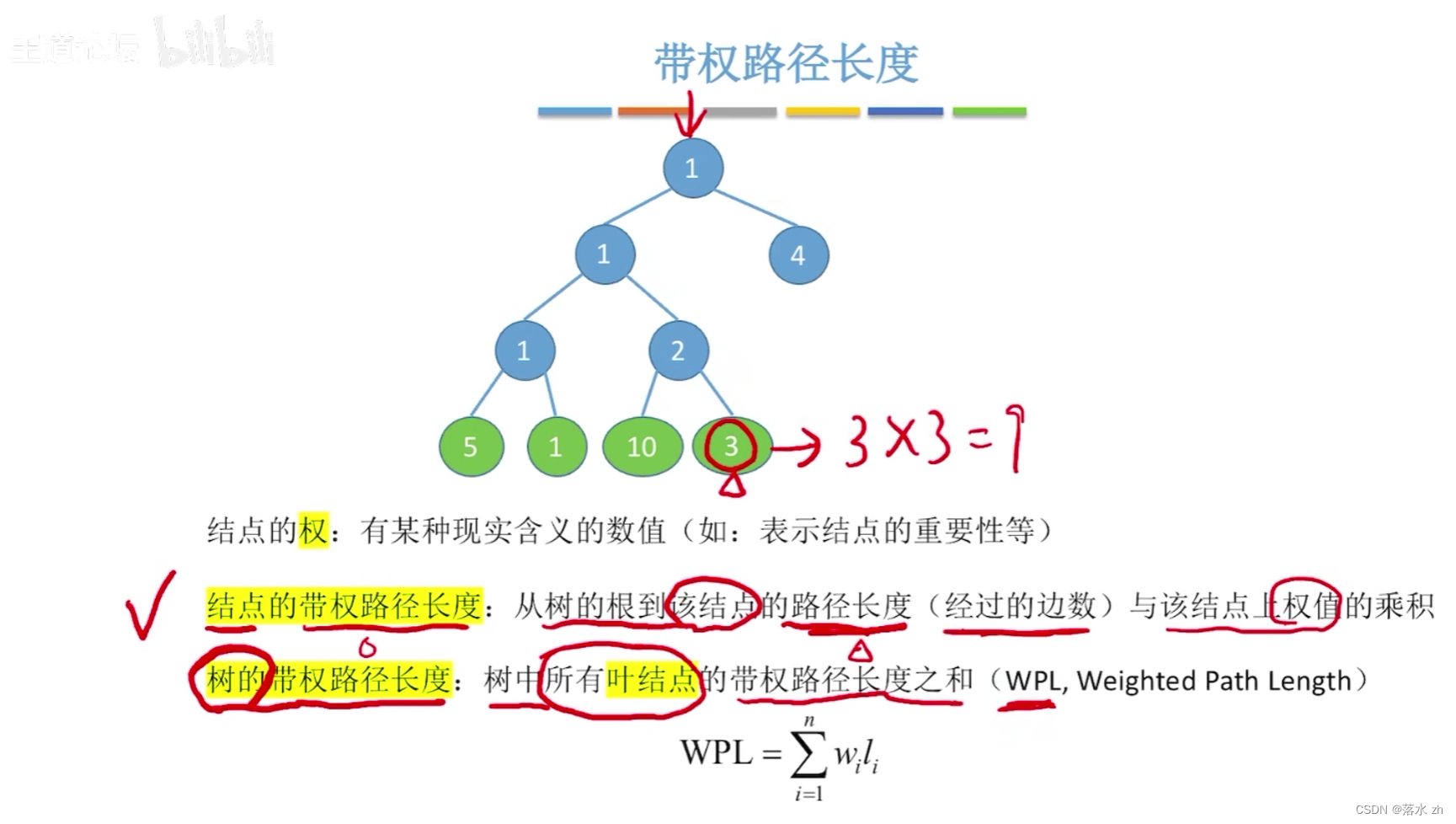
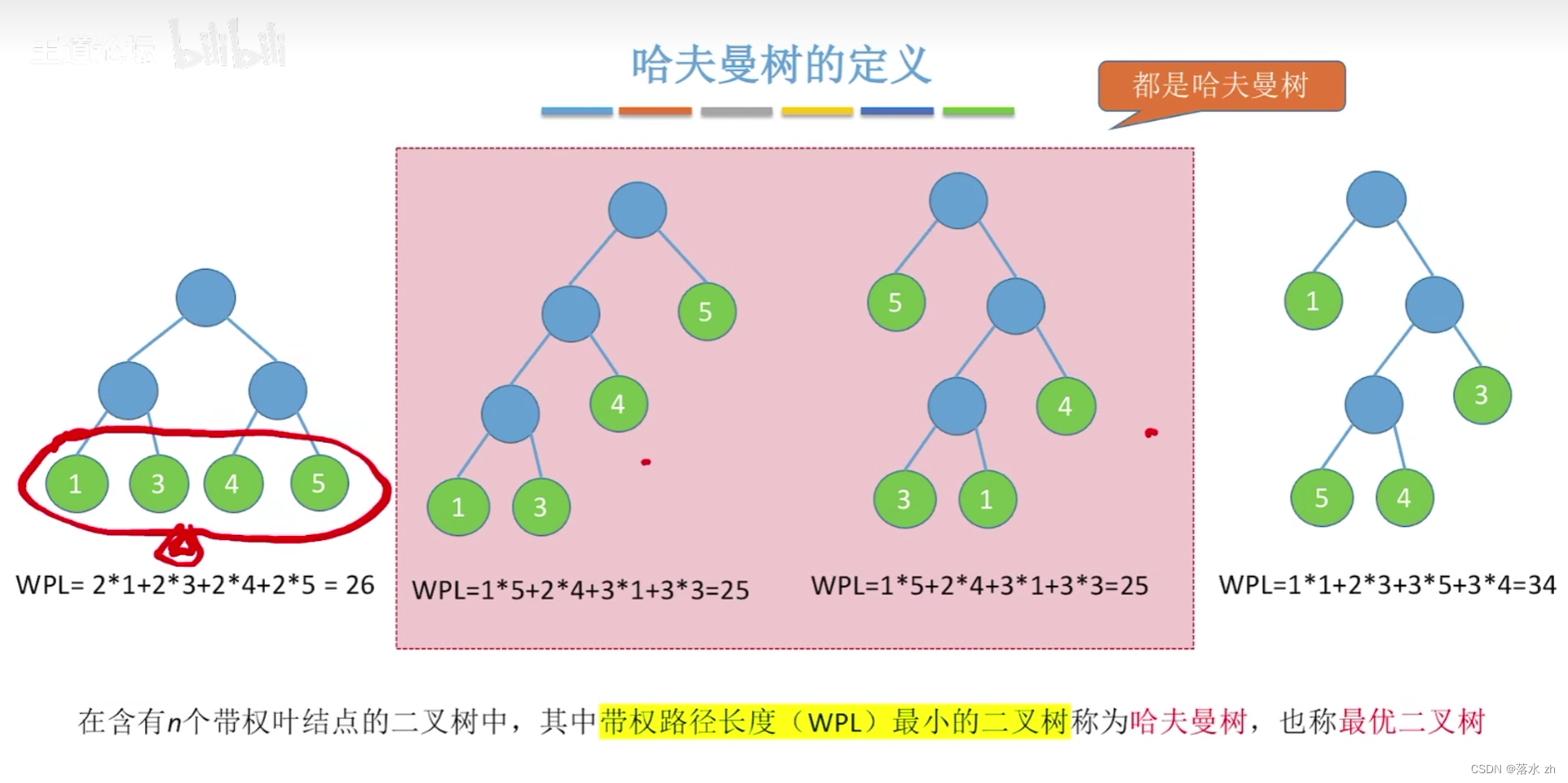
構造算法
- 初始化:將每個權重作為一個葉子節點,放入一個優先隊列(優先級基于節點權重,通常使用最小堆實現)。
- 合并節點:從隊列中取出兩個權重最小的節點,創建一個新的內部節點,其權重為這兩個節點的權重之和,新節點作為這兩個節點的父節點。
- 重復步驟2:將新創建的節點放回優先隊列,重復上述過程,直到隊列中只剩下一個節點,該節點即為哈夫曼樹的根節點。
- 生成編碼:從根到每個葉子節點的路徑可以轉化為一個唯一的二進制字符串(路徑上向左走記為0,向右走記為1),這個字符串就是該葉子節點代表的字符的哈夫曼編碼。
 這里我沒有寫得那么復雜,我用一個vector維護森林,并且排好序,然后依次拿出構造哈夫曼樹:
這里我沒有寫得那么復雜,我用一個vector維護森林,并且排好序,然后依次拿出構造哈夫曼樹:
#pragma once
#include<algorithm>
#include<iostream>
#include<vector>// 定義霍夫曼樹節點結構體
template<class T>
struct HuffManTreeNode
{
public:// 構造函數,初始化節點數據、左孩子和右孩子HuffManTreeNode(T data):_data(data), _leftchild(nullptr), _rightchild(nullptr){}// 拷貝構造函數,用于復制已有節點的信息HuffManTreeNode(HuffManTreeNode<T>* node):_data(node->_data), _leftchild(node->_leftchild), _rightchild(node->_rightchild){}// 析構函數~HuffManTreeNode(){}// 創建新節點并返回指針HuffManTreeNode<T>* CreateNode(T data){HuffManTreeNode<T>* newnode = new HuffManTreeNode(data);return newnode;}// 根據已有節點創建新節點并返回指針HuffManTreeNode<T>* CreateNode(HuffManTreeNode<T>* node){HuffManTreeNode<T>* newnode = new HuffManTreeNode(node);return newnode;}// 向樹中插入新節點void Insert(HuffManTreeNode<T>*& node, T data){HuffManTreeNode<T>* newnode = CreateNode(data);if (newnode == nullptr){perror("new fail");return;}if (node->_leftchild == nullptr){node->_leftchild = newnode;}else if (node->_rightchild == nullptr){node->_rightchild = newnode;}return;}// 向樹中插入已有節點void Insert(HuffManTreeNode<T>*& node, HuffManTreeNode<T>* temp){if (node->_leftchild == nullptr){node->_leftchild = CreateNode(temp);}else if (node->_rightchild == nullptr){node->_rightchild = CreateNode(temp);}return;}// 重載賦值運算符HuffManTreeNode<T>& operator=(const HuffManTreeNode<T>* node){if (this == node){return *this;}_data = node->_data;_leftchild = node->_leftchild;_rightchild = node->_rightchild;return *this;}// 數據成員T _data;// 左右孩子指針HuffManTreeNode<T>* _leftchild;HuffManTreeNode<T>* _rightchild;
};// 中序遍歷霍夫曼樹
template<class T>
void Inorder(HuffManTreeNode<T>* node)
{if (node == nullptr){return;}Inorder(node->_leftchild); // 遍歷左子樹std::cout<< node->_data << " "; // 訪問當前節點Inorder(node->_rightchild); // 遍歷右子樹
}
#include"Huffman.h"int main()
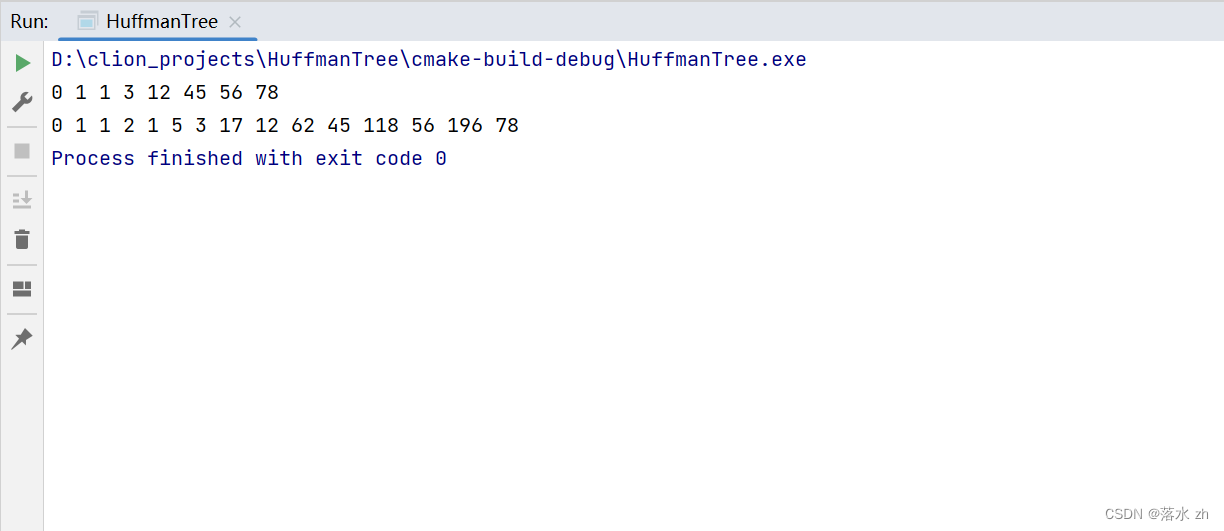
{std::vector<int> vt = {1,45,12,56,78,0,1,3};std::sort(vt.begin(),vt.end());for(auto e : vt){std::cout << e << " ";}std::cout<<std::endl;//創建哈夫曼樹HuffManTreeNode<int>* node = new HuffManTreeNode(vt[0]+vt[1]);node->Insert(node,vt[0]);node->Insert(node,vt[1]);for(int i = 2 ; i < vt.size(); i++){HuffManTreeNode<int>* temp = node;node = node->CreateNode(node->_data +vt[i]);node->Insert(node,temp);node->Insert(node,vt[i]);}Inorder(node);return 0;
}
特性
- 最優性:在所有葉子節點數量相同且節點權值已知的二叉樹中,哈夫曼樹的帶權路徑長度是最小的。
- 編碼效率:哈夫曼編碼根據字符出現的頻率分配編碼,高頻字符的編碼較短,低頻字符的編碼較長,從而在整體上達到高效的數據壓縮效果。
- 無損編碼:哈夫曼編碼是一種無損數據壓縮方法,可以完全恢復原始數據。
- 自適應性:雖然經典哈夫曼編碼基于靜態概率模型,但存在變體如自適應哈夫曼編碼,能夠根據數據流動態調整編碼表,適用于數據統計特性隨時間變化的情況。
應用
- 數據壓縮:廣泛應用于文本、圖像、音頻等數據的無損壓縮。
- 通信系統:優化數據傳輸,減少帶寬需求。
- 文件存儲:減小文件大小,節約存儲空間。
- 編譯器:用于詞法分析中的關鍵字識別,通過為常用關鍵字分配較短編碼,提高解析速度。
哈夫曼編碼
哈夫曼編碼(Huffman Coding)是一種高效的熵編碼(Entropy Encoding)方法,用于無損數據壓縮。它是基于哈夫曼樹(Huffman Tree)構造的一種數據編碼方式,由David A. Huffman在1952年提出。以下是哈夫曼編碼的核心概念、工作原理以及特點:
核心概念
哈夫曼編碼的基本思想是根據數據中各個符號(如字符、像素值等)出現的頻率來為它們分配不同的編碼,出現頻率高的符號分配較短的編碼,而頻率低的符號則分配較長的編碼。這樣,當整個數據集被編碼時,由于高頻符號使用的短編碼能頻繁重復,從而實現整體數據量的壓縮。
工作原理
- 頻率統計:首先統計待編碼數據中每個符號出現的頻率。
- 構建哈夫曼樹:使用頻率作為權重,通過哈夫曼樹的構造算法(見前述哈夫曼樹的構造過程),構建一棵二叉樹。在這個過程中,每次都將兩個最小頻率的節點合并成一個新的節點,新節點的頻率是兩個子節點頻率之和。
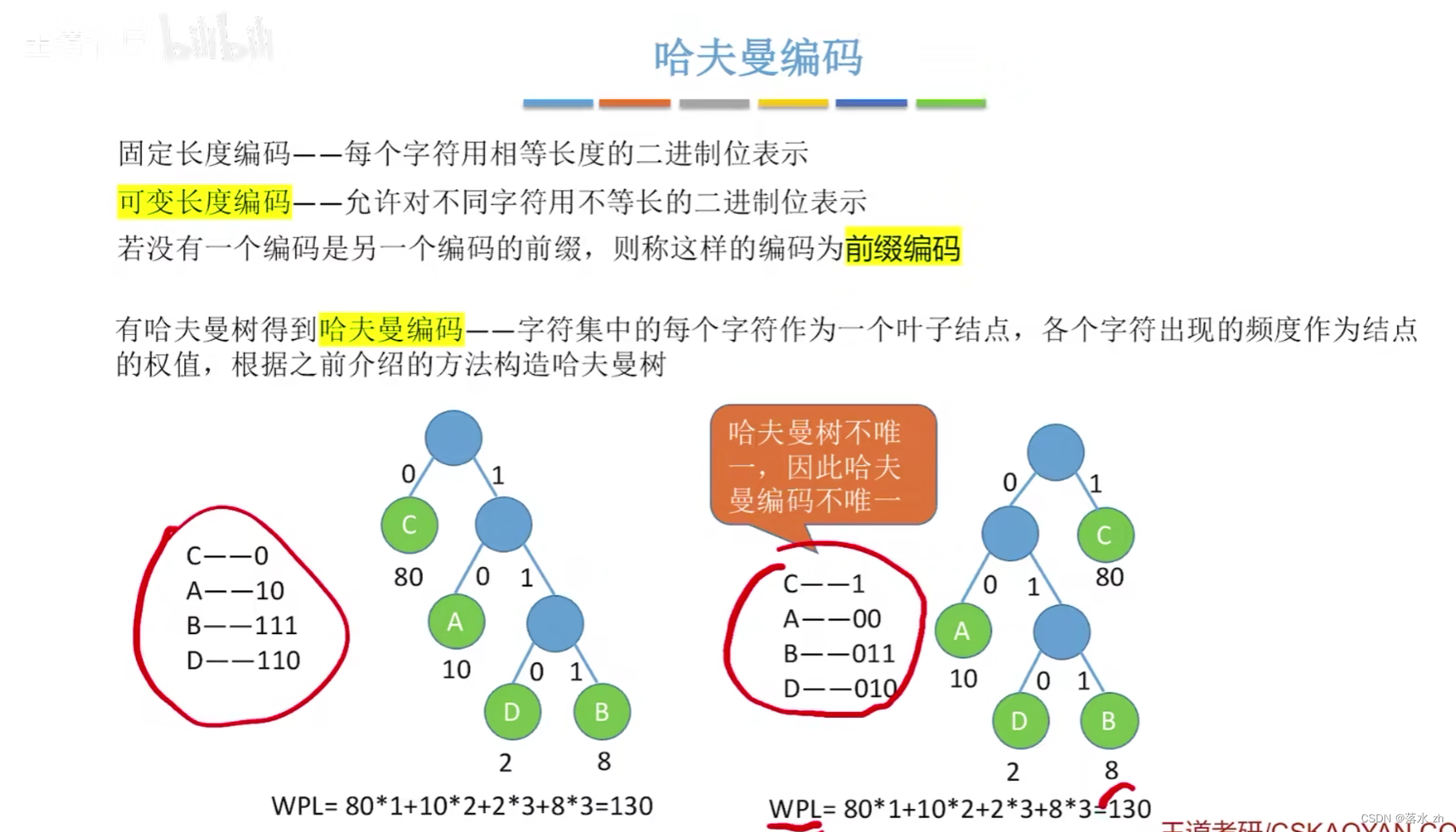
- 生成編碼:從哈夫曼樹的根到每個葉子節點的路徑定義了該葉子節點代表符號的編碼。具體來說,向左分支時編碼添加一個“0”,向右分支時添加一個“1”。因此,葉子節點越深,其對應的編碼就越長。
- 編碼數據:使用生成的哈夫曼編碼表對原始數據進行編碼,即將數據中的每個符號替換為其對應的編碼字符串。
特點
- 無損編碼:哈夫曼編碼是一種無損數據壓縮技術,意味著解碼后可以完全恢復原始數據。
- 自適應性:雖然標準哈夫曼編碼需要預先知道數據的概率分布,但可以通過動態哈夫曼編碼技術,在不知道全部數據的情況下逐步更新編碼表,適應數據流的變化。
- 效率:在所有前綴編碼(即任意編碼都不會是另一個編碼的前綴)中,哈夫曼編碼提供了理論上的最優平均編碼長度,即熵的上限。
- 簡單性:盡管編碼效率高,哈夫曼編碼的算法實現相對直接且易于理解。
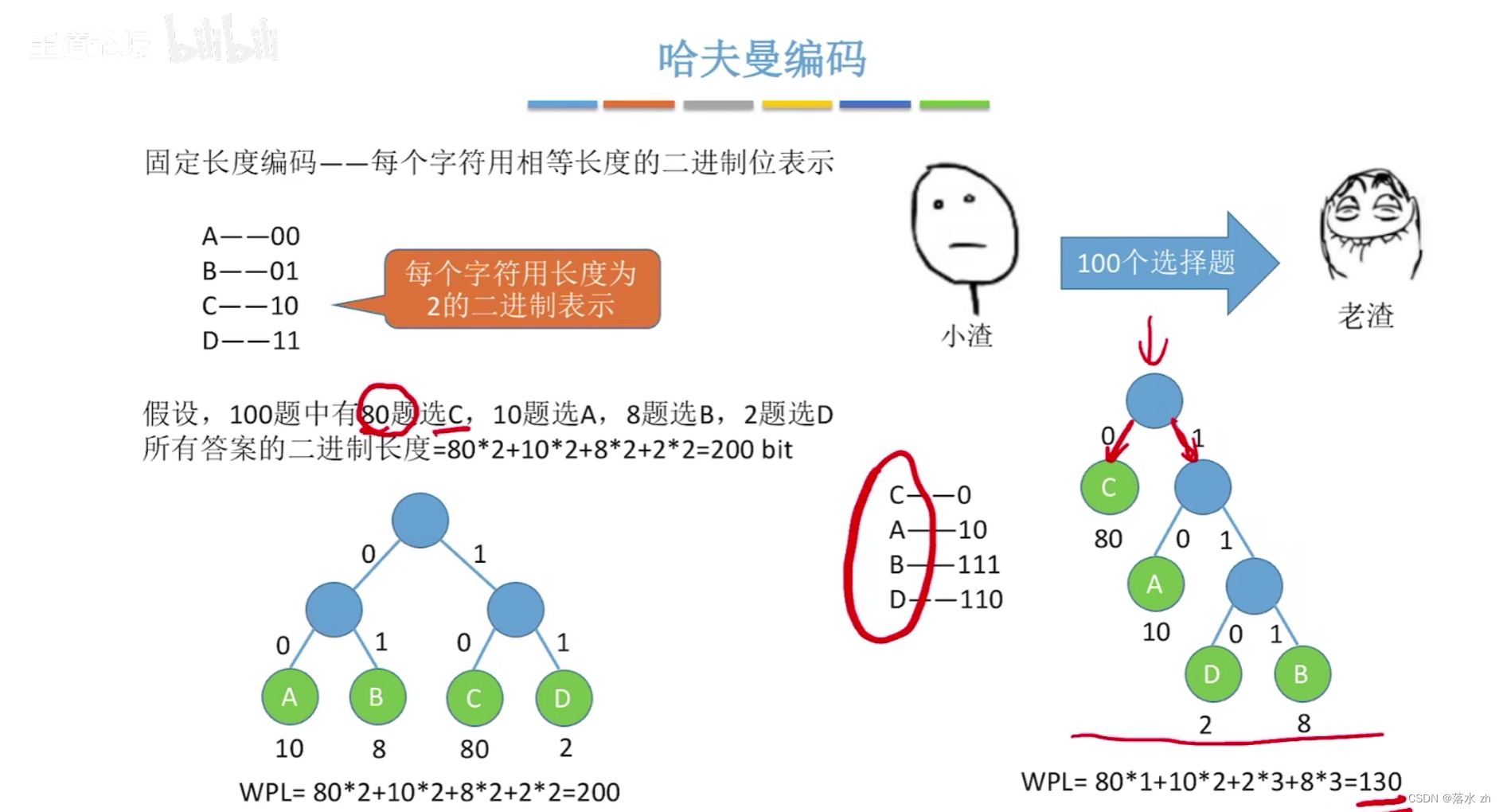

![[面試題]計算機網絡](http://pic.xiahunao.cn/[面試題]計算機網絡)


















