機器學習就是讓機器具備找一個函數的能力
帶有未知的參數的函數稱為模型
通常一個模型的修改,往往來自于對這個問題的理解,即領域知識。
損失函數
- 平均絕對誤差(Mean Absolute Error,MAE)

- 均方誤差(Mean Squared Error,MSE)
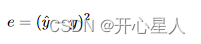
- 交叉熵(cross entropy):有一些任務中 y 和 ^y 都是概率分布,這個時候可能會選擇交叉熵
梯度下降
解一個最優化的問題。把未知的參數找一個數值出來,看代哪一個數值進去可以讓損失 L 的值最小。
梯度下降(gradient descent)是經常會使用優化的方法
假設只有一個未知參數w,怎么樣找一個 w 讓損失的值最小。
首先要隨機選取一個初始的點 w0,計算在 w 等于 w0 的時候,參數 w 對損失L的微分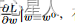
計算在這一個點,在 w0 這個位置的誤差表面的切線斜率,也就是這一條藍色的虛線,它的斜率,如果這一條虛線的斜率是負的,代表說左邊比較高,右邊比較低。在這個位置附近,左邊比較高,右邊比較低。如果左邊比較高右邊比較低的話,就把 w 的值變大,就可以讓損失變小。如果算出來的斜率是正的,就代表左邊比較低右邊比較高。左邊比較低右邊比較高,如果左邊比較低右邊比較高的話,就代表把 w 變小了,w 往左邊移,可以讓損失的值變小
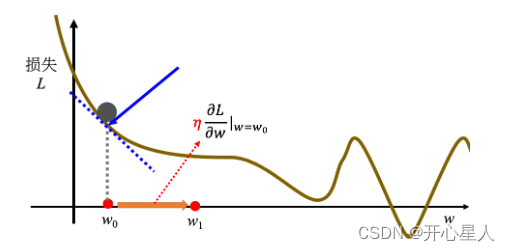
w左右移動的步伐大小取決于:
- 1、斜率,斜率大步伐就跨大一點,斜率小步伐就跨小一點
- 2、學習率(learning rate)η 也會影響步伐大小。學習率是自己設定的,如果 η 設大一點,每次參數更新就會量大,學習可能就比較快。如果 η 設小一點,參數更新就很慢,每次只會改變一點點參數的數值。(在做機器學習,需要自己設定,不是機器自己找出來的,稱為超參數(hyperparameter))
所以w的更新如下:
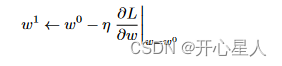
不斷地移動 w 的位置,最后會停下來。往往有兩種情況會停下來
- 1、設定更新次數的超參數:上限可能會設為 100 萬次,參數更新 100 萬次后,就不再更新了
- 2、當不斷調整參數,調整到一個地方,它的微分的值就是這一項,算出來正好是 0 的時候,如果這一項正好算出來是 0,0 乘上學習率 η 還是 0,所以參數就不會再移動位置
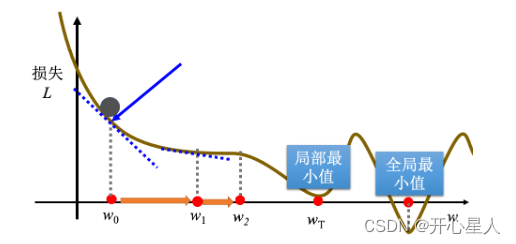
局部最小值和全局最小值問題
梯度下降有一個很大的問題,沒有找到真正最好的解,沒有找到可以讓損失最小的 w。
如果在梯度下降中,w0 是隨機初始的位置,也很有可能走到 wT 這里,訓練就停住了,無法再移動 w 的位置。(事實上局部最小值是一個假問題,在做梯度下降的時候,真正面對的難題不是局部最小值。)
對于有多個未知參數,w、b。
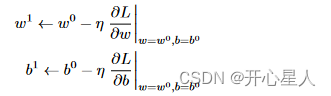
激活函數
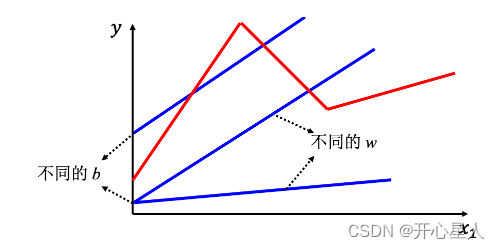
線性模型,不管如何設置 w 跟 b,永遠制造不出紅色線,永遠無法用線性模型制造紅色線。顯然線性模型有很大的限制,這一種來自于模型的限制稱為模型的偏差,無法模擬真實的情況。
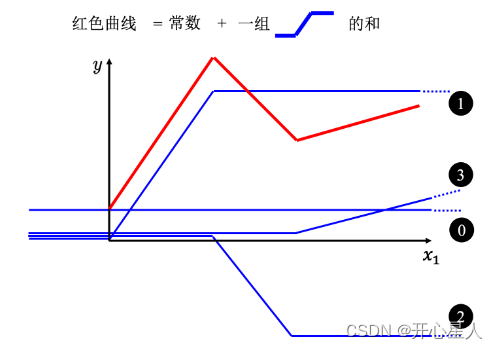
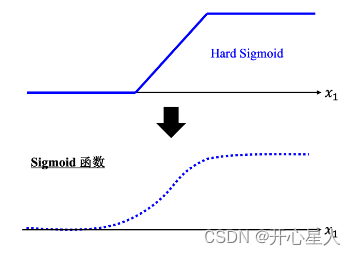
所以需要寫一個更復雜的、更有靈活性的、有未知參數的函數。紅色的曲線可以看作是一個常數再加上一群 Hard Sigmoid 函數。Hard Sigmoid 函數的特性是當輸入的值,當 x 軸的值小于某一個閾值(某個定值)的時候,大于另外一個定值閾值的時候,中間有一個斜坡。所以它是先水平的,再斜坡,再水平的。所以紅色的線可以看作是一個常數項加一大堆的藍色函數(Hard Sigmoid)
假設 x 跟 y 的關系非常復雜也沒關系,就想辦法寫一個帶有未知數的函數。直接寫 Hard Sigmoid 不是很容易,但是可以用一條曲線來理解它,用Sigmoid 函數來逼近 Hard Sigmoid,
Sigmoid 函數的表達式為
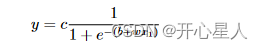
Hard Sigmoid 可以看作是兩個修正線性單元(Rectified Linear Unit,ReLU)的加總
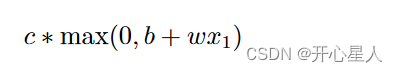
Sigmoid 和 ReLU 是最常見的激活函數
https://blog.csdn.net/caip12999203000/article/details/127067360
批量
實際使用梯度下降的時候,會把 N 筆數據隨機分成一個一個的批量(batch),一組一組的。每個批量里面有 B 筆數據,所以本來有 N筆數據,現在 B 筆數據一組,一組叫做批量
本來是把所有的數據拿出來算一個損失,現在只拿一個批量里面的數據出來算一個損失
所以實現上每次會先選一個批量,用該批量來算 L1,根據 L1 來算梯度,再用梯度來更新參數,接下來再選下一個批量算出 L2,根據 L2 算出梯度,再更新參數,再取下一個批量算出 L3,根據 L3 算出梯度,再用 L3 算出來的梯度來更新參數。
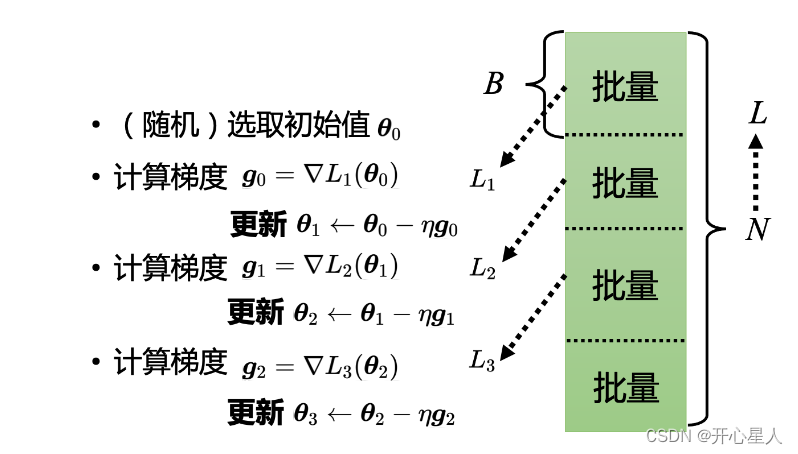
所以并不是拿 L 來算梯度,實際上是拿一個批量算出來的 L1, L2, L3 來計算梯度。把所有的批量都看過一次,稱為一個回合(epoch),每一次更新參數叫做一次更新。
舉個例子,假設有 10000 筆數據,即 N 等于 10000,批量的大小是設 10,也就 B 等于 10。10000 個樣本(example)形成了 1000 個批量,所以在一個回合里面更新了參數 1000 次,所以一個回合并不是更新參數一次,在這個例子里面一個回合,已經更新了參數 1000 次了。
所以做了一個回合的訓練其實不知道它更新了幾次參數,有可能 1000 次,也有可能 10 次,取決于它的批量大小有多大。 批量大小是超參數
深度學習
Sigmoid 或 ReLU 稱為神經元(neuron),很多的神經元稱為神經網絡(neural network)
每一排稱為一層,稱為隱藏層(hidden layer),很多的隱藏層就“深”,這套技術稱為深度學習。
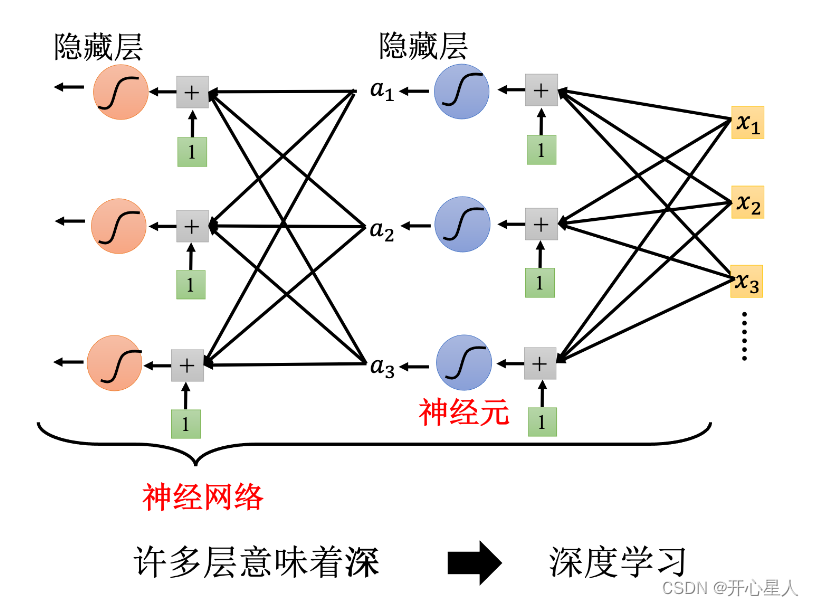
深度學習的訓練會用到反向傳播(BackPropagation,BP),其實它就是比較有效率、算梯度的方法。







和 Python 庫 SymPy 進行符號數學計算的教程)











