1、求解最優化問題的算法 通常需要經過一系列的步驟，在每個步驟都面臨多種選擇。對于許多最優化問題，使用動態規劃算法求最優解有些殺雞用牛刀了，可以使用更簡單、更高效的算法
貪心算法（greedy algorithm）就是這樣的算法，它在每一步都做出當時看起來最優的選擇。也就是說，它總是做出局部最優的選擇，寄希望通過這些選擇導致全局最優解

2、貪心算法 并不保證得到最優解，但對很多問題 確實可以求得最優解

1、活動選擇問題

一個調度競爭共享資源的 多個活動的問題，目標是 選出一個最大的互相兼容的活動集合。假定有一個 n 個活動的集合 S = {a1, a2, …, an}，這些活動使用同一資源（例如一個階梯教室），每個活動 a_i 都有一個開始時間 s_i 和 一個結束時間 f_i，其中 0 ≤ s_i < f_i < ∞。如果被選中， a_i 發生在 [si, fi) 期間。如果 a_i 和 a_j 滿足 [s_i, f_i) 和 [s_j, f_j) 不重疊，則稱它們是兼容的
當 s_i ≥ f_j 或 s_j ≥ f_i 時，a_i 和 a_j 是兼容的。希望選出一個最大兼容活動的子集

假定活動 已按結束時間的單調遞增順序排列：

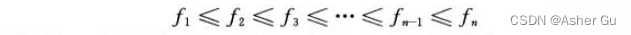
可以通過動態規劃方法 將這個問題分為兩個子問題，然后 將兩個子問題的最優解 結合成原問題的一個最優解。在確定該將 哪些子問題用于最優解時，要考慮幾種選擇
貪心算法只需考慮一種選擇（即貪心的選擇），在做貪心選擇時，子問題之一必定是空的，因此，只留下一個非空子問題。找到一種遞歸貪心算法 來解決活動調動問題，并將遞歸算法轉化為迭代算法，以完成貪心方法的過程

1.1 最優子結構

A_ij = A_ij U { a_k } U A_kj，而且 S_ij 中最大兼容任務子集 A_ij 包含 I A_ij I = | A_ik | + | A_kj l + 1 個活動
用剪切一粘貼辦法證明最優解
A_ij 必然包含兩個子問題 S_ik 和 S_kj 的最優解

用 c[i, j] 表示集合 S_ij 的最優解的大小

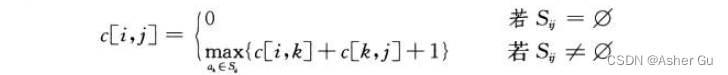
1.2 貪心選擇

假如 發現所有子問題都可以選擇出一個活動加入到最優解，對于活動選擇問題， 只需要考慮一個選擇，貪心選擇

應該選擇這樣一個活動，選出它后 剩下的資源應能被盡量多的其他任務所用。現在考慮可選的活動， 其中必然有一個最先結束。應該選擇S中最早結束的活動，因為 它剩下的資源可供它之后盡量多的活動使用

選擇最早結束的活動并不是本問題唯一的貪心選擇方法：也可以選擇 最晚開始活動（開始要把 活動開始時間 從晚到早排序（貪心 之前的排序很重要），然后把滿足條件的順次加入進去 就行）

定理16.1 考慮任意非空子問題s，且 a_j 是 A_k 中結束時間最早的活動，則 a_m 在 S_k 的某個最大兼容子集中

雖然 可以用動態規劃方法 求解活動選擇問題，但并不需要這樣做（此外，并未檢查活動選擇問題 是否具有重疊子問題性質）。相反，可以反復選擇 最早結束的活動，保留與此活動兼容的活動，重復這一過程，直至無剩余活動可選
而且，因為 總是選擇最早結束的活動，所以選擇的活動 在結束時間上總是嚴格遞增的，只需要 按結束時間的單調遞增順序 去處理所有活動，每個活動只考慮一次

貪心算法 通常都是這種自頂向下的設計：做出一個選擇，然后求解剩下的那個子問題

1.3 遞歸貪心算法

輸入為兩個數組 s 和 f，表示活動的開始 和 結束時間，下標 k 指出要求解的子問題 S_k, 以及 問題規模 n

為了方便 算法初始化，添加一個虛擬活動 a_0，其結束時間 f_0 = 0（因為上來的活動就是 k + 1），求解原問題 即可調用RECURSIVE-ACTIVITY-SELECTOR(s, f, 0, n)

RECURSIVE-ACTIVITY-SELECTOR(s, f, k, n)
1  m = k + 1
2  while m <= n and s[m] < f[k]
3     m = m + 1
4  if m <= n
5     return {a_m} ∪ RECURSIVE-ACTIVITY-SELECTOR(s, f, m, n) // 下一代從 k = m 開始
6  else return ?

可能因為 m>n 而終止，這意味著我們已經檢查了 S_k 中所有活動，未找到與 a_k 兼容者

假定活動 已經按結束時間排好序，則遞歸調用 RECURSIVE-ACTIVITY-SELECTOR(s, f, 0, n) 的運行時間為 Θ(n)，在整個遞歸調用過程中，每個活動只被 while 循環檢查一次

1.4 迭代貪心算法

1、將算法轉換為 迭代形式。過程 RECURSIVE-ACTIVITY-SELECTOR 幾乎就是“尾遞歸”。它以一個對自身的遞歸調用 再接一次并集操作結尾。將一個尾遞歸過程 改為 迭代形式 通常是很直接的，實際上，某些特定語言的編譯器可以自動完成這一工作

GREEDY-ACTIVITY-SELECTOR(s, f)
1.  n = s.length
2.  A = {a_1}
3.  k = 1
4.  for m = 2 to n
5.      if s[m] >= f[k]
6.          A = A ∪ {a_m}
7.          k = m
8.  return A

與遞歸版本類似，在輸入活動已按結束時間排序的前提下，GREEDY-ACTIVITY-SELECTOR 的運行時間為 Θ(n)

2、并不是所有貪心方法都能得到最大兼容活動子集。在剩余兼容活動中 選擇 持續時間最短者 不能得到最大集。在剩余兼容活動選擇與其他剩余活動重疊最少者 也是同理

3、假定有一組活動，需要將它們安排到一些教室，任意活動都可以在任意教室進行。希望使用最少的教室完成所有活動。設計一個高效的貪心算法來安排哪些活動在哪個教室進行

(這個問題稱為 區間圖著色問題(interval-graph coloring problem))。可以構建一個區間圖，其中表示活動的節點，邊連接不兼容的活動。要求用最少的顏色對圖的頂點進行著色，使用所有鄰項頂點之間的不同顏色

這個算法的關鍵在于貪心策略：
總是優先使用已經空閑的講堂來安排新的活動
只有當沒有空閑講堂時，才添加新的講堂

不能用貪心了，O(n³) 是 i 從0到 n，j 從 i + 1 到 n，k 從 i 到 j
因為 c[i, k] + c[k, j] + V_k
希望最大化兼容活動的總價值，可以使用動態規劃（Dynamic Programming, DP）來實現

def find_latest_non_conflicting(activities, n):for j in range(n-1, -1, -1):if activities[j][1] <= activities[n][0]:return jreturn -1def activity_selection_with_values(activities):# 按結束時間排序activities.sort(key=lambda x: x[1])# 動態規劃數組n = len(activities)dp = [0] * (n + 1)for i in range(1, n + 1):# 當前活動的值value = activities[i-1][2]# 查找最新的與當前活動兼容的活動j = find_latest_non_conflicting(activities, i-1)# 遞推公式if j != -1:dp[i] = max(dp[i-1], value + dp[j+1])else:dp[i] = max(dp[i-1], value)return dp[n]# 示例活動 (開始時間, 結束時間, 價值)
activities = [(1, 3, 5), (2, 5, 6), (4, 6, 5), (6, 7, 4), (5, 8, 11), (7, 9, 2)]
print("最大價值：", activity_selection_with_values(activities))

2、貪心算法原理

1、通過 做出一系列選擇來求出問題的最優解。在每個決策點，它做出在當時看來最佳的選擇。這種 啟發式策略 并不保證總能找到全局最優解

2、設計貪心算法步驟

1. 將最優化問題 轉換為這樣的形式：對其做出一次選擇后，只剩下一個子問題需要求解
2. 證明做出貪心選擇后，原問題總是 存在最優解，即貪心選擇是安全的
3. 證明做出貪心選擇后，剩余的子問題 滿足性質：其最優解與貪心選擇組合 即可得到原問題的最優解，這樣就得到了最優子結構

2.1 貪心選擇性質

1、可以通過做出局部最優（貪心）選擇 來構建全局最優解

2、與動態規劃 先求解子問題才能 進行第一次選擇不同，貪心算法 在進行第一次選擇之前 不求解任何子問題，一個動態規劃算法是 自底向上 進行計算的，而一個貪心算法 通常是自頂向下的，進行一次又一次選擇，將給定問題實例 變得更小

3、必須證明每個步驟 做出貪心選擇 能生成全局最優解。這種證明 通常首先考查 某個子問題的最優解，然后用貪心選擇 替換某個其他選擇 來修改此解，從而得到一個相似但更小的子問題

進行貪心選擇時 不得不考慮 眾多選擇，通常意味著 可以改進貪心選擇，使其更為高效
例如，在活動選擇問題中，假定 已經將活動按結束時間單調遞增順序 排好序，則對每個活動能夠只處理一次。通過對輸入進行預處理 或者 使用適合的數據結構（通常是優先隊列），通常可以使得貪心選擇更快速，從而得到更有效的算法

2.2 最優子結構

1、如果一個問題的最優解 包含其子問題的最優解，則稱此問題具有 最優子結構性質。此性質是 能否應用動態規劃 和 貪心算法的關鍵要素

活動選擇問題為例，如果一個子問題 S_ij 的最優解包含活動a_k，那么必然也包含子問題 S_ik 和 S_kj 的最優解
如果知道 S_ij 的最優解應該包含 哪個活動 a_k，就可以組合 a_k 以及 S_ik 和 S_kj 的最優解中所有活動來構造 S_ij 的最優解

2、論證最優子結構：將子問題的最優解 與 貪心選擇 組合在一起就能生成原問題的最優解。這種方法隱含對于子問題 使用了數學歸納法，證明了 每個步驟進行貪心選擇都會生成原問題的最優解

2.3 貪心對動態規劃

1、0-1背包問題：一個正在搶劫商店的小偷 發現了 n 個商品，第 i 個商品價值 v_i 美元，重 w_i 磅，v_i 和 w_i 都是整數。小偷希望 拿走價值盡貨高的商品，但他的背包 最多能容納 W 磅重的商品， W是一個整數。應該拿哪些商品
（稱這個問題是 0-1 背包問題， 因為對每個商品，小偷要么把它完整拿走， 要么把它留下，不能只拿走一部分）

2、在分數背包問題 中，設定與 0-1 背包問題是一樣的，不同的是：小偷可以拿走其一部分，而不是 只能做出二元 (0-1) 選擇

3、兩個背包問題都具有 最優子結構性質。對0-1背包問題，考慮重量不超過 W 而 價值最高的裝包方案。如果 將商品 j 從此方案中刪除，則剩余商品 必須是重量不超過 W - w_j 的價值最高的方案

貪心策略 可以求解分數背包問題，而不能求解 0-1 背包問題
為了求解分數背包問題，首先計算每個商品的每磅價值 v_i / w_i 。遵循貪心策略，首先盡量多地拿 每磅價值最高的商品。通過將背包按每磅價值排序，貪心算法的運行時間可為 O(nlgn)

證明分數背包問題具有貪心選擇性質

拿走商品 1 的策略對 0-1 背包問題無效 是因為小偷無法裝滿背包，空閑空間降低了方案的有效每磅價值。在 0-1 背包問題中，當考慮是否 將一個商品裝入背包時，必須比較包含 此商品的子問題的解 與 不包含它的子問題的解，然后才能做出選擇。這會導致大量的重疊子問題——動態規劃的標識

設計動態規劃算法求解 0-1 背包問題，要求運行時間為 O(nW)，n 為商品數量，W 是小偷能放進背包中的最大商品總重量
動規不用事先排序
K含義：K[考慮過的物品， 剩余空間重量]

0-1-KNAPSACK(n, W)Initialize an (n + 1) by (W + 1) table Kfor i = 1 to nK[i, 0] = 0for j = 1 to WK[0, j] = 0for i = 1 to nfor j = 1 to Wif j < i.weightK[i, j] = K[i - 1, j]elseK[i, j] = max(K[i - 1, j], K[i - 1, j - i.weight] + i.value)

3、赫夫曼編碼

1、根據每個字符的出現頻率，赫夫曼算法 構造出字符的最優二進制表示

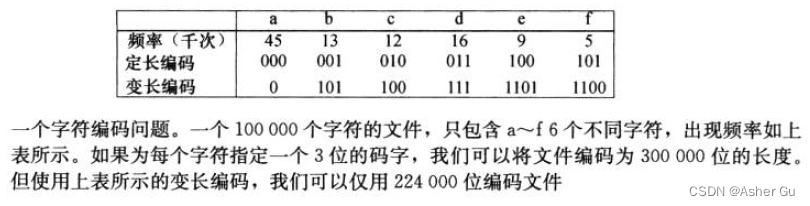
每個字符用一個唯一的一二進制串表示，稱為碼字。如果使用定長編碼，需要用3位表示6個字符：a=000, b=001, …, f=101。這種方法需要300,000個二進制位來編碼文件

2、變長編碼 可以達到 比定長編碼好得多的壓縮率，其思想是賦予高頻字符 短碼字，賦予低頻字符 長碼字。上圖顯示了六個字符的一種變長編碼：1位的a表示，4位的f表示。因此，這種編碼表示此文件
(45?1+13?3+12?3+16?3+9?4+5?4)?1000=224,000位
與定長編碼相比 節約了25%的空間，這是 此文件的最優字符編碼

3.1 前綴碼

1、只考慮所謂前綴碼，即沒有任何字符是其他字符的前綴。與任何字符編碼相比，前綴碼 都可以保證達到最優數據壓縮率。因此 只關注前綴碼，不會喪失一般性

前綴碼的作用是 簡化解碼過程。由于沒有碼字是其他碼字的前綴，編碼文件的開始碼字是無歧義的。可以簡單地識別出 開始碼字，將其轉換回 原字符，然后對編碼文件剩余部分 重復這種解碼過程

在上節的例子中，二進制串 001011101 可以唯一地解析為 0·0·101·1101，解碼為 aabec

2、解碼過程 需要前綴碼的一種方便的表示形式，以便 可以容易地截取開始字符。一種二叉樹表示 可以滿足這種需求，其葉結點為 給定的字符。字符的二進制碼字 用從根結點到該字符葉結點的簡單路徑表示，其中 0 意味著 “轉向左孩子”，1 意味著 “轉向右孩子”
注意，編碼樹并不是二叉搜索樹，因為葉節點并未有序排列，而內部結構并不包含 字符關鍵字

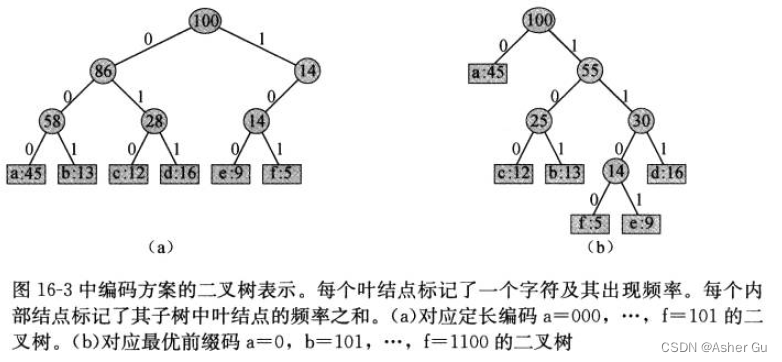
文件的最優編碼方案總是對應一棵 滿(full) 二叉樹，即每個非葉節點都有兩個孩子結點。前文給出的定長編碼實例 不是最優的，因為它的二叉樹表示 并非 滿二叉樹
若 C 為字母表 且 所有字符的出現頻率 均為正數，則最優編碼樹對應的樹結構恰有 |C| 個葉結點，每個葉結點對應字母表中一個字符，且恰有 |C|?1 個內部結點

對字母表C中的每個字符c，令屬性 c.freq 表示 c 在文件中出現的頻率，令 d_T(c) 表示c的葉結點在樹中的深度。注意，d_T(c) 也是字母c的碼字的長度。則編碼該文件需要

3.2 構造赫夫曼編碼

1、貪心算法來構造最優前綴碼，它的正確性證明 依賴于 貪心選擇性質 和 最優子結構

2、算法自底向上地構建出 對應最優編碼的二叉樹 T
它從 |C| 個葉結點開始，執行 |C|?1 次“合并”操作 創建出最終的二叉樹。算法使用一個以 屬性 freq 為關鍵字的最小優先隊列 Q，以識別 兩個最低頻率的對象 將其合并。當合并兩個對象時，得到的新對象的頻率 等于原來兩個對象頻率之和
（根 搜索樹不一樣，沒有其他對節點的順序限制之后，只需要 讓頻率大的靠近根，頻率小的遠離根）

HUFFMAN(C)
1  n = |C|
2  Q = C
3  for i = 1 to n-1
4     allocate a new node z
5     z.left = x = EXTRACT-MIN(Q) // 把代價最小的刪除并返回
6     z.right = y = EXTRACT-MIN(Q)
7     z.freq = x.freq + y.freq
8     INSERT(Q, z)
9  return EXTRACT-MIN(Q) // return the root of the tree

由于字母表 包含6個字符，初始隊列大小為 n=6

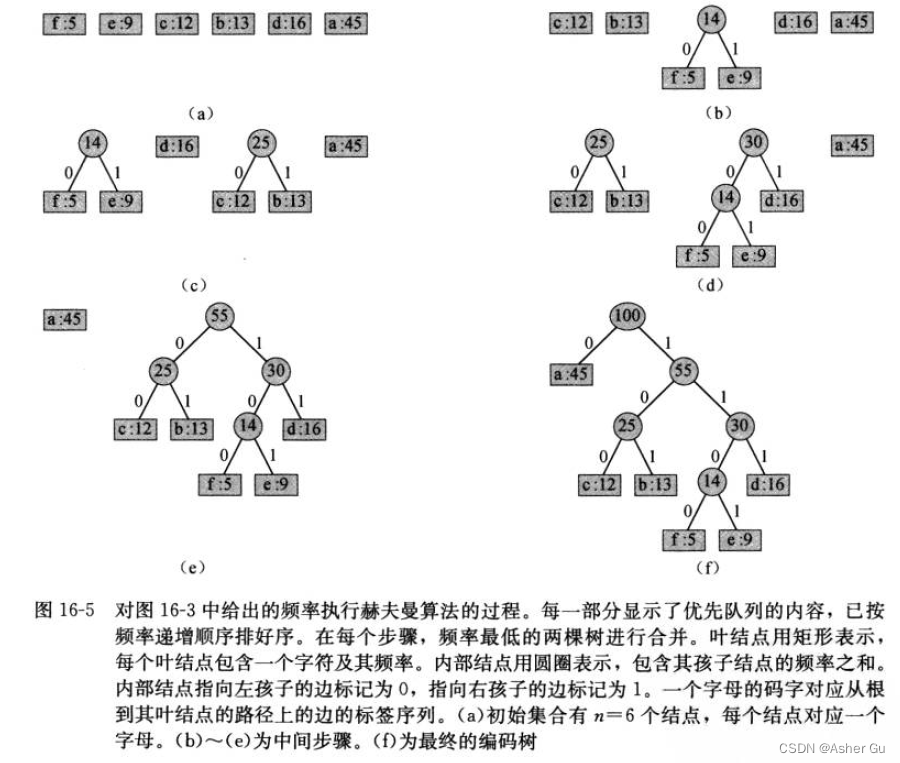
for循環 反復從隊列中提取兩個頻率最低的結點 x 和 y，將它們合并為 一個新結點z，替代它們。z的頻率為 x 和 y 的頻率之和
結點z將 x 作為其左孩子，將 y 作為其右孩子（順序是不重要的，交換左右孩子會生成一種不同的編碼，但代價完全一樣）。經過 n?1 次合并后，第9行返回隊列中剩下的唯一結點——編碼樹的根結點

3、為了分析赫夫曼算法的運行時間，假定 Q 是使用最小二叉堆實現的（參見第6章）。在第2行用 BUILD-MIN-HEAP過程（參見6.3節）將 Q 初始化，花費時間為 O(n)。第3～8行的 for 循環執行 n?1 次，且每個堆操作需要 O(lgn) 的時間，所以循環對總時間的貢獻為 O(nlgn)。因此，處理一個n個字符的集合，HUFFMAN 的總運行時間為 O(nlgn)

3.3 赫夫曼算法的正確性

1、確定最優前綴碼的問題 具有貪心選擇 和 最優子結構性質

2、（1）令 C 為一個字符表，其中每個字符 c∈C 都有一個頻率 c.freq。令 x 和 y 是 C 中頻率最低的兩個字符。那么存在 C 的一個最優前綴碼，x 和 y 的碼字長度相同，且 只有最后一個二進制位不同（即是 兄弟結點，在最優的基礎上 每次合并仍是最優，即可合并）

證明 證明的思想是令 T 表示任意一棵最優前綴碼所對應的編碼樹，對其進行修改，得到表示另外一個最優前綴碼的編碼樹，使得在新樹中，x 和 y 是深度最大的葉結點，且它們為兄弟結點
如果 可以構造這樣一棵樹，那么 x 和 y 的碼字將有相同長度，且只有最后一位不同

令 a 和 b 是 T 中深度最大的兄弟葉結點， 不失一般性， 假定a.freq <= b.freq 且 x.freq＜= y.freq。由于 x.freq 和 y.freq 是葉結點中最低的兩個頻率，而 a.freq 和 b.freq 是兩個任意頻率。因此， 我們有 x.freq <= a.freq 且 y.freq <= b.freq
交換 x 和 a 生成一棵新樹 T’, 井在 T 中交換 b 和 y 生成一棵新樹 T"
T和T’的代價差為

類似地，交換 x 和 b 也不能增加代價，所以 B(T′) ? B(T’‘) 也是非負的。因此 B(T′′) < B(T)，由于 T 是最優的，我們有 B(T′’) = B(T)，這意味著 B(T′′) = B(T)。因此，T’’ 也是最優樹，且 x 和 y 是其中深度最深的兄弟結點，引理成立

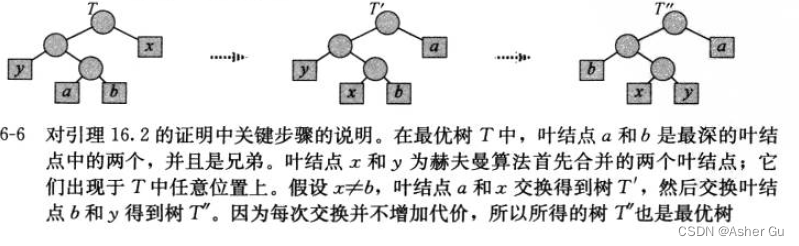
3、通過合并來構造最優樹的過程，可以 從合并出現頻率最低的兩個字符 這樣一個貪心選擇開始。為什么這是一個貪心選擇？可以將每一次合并操作的代價 看做 被合并的兩項的頻率之和

在每個步驟 可選擇的所有合并操作中，HUFFMAN 選擇是 代價最小的那個，下面的引理證明了構造最優前綴碼的問題具有最優子結構性質

（2）令 C 為一個含有 n 個字符表，其中每個字符 c∈C 都有一個頻率 c.freq。令 C’ 為 C 去棹字符 x 和 y, 加入一個新字符 z 后得到的宇母表，即 C’ = C - {x, y} ∪{z}，z.freq = x.freq + y.freq。令 T’ 為字母表 C’ 的任意一個最優前綴碼對應的編碼樹。于是 可以將 T’ 中葉結點 z 替換為一個以 x 和 y 為孩子的內部結點，得到樹 T, 而 T 表示字母表C的 一個最優前綴碼

證明：用樹 T’ 的代價 B(T’) 來表示樹 T 的代價 B(T)

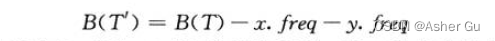
用反證法來證明引理。假定 T 對應的前綴碼并不是 C 的最優前綴碼，存在最優編碼樹 T’’ 滿足 B(T′‘) < B(T)。不失一般性(由引理 16.2)，T’’ 包含兄弟結點 x 和 y，令 T’’ 將 T 中 x,y 及它們的父結點替換為葉結點 z 得到的樹，其中 z.freq = x.freq + y.freq（T’‘’ 對應 T’，T’’ 對應 T）

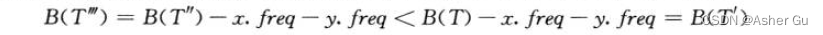
與 T’ 對應 C’ 的一個最優前綴碼的假設矛盾。因此 T 必然表示字符表 C 的一個最優前綴碼，即最優 T 一定包含 最優 T’'（最優子結構）

4、由（1）（2），過程 HUFFMAN 會生成一個最優前綴碼

5、