前言

上文說到了樹，有人認為二叉樹是樹的每一個分支都有兩個子節點。其實這也對。但二叉樹在此基礎上還做了限制。比如區別了左子樹與右子樹。也就是說，當二叉樹的根只有一個孩子時，也需要知道這個是左孩子還是右孩子。就是因為這個原因，讓二叉樹的性能相對于樹有了明顯的提高。也讓二叉樹成了一個全新的概念，而不是樹的一個特別情況而已。

概念

二叉樹（Binary Tree） 是樹的一種常見形式，它是一棵有序樹。它的子節點最多只有兩個，分為左子樹和右子樹，哪怕只有一個子節點，也要區分出是左子樹還是右子樹，如果顛倒了，就是一棵新的二叉樹了。二叉樹的度最大為2。
二叉樹常被用于實現二叉查找樹和二叉堆，樹的很多問題都可以通過$BFS廣度優先搜索算法$或$DFS深度優先搜索算法（DepthFirstSearch）$解決。

特別的二叉樹

滿二叉樹

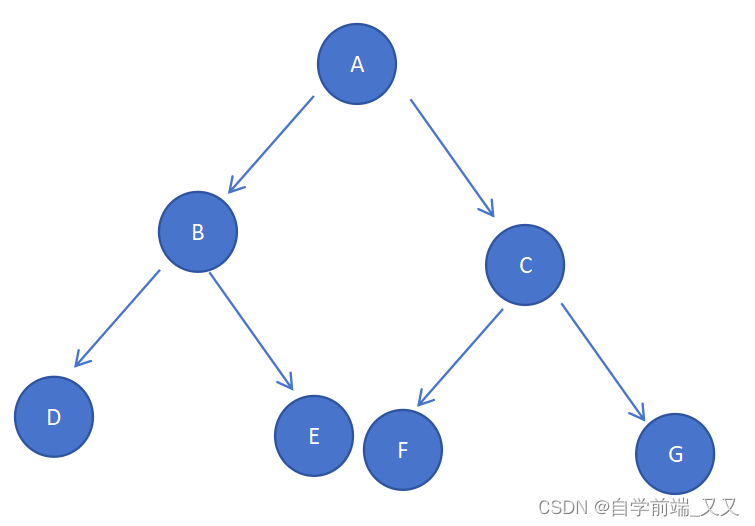
一個二叉樹，如果它有子節點，并且子節點數都是最大值($在每一層上沒有空缺的位置$)，則稱為滿二叉樹。一個滿二叉樹，除了根節點，其余節點數都是2個一起出現的，如 B與C、D與E、F與G。 所以如果滿二叉樹的層級為K，則
節點數 ： $2^k?1$ 。這個 -1，就是因為根節點只有一個。
如果節點數為N，則
高度 : h = $lo{g}_2(N+1)$

完全二叉樹

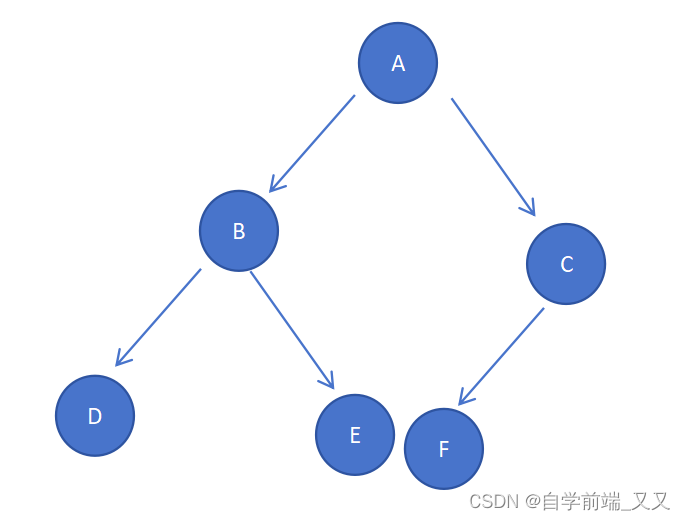
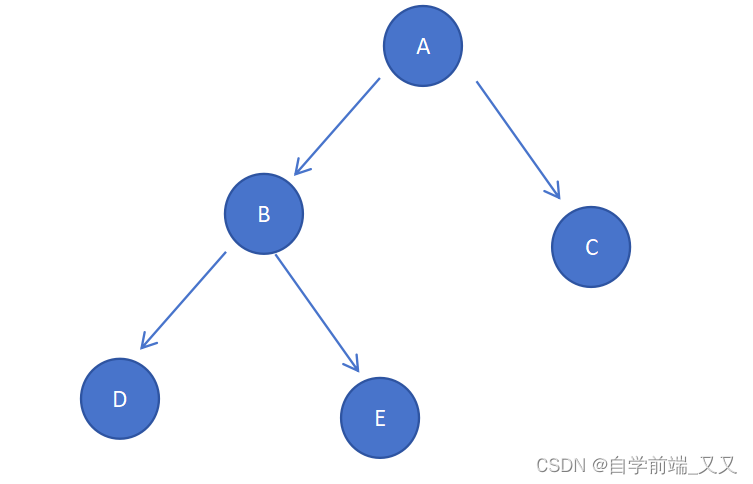
滿二叉樹是完全二叉樹特殊情況，當滿二叉樹從最后的節點依次減少時，形成的就是完全二叉樹。完全二叉樹從根節點、左子樹、右子樹的順序執行，一直到樹結束都沒有空缺的節點。

存儲結構

順序存儲

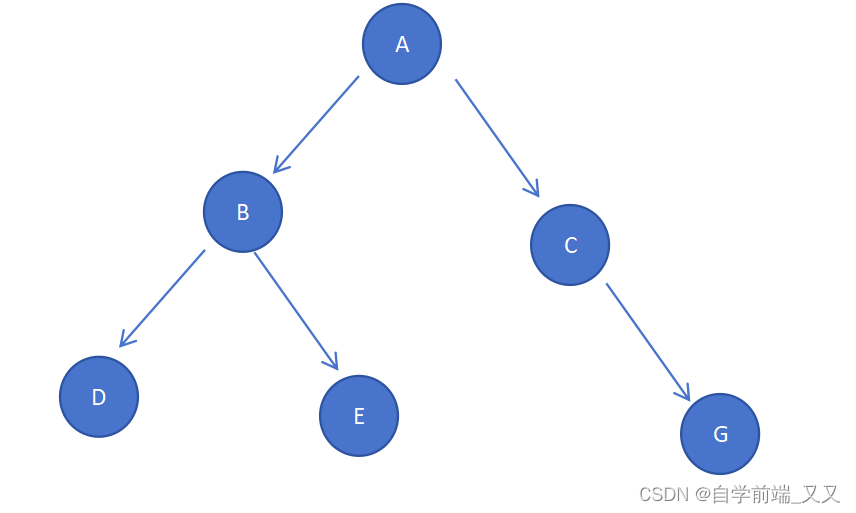
可以使用數組來存儲。但只適用于滿二叉樹和完全二叉樹的情況。否則如果中間缺失了節點，在數組中相應的位置就要空在那里，造成了空間的浪費。之所以F的位置要空在這里，是因為G是C的右子樹，而左子樹是沒有節點的。如果那個位置不空著，則G就表示為左子樹了。這也就是用數組存儲的不好之處了。

鏈式存儲

用鏈表來創建樹結構。注意：此時用鏈表來表示樹，并非說此時的樹就是線性結構。而是用鏈表重新去定義一種數據結構。此時這個結構只能稱作樹，而不可以稱作鏈表。
用鏈表創建樹的好處就是左子樹與右子樹的表示。如上面的示例，直接在每個節點上存儲三個信息：1、數據本身的信息，2、左子樹的指針，3、右子樹的指針。這時G就直接可以表示為C的右子樹，而其左子樹指向NULL。

// 二叉樹節點的結構體定義  
typedef struct TreeNode {  int val;            // 節點的值  struct TreeNode *left;   // 左子樹  struct TreeNode *right;  // 右子樹  
} TreeNode; 

查找方式

對二叉樹的查找有三種方式，是按照查找根的點的順序來區分的。$先序$（根節點、左子樹、右子樹），$中序$（左子樹、根節點、右子樹），$后序$（左子樹、右子樹、根節點）。

前序的訪問順序：A B D E C G
中序的訪問順序：D B E A C G
后序的訪問順序：D E B G C A