常見的排序算法【總結】

- 排序的基本概念與分類
- 排序的穩定性
- 內排序與外排序
- 簡單排序
- - 冒泡排序
  - - 時間復雜度： $O(n^2)$
  - 簡單選擇排序
  - - 排序原理：
    - 時間復雜度： $O(n^2)$
  - 插入排序
  - - 排序原理：
    - 時間復雜度： $O(n^2)$
- 高級排序
- - 希爾排序
  - - 排序原理：
  - 歸并排序
  - - 排序原理：
    - 時間復雜度： $O (n l o g n)$
    - 空間復雜度： $O (N)$
    - 歸并排序的缺點
    - 算法性能
  - 快速排序
  - - 時間復雜度： $O (n l o g n)$
    - 排序原理：
    - 切分原理：
    - 快速排序和歸并排序的區別：
  - 堆排序
  - - 大頂堆和小頂堆
    - 堆排序基本原理：
- 排序算法的選擇

排序的基本概念與分類

排序就是將一組雜亂無章的數據按照一定的規律（升序或降序）組織起來。
在排序問題中，通常將數據元素稱為記錄。可以將排序看成是線性表的一種操作。

排序的穩定性

排序算法	平均時間復雜度	最好情況	最壞情況	空間復雜度	穩定性
冒泡排序	O(n²)	O(n)	O(n²)	O(1)	穩定
簡單選擇排序	O(n²)	O(n²)	O(n²)	O(1)	不穩定
插入排序	O(n²)	O(n)	O(n²)	O(1)	穩定
希爾排序	O(nlogn) ~ O(n²)	O(n^1.3)	O(n²)	O(1)	不穩定
堆排序	O(nlogn)	O(nlogn)	O(nlogn)	O(1)	不穩定
歸并排序	O(nlogn)	O(nlogn)	O(nlogn)	O(n)	穩定
快速排序	O(nlogn)	O(nlogn)	O(n²)	O(logn)~O(n)	不穩定

假定在待排序的記錄序列中，存在多個具有相同的關鍵字的記錄，若經過排序，這些記錄的相對次序保持不變，即在原序列中，r[i]=r[j]，且r[i]在r[j]之前，而在排序后的序列中，r[i]仍在r[j]之前，則稱這種排序算法是穩定的；否則稱為不穩定的。
穩定的：冒泡、插入、歸并；
不穩定：選擇、希爾、快速、堆排序

內部排序：數據元素全部放在內存中的排序。
外排排序：數據元素太多不能同時放在內存中，根據排序過程的要求不能在內外存之間移動數據的排序。

內排序與外排序

內排序是排序整個過程中，待排序的所有記錄全部被放置在內存中。

根據排序過程中借助的主要操作，內排序分為插入排序、交換排序、選擇排序和歸并排序。
外排序是由于排序的記錄個數太多，不能同時放置在內存中，整個排序過程需要在內外存之間多次交換數據才能進行。

簡單排序

冒泡、選擇、插入排序都是簡單排序，最壞情況下的時間復雜度都是 $O(n^2)$ ，二平方階隨著輸入規模的增大，事件成本將急劇上升，所以這些基本排序方法不能處理更大規模的問題。

冒泡排序

冒泡排序（Bubble Sort）是一種交換排序，它的基本思想是：兩兩比較相鄰記錄的關鍵字，如果反序則交換，直到沒有反序的記錄為止。

時間復雜度： $O(n^2)$

C#代碼：

public class Bubble
{/// <summary>/// 正宗的冒泡排序/// </summary>/// <param name="nums"></param>public void BubbleSort(int[] nums){int i, j;for (i = 1; i < nums.Length; i++){for (j = nums.Length - 1; j >= i; j--){if (nums[j] < nums[j - 1]){Swap(nums,j,j-1);}}}}/// <summary>/// 優化后的冒泡排序/// </summary>/// <param name="nums"></param>public void BubbleSort1(int[] nums){int i, j;bool flag = true;for (i = 1; i < nums.Length && flag; i++){flag = false;for (j = nums.Length - 1; j >= i; j--){if (nums[j] < nums[j - 1]){Swap(nums,j,j-1);flag = true;}}}}private void Swap(int[] nums,int i, int j){(nums[i], nums[j]) = (nums[j], nums[i]);}
}

簡單選擇排序

排序原理：

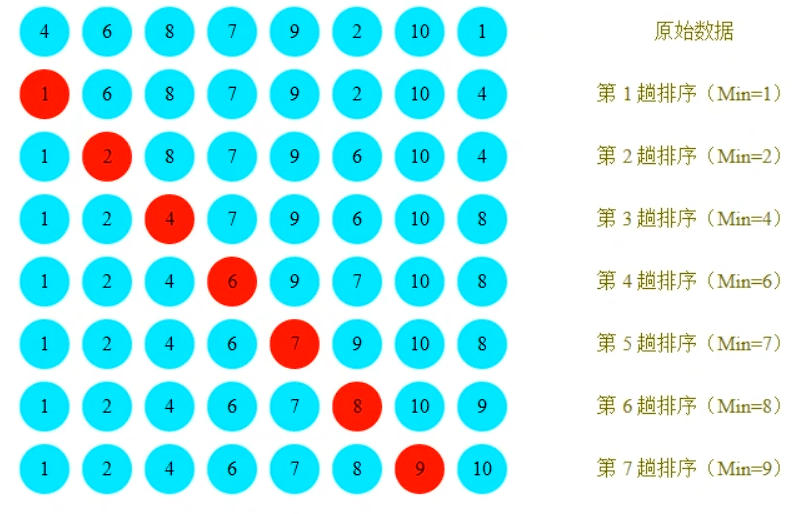
在待排序數組中選出最小的(或最大)的與第一個位置的數據交換然后在剩下的待排序數組中找出最小(或最大)的與第二個位置的數據交換，以此類推，直到第n-1個元素。
簡單選擇排序可以說是冒泡排序的一種改版，它不再兩兩比較出較小數就進行交換，而是每次遍歷比較當前數的后面所有數，最后再把最小的數和當前數進行交換。

時間復雜度： $O(n^2)$

C#代碼：

 public void Select(int[] nums){int min;for (int i = 0; i < nums.Length-1; i++){min = i;for (int j = i+1; j < nums.Length; j++){if (nums[j]<nums[min]){min = j;}}(nums[i], nums[min]) = (nums[min], nums[i]);}}

插入排序

插入排序(Insertion sort)是一種簡單直觀且穩定的排序算法。

插入排序的工作方式非常像人們排序一手撲克牌一樣。開始時，我們的左手為空并且桌子上的牌面朝下。然后，我們每次從桌子上拿走一張牌并將它插入左手中正確的位置。為了找到一張牌的正確位置，我們從右到左將它與已在手中的每張牌進行比較

排序原理：

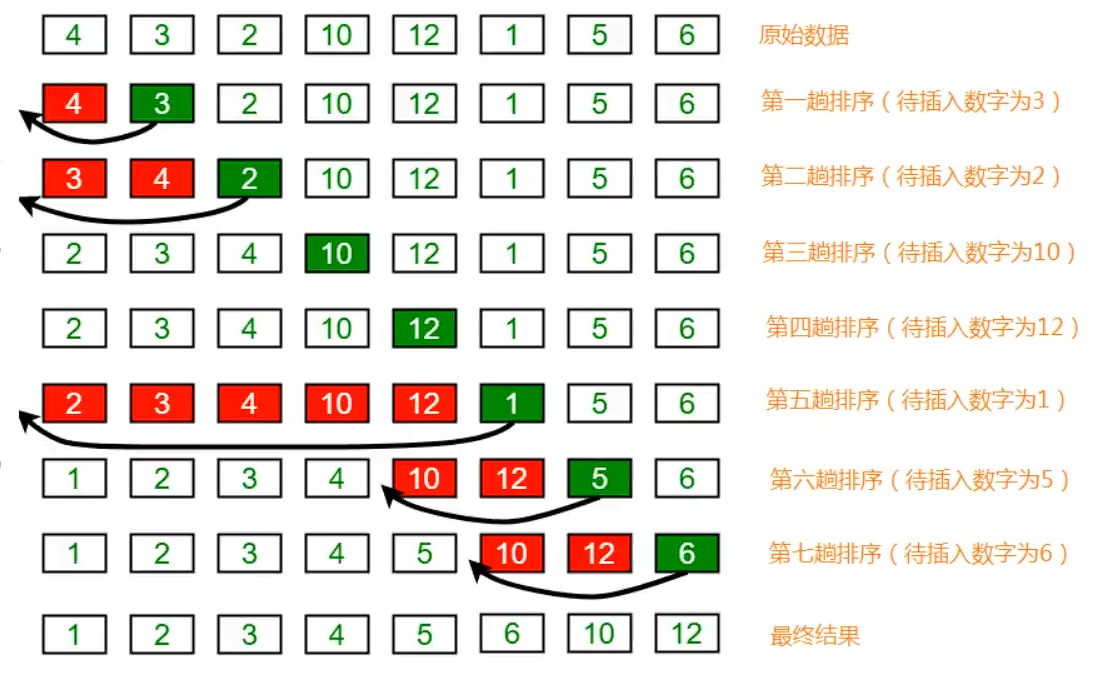
把所有的元素分為兩組，已經排序的和未排序的;
找到未排序的組中的第一個元素，向已經排序的組中進行插入
倒敘遍歷已經排序的元素，依次和待插入的元素進行比較，直到找到一個元素小于等于待插入元素，那么就把待插入元素放到這個位置，其他的元素向后移動一位;

時間復雜度： $O(n^2)$

C#代碼：

public void Insertion(int[] nums){for (int i = 1; i < nums.Length; i++){for (int j = i; j > 0; j--){if (nums[j-1]>nums[j]){//交換元素(nums[j - 1], nums[j]) = (nums[j], nums[j - 1]);}elsebreak;}}}

高級排序

希爾排序

希爾排序是插入排序的一種，又稱“縮小增量排序”,是插入排序算法的一種更高效的改進版本。

前面學習插入排序的時候，我們會發現一個很不友好的事兒，如果已排序的分組元索為{2,5,7,9,10}，未排序的分組元素為{1,8}，那么下一個待插入元素為1，我們需要拿著1從后往前，依次和10,9,7,5,2進行交換位置,才能完成真正的插入,每次交換只能和相鄰的元素交換位置。那如果我們要提高效率，直觀的想法就是一次交換，能把1放到更前面的位置,比如一次交換就能把1插到2和5之間，這樣-次交換1就向前走了5個位置，可以減少交換的次數，這樣的需求如何實現呢?接下來我們來看看希爾排序的原理。

排序原理：

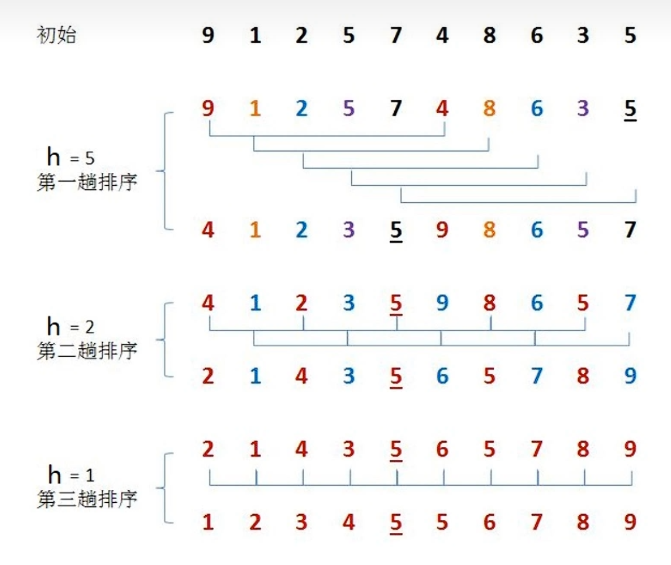
選定一個增長量h，按照增長量h作為數據分組的依據，對數據進行分組
對分好組的每一組數據完成插入排序;
減小增長量，最小減為1,重復第二步操作。
增長量h的確定:我們這里采用以下規則：

int h = 1;
while(h<長度/2)
{h = 2h+1;
}
//循環結束后我們就可以確定h的最大值

h的減小規則為 h = h/2

C#代碼：

public void Shell(int[] nums)
{//確定增長值int h = 1;while (h < nums.Length / 2){h = 2 * h + 1;}while (h>=1){//排序for (int i = h; i < nums.Length; i++){for (int j = i; j >=h ; j-=h){if (nums[j]<nums[j-h]){//交換(nums[j], nums[j - h]) = (nums[j - h], nums[j]);}else{break;}}}h /= 2;}
}

歸并排序

歸并排序是建立在歸并操作上的一種有效的排序算法，該算法是采用分治法的一個非常典型的應用。將已有序的子序列合并，得到完全有序的序列;即先使每個子序列有序，再使子序列段間有序。若將兩個有序表合并成一個有序表,稱為二路歸并。

排序原理：

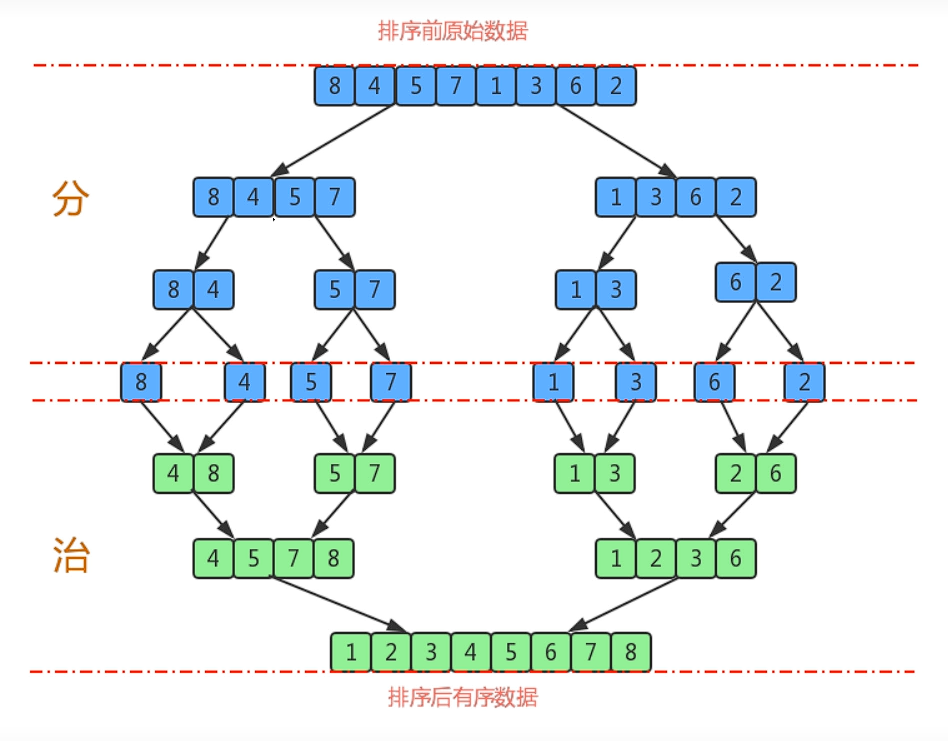
歸并排序算法有兩個基本的操作，一個是分，也就是把原數組劃分成兩個子數組的過程。另一個是治，它將兩個有序數組合并成一個更大的有序數組。

盡可能的一組數據拆分成兩個元素相等的子組，并對每一個子組繼續拆分，直到拆分后的每個子組的元素個數是1為止。
將相鄰的兩個子組進行合并成一個有序的大組;
不斷的重復步驟2，直到最終只有一個組為止。

時間復雜度： $O (n l o g n)$

空間復雜度： $O (N)$

歸并排序需要一個與原數組相同長度的數組做輔助來排序。

歸并排序的缺點

需要申請額外的數組空間，導致空間復雜度提升，是典型的以空間換時間的操作

算法性能

速度僅次于快速排序。

C#代碼：

//遞歸實現的歸并排序
public class MergeSort
{private int[] list;private bool Less(int[] nums,int a, int b){return nums[a] - nums[b] < 0;}public void Sort(int[] nums){int lo = 0;int hi = nums.Length - 1;list = new int[nums.Length];Sort(nums,lo,hi);}private void Sort(int[] nums, int lo, int hi){//安全性校驗if (lo>=hi){return;}int mi = lo + (hi - lo) / 2;//分別對每一組數據進行排序Sort(nums,lo,mi);Sort(nums, mi+1, hi);//把兩個數組進行歸并Merge(nums,lo,mi,hi);}private void Merge(int[] nums, int lo, int mi, int hi){//定義3個指針int p1 = lo;int p2 = mi + 1;int p = lo;//編歷，移動p1指針和p2指針，比較對應索引處的值，找出小的那個，放到輔助數組的對應索引處while (p1 <= mi && p2 <= hi){if (Less(nums,p1,p2)){list[p++] = nums[p1++];}else{list[p++] = nums[p2++];}}//如果p1指針沒有走完while (p1<=mi){list[p++] = nums[p1++];}//如果p2指針沒有走完while (p2<=hi){list[p++] = nums[p2++];}//把輔助數組中的數據拷貝到原數組中for (int i = lo; i <= hi; i++){nums[i] = list[i];}}
}

快速排序

快速排序是對冒泡排序的一種改進。它的基本思想是:通過一趟排序將要排序的數據分割成獨立的兩部分，其中一部分的所有數據都比另外一部分的所有數據都要小，然后再按此方法對這兩部分數據分別進行快速排序，整個排序過程可以遞歸進行，以此達到整個數據變成有序序列。

時間復雜度： $O (n l o g n)$

排序原理：

首先設定一個分界值，通過該分界值將數組分成左右兩部分;
將大于或等于分界值的數據放到到數組右邊,小于分界值的數據放到數組的左邊。此時左邊部分中各元素都小于或等于分界值，而右邊部分中各元素都大于或等于分界值;
然后,左邊和右邊的數據可以獨立排序。對于左側的數組數據，又可以取一個分界值，將該部分數據分成左右兩部分，同樣在左邊放置較小值，右邊放置較大值。右側的數組數據也可以做類似處理。
重復上述過程，可以看出，這是一個遞歸定義。通過遞歸將左側部分排好序后，再遞歸排好右側部分的順序。當左側和右側兩個部分的數據排完序后，整個數組的排序也就完成了

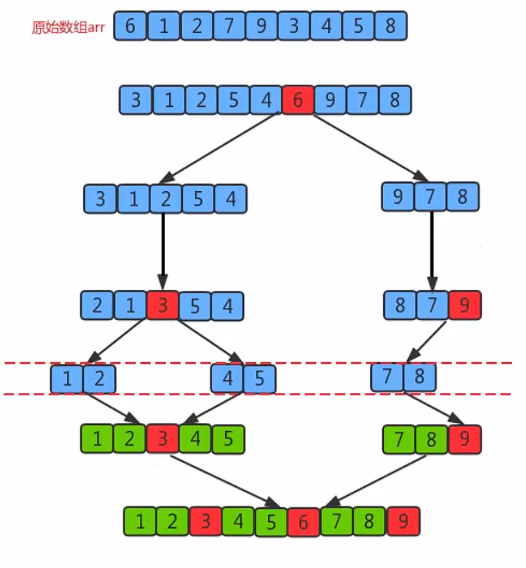
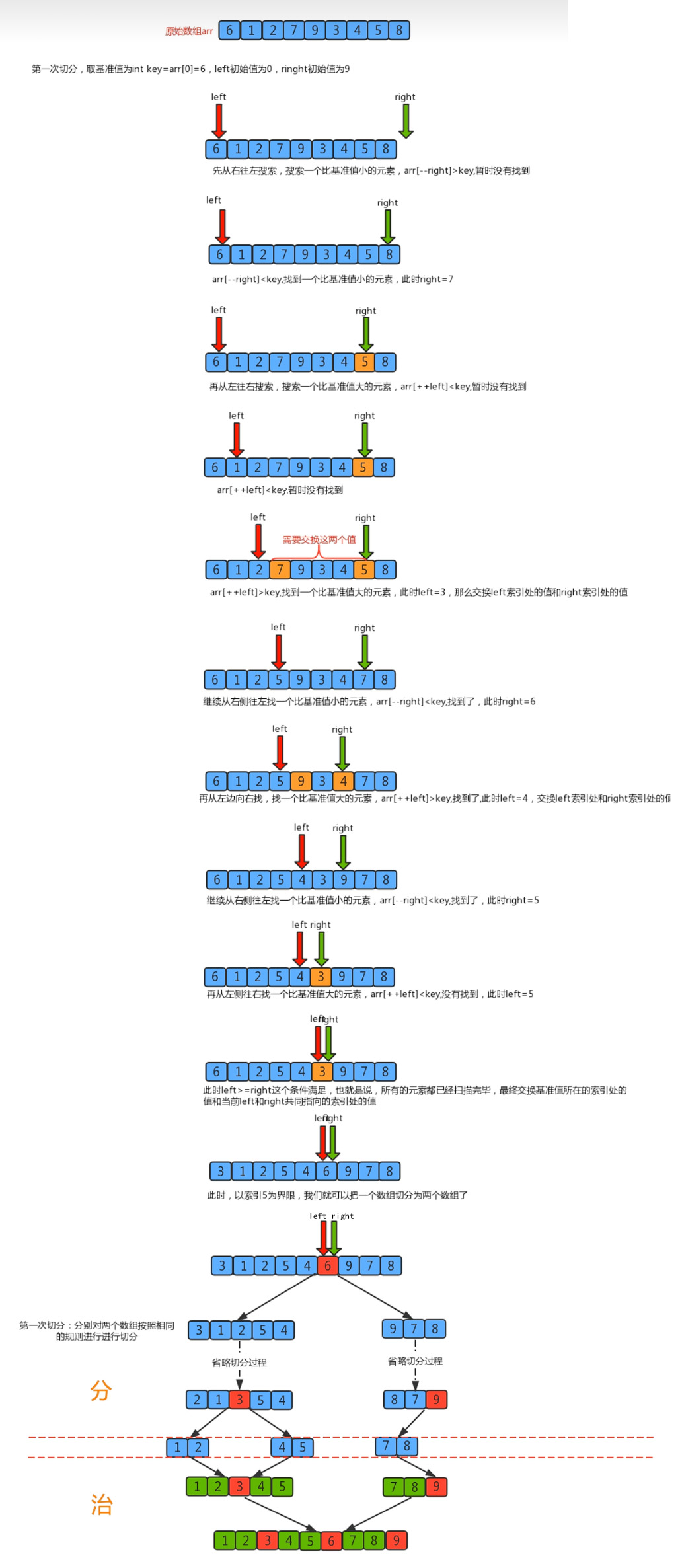
切分原理：

把一個數組切分成兩個子數組的基本思想

找一個基準值，用兩個指針分別指向數組的頭部和尾部
先從尾部向頭部開始搜索一個比基準值小的元素，搜索到即停止，并記錄指針的位置
再從頭部向尾部開始搜索一個比基準值大的元素，搜索到即停止，并記錄指針的位置
交換當前左邊指針位置和右邊指針位置的元素
重復2,3,4步驟，直到左邊指針的值大于右邊指針的值停止。

C#代碼：

//快速排序主要有三個參數，left 為區間的開始地址，right 為區間的結束地址，Key 為當前的開始的值。
//我們從待排序的記錄序列中選取一個記錄（通常第一個）作為基準元素（稱為key）key=arr[left]，然后設置兩個變量，left指向數列的最左部，right 指向數據的最右部。
public class QuickSort
{public void Sort(int[] arr){Quick(arr, 0, arr.Length - 1);}private void Quick(int[] arr, int left, int right){if (left < right){int pivot = Partition(arr, left, right);Quick(arr, left, pivot - 1);Quick(arr, pivot + 1, right);}}private int Partition(int[] arr, int left, int right){int pivotKey = arr[left];while (left < right){while (left < right && arr[right] >= pivotKey){right--;}arr[left] = arr[right];while (left < right && arr[left] <= pivotKey){left++;}arr[right] = arr[left];}arr[left] = pivotKey;return left;}
}

快速排序和歸并排序的區別：

快速排序是另外一種分治的排序算法，它將一個數組分成兩個子數組，將兩部分獨立的排序。快速排序和歸并排序是互補的:歸并排席將數組分成兩個子數組分別排序，并將有序的子數組歸并從而將整個數組排序，而快速排序的方式則是當兩個數組都有序時，整個數組自然就有序了。在歸并排序中，一個數組被等分為兩半,歸并調用發生在處理整個數組之前，在快速排序中，切分數組的位置取決于數組的內容，遞歸調用發生在處理整個數組之后。

堆排序

堆排序相當于簡單選擇排序的升級，他們同屬于選擇排序類。堆的結構可以分為大頂堆和小頂堆，是一個完全二叉樹，而堆排序是根據堆的這種數據結構設計的一種排序。

大頂堆和小頂堆

性質：每個結點的值都大于或等于其左孩子和右孩子結點的值，稱之為大頂堆；每個結點的值都小于或等于其左孩子和右孩子結點的值，稱之為小頂堆。如下圖

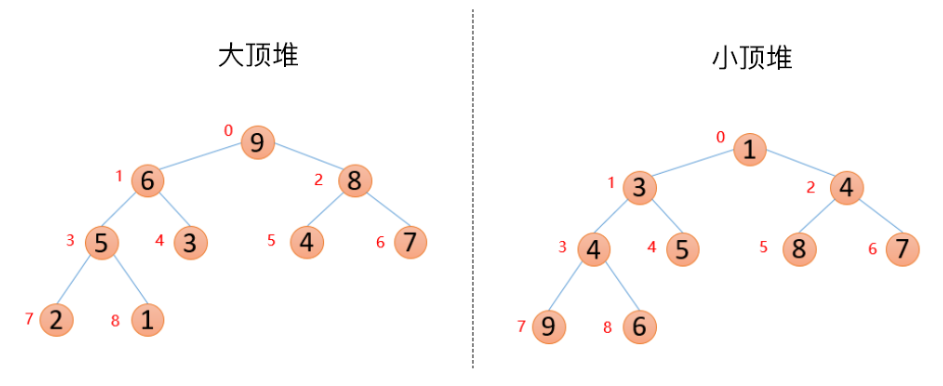
上面的結構映射成數組

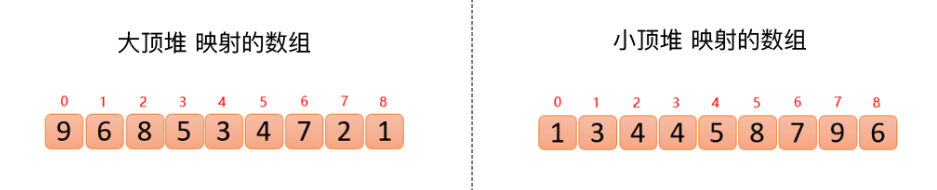
查找數組中某個數的父結點和左右孩子結點，比如已知索引為i的數，那么

1.父結點索引：(i-1)/2（這里計算機中的除以2，省略掉小數）

2.左孩子索引：2*i+1

3.右孩子索引：2*i+2

所以上面兩個數組可以腦補成堆結構，因為他們滿足堆的定義性質：

大頂堆：arr(i)>arr(2*i+1) && arr(i)>arr(2*i+2)

小頂堆：arr(i)<arr(2*i+1) && arr(i)<arr(2*i+2)

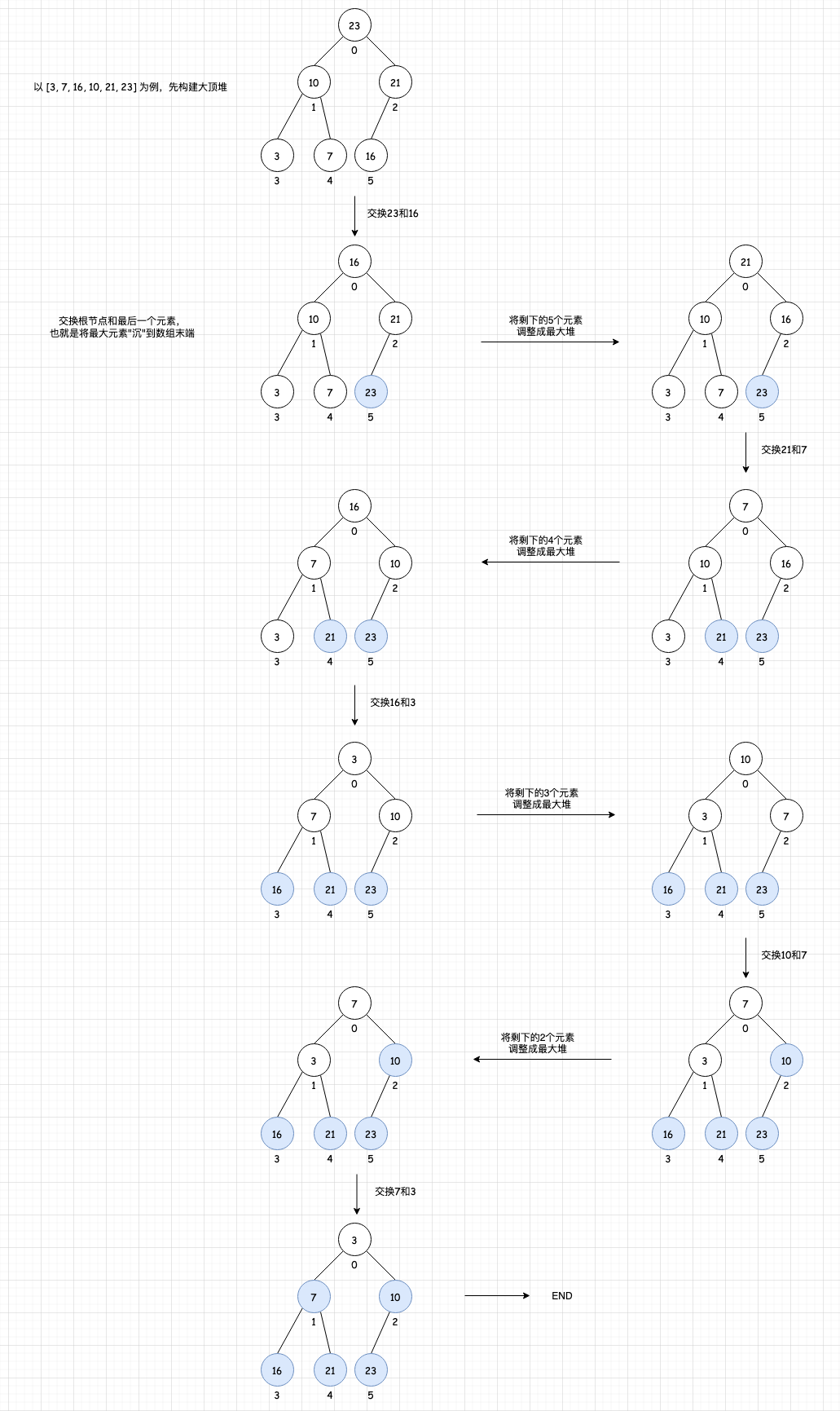
堆排序基本原理：

首先將待排序的數組構造成一個大頂堆，此時，整個數組的最大值就是堆結構的頂端
將頂端的數與末尾的數交換，此時，末尾的數為最大值，剩余待排序數組個數為n-1
將剩余的n-1個數再構造成大根堆，再將頂端數與n-1位置的數交換，如此反復執行，便能得到有序數組

C#代碼：

public class HeapSort  
{  public static void Sort(int[] arr)  {  int n = arr.Length;  // 構建最大堆：大頂堆的構建過程就是從最后一個非葉子結點開始從下往上調整,則最后一個非葉子結點的位置是：數組長度/2-1。  for (int i = n / 2 - 1; i >= 0; i--)  Heapify(arr, n, i);  // 排序for (int i = n - 1; i >= 0; i--)  {  // 將當前最大的元素 arr[0] 和 arr[i] 交換  Swap(arr, 0, i);  // 重新調整剩余元素為最大堆  Heapify(arr, i, 0);  }  }  // 調整以 pos 為根的子樹，使其保持最大堆的性質  private static void Heapify(int[] arr, int n, int pos)  {  int largest = pos; // 初始化 largest 為根  int left = 2 * pos + 1; // 左子節點  int right = 2 * pos + 2; // 右子節點  // 如果左子節點比根大  if (left < n && arr[left] > arr[largest])  largest = left;  // 如果右子節點比當前最大的還大  if (right < n && arr[right] > arr[largest])  largest = right;  // 如果最大的不是根  if (largest != pos)  {  // 交換  Swap(arr, pos, largest);  // 遞歸地調整受影響的子樹  Heapify(arr, n, largest);  }  }  // 交換數組中的兩個元素  private static void Swap(int[] arr, int i, int j)  {  (arr[i], arr[j]) = (arr[j], arr[i]);  }  
}