一、樹的基本概念

1、樹的簡介

之前我們都是在談論一對一的線性數據結構，可現實中也有很多一對多的情況需要處理，所以我們就需要一種能實現一對多的數據結構--“樹”。

2、樹的定義

樹（Tree）是一種非線性的數據結構，它是n(n >= 0)個結點組成的一個具有層次關系的有限集。之所以把它叫做樹是因為它看起來像一顆倒掛的樹，也就是它的根是朝上，而葉子是朝上的。

在n=0時稱為空樹。在任意一顆非空樹中：

1. 有且僅有一個特定的稱為根(Root)的結點；
2. 當n>1時，其余結點可分為m(m > 0)個互不相交的有限集T1、T2、...... 、Tm，其中每一個集合本身又是一棵樹，并且稱為根的子樹(SubTree)。

注意：在樹型結構中，子樹之間不能有交集，否則就不能是樹形結構。?如果相交了，那就是圖。

3、樹的一些基本術語

就拿這張圖來舉例子

1. 節點的度：一個節點含有的子樹的個數稱為該節點的度； 如上圖：A的為6
2. 葉節點或終端節點：度為0的節點稱為葉節點； 如上圖：B、C、H、I...等節點為葉節點
3. 非終端節點或分支節點：度不為0的節點； 如上圖：D、E、F、G...等節點為分支節點
4. 雙親節點或父節點：若一個節點含有子節點，則這個節點稱為其子節點的父節點； 如上圖：A是B的父節點
5. 孩子節點或子節點：一個節點含有的子樹的根節點稱為該節點的子節點； 如上圖：B是A的孩子節點
6. 兄弟節點：具有相同父節點的節點互稱為兄弟節點； 如上圖：B、C是兄弟節點
7. 樹的度：一棵樹中，最大的節點的度稱為樹的度； 如上圖：樹的度為6
8. 節點的層次：從根開始定義起，根為第1層，根的子節點為第2層，以此類推；
9. 樹的高度或深度：樹中節點的最大層次； 如上圖：樹的高度為4
10. 堂兄弟節點：雙親在同一層的節點互為堂兄弟；如上圖：H、I互為兄弟節點
11. 節點的祖先：從根到該節點所經分支上的所有節點；如上圖：A是所有節點的祖先
12. 子孫：以某節點為根的子樹中任一節點都稱為該節點的子孫。如上圖：所有節點都是A的子孫
13. 森林：由m（m>0）棵互不相交的樹的集合稱為森林；

---

二、樹的存儲結構

提及存儲結構，那必然會想到兩種常用的存儲結構。一個是順序存儲結構，另一個則是鏈式存儲結構。這兩個存儲結構在我們之前學習其他的數據結構中也學習過。

樹結構相對線性表就比較復雜了，要存儲表示起來就比較麻煩了，既要保存值域，也要保存結點和結點之間的關系。實際中樹有很多種表示方式如：雙親表示法，孩子表示法、孩子雙親表示法以及孩子兄弟表示法等。我們這里就簡單的了解雙親表示法，孩子表示法以及孩子兄弟表示法。

1、雙親表示法

我們人可能因為種種原因，沒有孩子，但無論是誰都不可能是從石頭里蹦出來的（孫悟空除外，它顯然不算是人），所以人一定就會有父母。樹這種結構也不例外，除了根結點外，其余的每個結點不一定有孩子，但一定有且一個雙親。

#define MAX_TREE_SIZE 100typedef int TElemType;              //樹結點的數據類型，目前暫定為整形typedef struct PTNode
{TElemType data;                //結點數據int parent;                    //雙親位置
}PTNode;typedef struct
{PTNode nodes[MAX_TREE_SIZE];    //結點數組    int r,n;                        //根的位置和結點數
}

這樣的存儲結構，我們根據結點的?parent指針很容易找到它的雙親結點，所用的時間復雜度為O(1)。但麻煩的是如果想要知道結點的孩紙是誰，不好意思，請遍歷整個結構才行。

2、孩子表示法

把每個結點的孩子結點排列起來，以單鏈表作為存儲結構，則n個結點有n個孩子鏈表，如果是葉子結點則此單鏈表為空。然后n個頭指針又組成一個線性表，采用順序存儲結構，存放進一個一維數組中。

?

為此，需要設計兩種結點結構，一個是孩子鏈表的孩子結點，如下表所示

其中，child是數據域，用來存儲某個結點在表頭數組中的下標；next是指針域，用來存儲指向某個結點的下一個孩子結點的指針。

另一個是表頭數組的表頭結點，如下表所示

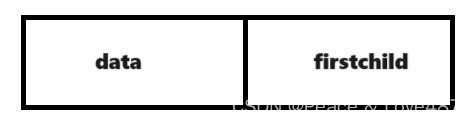
其中，data是數據域，存儲某個結點的數據信息；firstchild是頭指針域，存儲該結點的孩子鏈表的頭指針。

#define max_TREE_SIZE 100typedef int TElemType;                //樹結點的數據類型，目前暫定為整形typedef struct CTNode                 //孩子結點
{int child;struct CTNode* next;    
} *ChildPtr;typedef strucct                        //表頭結構
{TElemType data;ChildPTr firstchild;
}CTBox;typedef struct                         //樹結構
{CTBox nodes[MAX_TREE_SIZE];        //結點數組int r,n;                           //結點位置和結點數
}CTree;

?這樣的數據結構對于我們要查找某個結點的孩子，或者找某個結點的兄弟，只需要查找這個結點的孩子單鏈表即可。對于遍歷整棵樹也是很方便的，對頭結點的數組循環即可。

但是如果想知道某個結點的雙親是誰？就需要遍歷整棵樹。所以就衍生出了將二者合二為一的方法：孩子兄弟表示法。

3、孩子兄弟表示法

typedef int DataType;
struct Node
{struct Node* _firstChild1; // 第一個孩子結點struct Node* _pNextBrother; // 指向其下一個兄弟結點DataType _data; // 結點中的數據域
};

?這種表示法，給查找某個結點的某個孩子帶來了方便，只需要通過firstchild找到此結點的長子，然后通過長子結點的nextbrother找到它的二弟，接著一直下去，直到找到具體的孩子。

三、樹在實際中的運用(表示文件系統的目錄樹結構)

---

以上就是關于樹的基本概念和存儲結構的知識點。有關二叉樹的內容會在下一個章節中再詳細描述。