前兩天有小伙伴說想要把常見算法的原理 + 公式匯集起來。
這樣非常非常方便查看!分為上下兩篇,下篇地址:
本次文章分別從下面6個方面,涉及到20個算法知識點:
-
監督學習算法
-
無監督學習算法
-
半監督學習算法
-
強化學習算法
-
集成學習算法
-
深度學習算法
監督學習算法
監督學習算法是一種通過學習輸入數據和相應的標簽之間的關系來進行預測或分類的方法。
在監督學習中,模型接收帶有標簽的訓練數據,然后通過學習這些數據的模式來進行預測或分類新的未標記數據。
1、線性回歸
線性回歸是一種用于建立和分析變量之間線性關系的監督學習算法。它主要用于解決回歸問題,即預測一個或多個連續數值型輸出(因變量)與一個或多個輸入特征(自變量)之間的關系。
基本原理
線性回歸基于一個簡單的假設,即因變量(輸出)與自變量(輸入)之間存在線性關系。這意味著我們假設輸出可以通過輸入的線性組合來預測,其中每個輸入特征都與一個權重相乘,然后將它們相加,再加上一個截距(常數項)。
核心公式
考慮一個簡單的線性回歸問題,其中有一個自變量(特征)x和一個因變量(輸出)y。線性回歸的基本公式可以表示為: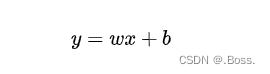
2、邏輯回歸
邏輯回歸是一種用于解決二分類問題的監督學習算法,其基本原理是使用邏輯函數(也稱為Sigmoid函數)來建模因變量(輸出)與自變量(輸入)之間的概率關系。邏輯回歸的目標是估計某個事件發生的概率,通常表示為0或1,例如腫瘤是惡性(1)或良性(0)。
基本原理
邏輯回歸基于以下思想:我們希望將線性組合的輸出映射到一個介于0和1之間的概率值,以表示事件發生的可能性。為此,邏輯回歸使用邏輯函數(Sigmoid函數)來執行這種映射。
核心公式
邏輯回歸的核心公式可以表示為: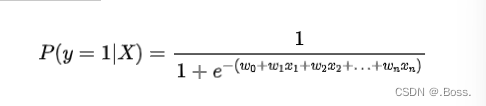
3、決策樹
決策樹是一種常用的監督學習算法,用于解決分類和回歸問題。它的基本原理是根據數據的特征來構建一顆樹狀結構,樹的每個節點代表一個特征,每個分支代表一個特征的取值,葉節點代表輸出類別或數值。決策樹的目標是通過分裂特征,將數據集劃分為純度更高的子集,以最小化誤差或不純度。
基本原理
決策樹的基本原理是根據一系列的規則來做出決策。這些規則是通過對輸入特征進行分裂來確定的,每次分裂都會將數據集劃分為更加純凈的子集。決策樹的構建過程通常分為以下幾個步驟:
1、選擇一個用于分裂的特征,通常是根據某種度量標準(如信息增益、基尼不純度等)來選擇的,以確保分裂后子集的純度更高。
2、根據選定的特征和分裂點將數據集劃分為子集。
3、遞歸地應用步驟1和步驟2,直到滿足停止條件(如樹的深度達到預定值、子集的大小小于某個閾值等)。
4、在葉節點上分配一個輸出標簽(分類問題)或數值(回歸問題),通常是該葉節點中樣本的多數類別或均值。
涉及公式
決策樹并不涉及像線性回歸或邏輯回歸那樣的具體數學公式,而是通過樹的結構來進行決策。然而,有一些用于分裂特征的評估標準,其中最常見的是基尼不純度和信息增益。這些標準用于選擇最佳的分裂點,從而構建更好的決策樹。
1、基尼不純度(Gini Impurity):用于分類問題,表示從數據集中隨機選擇一個樣本,該樣本被誤分類的概率。基尼不純度越低,表示數據集的純度越高。它的數學公式為:
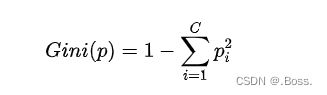
2、信息增益(Information Gain):也用于分類問題,表示在某個特征上進行分裂后,熵(entropy)減少的程度,即數據集的不確定性減少的程度。信息增益越高,表示特征分裂后數據更加純凈。
它的數學公式為: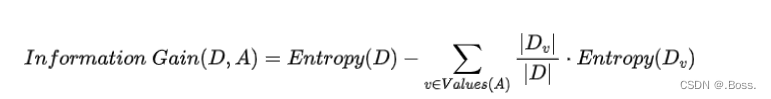
決策樹的訓練過程旨在最大化信息增益或最小化基尼不純度,以選擇最佳的分裂點。一旦構建好了決策樹,就可以使用它來進行分類或回歸預測。決策樹易于理解和可視化,但在某些情況下可能容易過擬合數據,因此通常需要通過剪枝等技術來提高泛化性能。
4、支持向量機
支持向量機(Support Vector Machine,SVM)是一種強大的監督學習算法,主要用于分類問題,但也可用于回歸和異常檢測。SVM的基本原理是在特征空間中找到一個最優的超平面,以最大化不同類別之間的間隔,從而使分類更加準確。
基本原理
1、間隔最大化:SVM的目標是找到一個超平面,使不同類別的樣本點到這個超平面的距離(間隔)最大化。這個間隔被稱為“間隔最大化”。
2、支持向量:在SVM中,只有一小部分樣本點對超平面的位置具有影響力,它們被稱為“支持向量”。這些支持向量是距離超平面最近的樣本點,它們決定了超平面的位置。
3、核技巧:SVM還使用了核函數,可以將數據從原始特征空間映射到一個更高維度的特征空間。這使得SVM可以處理非線性可分的數據。
核心公式
在SVM中,核心公式涉及到以下關鍵概念:
1、決策函數:用于將輸入特征向量映射到超平面并進行分類。決策函數的基本形式如下:
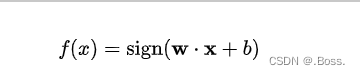
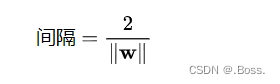
2、間隔:SVM的目標是最大化間隔,其中間隔定義為支持向量到超平面的距離的兩倍。支持向量到超平面的距離可以用以下公式表示:
5、K最近鄰
K最近鄰(K-Nearest Neighbors,簡稱KNN)是一種常用的監督學習算法,主要用于分類和回歸問題。KNN的基本原理是基于特征空間中樣本點的距離來進行預測或分類。
對于分類問題,KNN找到與待分類樣本在特征空間中最近的K個訓練樣本,并基于它們的類別標簽進行投票決策。對于回歸問題,KNN找到最近的K個訓練樣本,并計算它們的平均值或加權平均值來預測待預測樣本的數值輸出。
基本原理
1、距離度量:KNN基于樣本點之間的距離來度量它們的相似性。通常使用歐幾里德距離、曼哈頓距離、閔可夫斯基距離等來計算距離。
2、K值選擇:KNN中的K表示選擇最近鄰的數量。通過選擇不同的K值,可以調整模型的復雜性。較小的K值可能會導致模型對噪聲敏感,而較大的K值可能會導致模型過于平滑。
3、投票或平均:對于分類問題,KNN對最近的K個訓練樣本的類別標簽進行投票,然后將得票最多的類別標簽分配給待分類樣本。對于回歸問題,KNN計算最近的K個訓練樣本的數值輸出的平均值或加權平均值,并將結果用作待預測樣本的輸出。
核心公式
KNN的核心公式涉及到距離度量和K個最近鄰的選擇。
1、距離度量:KNN使用距離度量來計算樣本之間的距離。對于兩個樣本點??和?,歐幾里德距離的計算公式為:

2、K個最近鄰的選擇:對于分類問題,KNN選擇與待分類樣本距離最近的K個訓練樣本,然后根據它們的類別標簽進行投票決策。對于回歸問題,KNN選擇與待預測樣本距離最近的K個訓練樣本,然后計算它們的數值輸出的平均值或加權平均值來預測。
KNN是一種簡單而直觀的算法,它不需要訓練過程,但在處理大規模數據集時可能會變得計算密集。選擇合適的距離度量和K值是KNN的關鍵,通常需要根據具體問題進行調整和優化。
此外,KNN在處理不平衡數據和高維數據時可能會表現不佳,因此需要謹慎選擇適用場景。
無監督學習算法
無監督學習算法是從未標記的數據中自動發現隱藏的模式和結構,而無需事先提供標簽或目標。
1、K均值聚類
K 均值聚類(K-Means Clustering)是一種常見的無監督學習算法,用于將數據集劃分為K個不同的簇(cluster),使得每個數據點屬于距離其最近的簇的中心點。
K均值聚類的基本原理是通過迭代優化,將數據點分配給簇并更新簇的中心點,以最小化每個數據點到其所屬簇中心點的距離平方和(稱為“簇內平方和”或“Inertia”)。
基本原理
1、隨機初始化:首先,隨機選擇K個數據點作為初始簇中心點。
2、分配數據點:對于每個數據點,計算其與各個簇中心點的距離,并將其分配到距離最近的簇中心點所屬的簇。
3、更新簇中心點:對于每個簇,計算該簇內所有數據點的平均值,將其作為新的簇中心點。
4、重復迭代:重復步驟2和步驟3,直到簇中心點不再發生明顯變化,或者達到預定的迭代次數。
K均值聚類的目標是最小化以下損失函數(簇內平方和):
K均值聚類的結果是將數據點劃分為K個簇,并且每個簇由一個中心點表示。這個算法通常需要多次運行,并在不同的初始簇中心點選擇下進行迭代,以找到全局最優解。K均值聚類是一種簡單而有效的聚類算法,但它對初始簇中心點的選擇敏感,并且需要指定K的值。
2、主成分分析
主成分分析(Principal Component Analysis,PCA)是一種常用的降維技術和數據分析方法,用于減少數據集的維度,同時保留數據中的主要信息。PCA的基本原理是通過線性變換將高維數據投影到一個低維的子空間,以找到最大方差的方向,這些方向被稱為主成分。
基本原理
1、數據中心化:首先,對原始數據進行中心化處理,即將每個特征的均值減去每個數據點的對應特征值,以確保數據的均值為零。
2、協方差矩陣:然后,計算數據的協方差矩陣,該矩陣表示了不同特征之間的關聯性。
3、特征值分解:對協方差矩陣進行特征值分解,找到其特征值和特征向量。
4、選擇主成分:選擇具有最大特征值的特征向量,這些特征向量構成了數據在低維子空間上的新坐標軸,被稱為主成分。
5、投影:將原始數據投影到所選的主成分上,從而實現數據的降維。
核心公式
1、數據中心化:對于一個包含m個樣本和n個特征的數據矩陣X,首先計算每個特征的均值,然后進行中心化處理,得到中心化的數據矩陣X:
3、高斯混合模型
高斯混合模型(Gaussian Mixture Model,GMM)是一種概率模型,用于對多個高斯分布組合來建模數據分布。它在許多領域中都有廣泛的應用,包括聚類、密度估計、異常檢測等。GMM的基本原理是假設數據是由多個高斯分布組合而成,每個高斯分布被稱為一個組件。以下是GMM的基本原理和核心公式:
基本原理
1、高斯分布的線性組合:GMM假設數據是由K個高斯分布組合而成的,其中K是用戶定義的分量數量。每個高斯分布被稱為一個組件,表示數據在不同區域的概率密度。
2、隱變量:每個數據點都與一個隱變量相關聯,這個隱變量表示數據點屬于哪個組件。通常,這個隱變量是一個離散的變量,取值范圍為1到K。
3、生成數據的過程:生成一個數據點的過程如下:
-
首先,選擇一個組件(隱變量的取值),確定數據點屬于哪個高斯分布。
-
然后,根據選定的組件的高斯分布生成具體的數據點。
4、參數估計:通過最大似然估計等方法,估計每個組件的均值、方差和混合系數,以擬合數據。
核心公式
1、高斯分布的概率密度函數:高斯分布的概率密度函數是GMM的核心組成部分,表示了數據在每個組件上的分布。對于一維高斯分布,概率密度函數為:
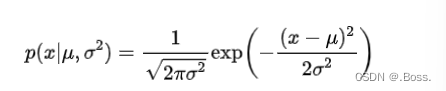
2、GMM的概率密度函數:GMM的概率密度函數是多個高斯分布的線性組合,表示了數據在整個模型上的分布。對于一維數據,GMM的概率密度函數為:
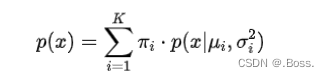
4、層次聚類
層次聚類(Hierarchical Clustering)是一種基于數據相似性的聚類算法,它的基本原理是通過不斷地合并或分割數據點,創建一個層次化的聚類結構。
層次聚類可分為兩種主要類型:凝聚型(Agglomerative)和分裂型(Divisive)。凝聚型聚類從每個數據點作為一個單獨的簇開始,然后逐漸合并相似的簇,直到所有數據點都屬于一個大簇。分裂型聚類則從所有數據點屬于一個大簇開始,然后逐漸分割簇,直到每個數據點都成為一個單獨的簇。
基本原理
1、初始狀態:將每個數據點視為一個單獨的簇,形成初始的N個簇,其中N是數據點的數量。
2、相似性度量:計算每對簇之間的相似性,通常使用距離度量(如歐幾里德距離、曼哈頓距離、相關性等)來度量簇內數據點之間的差異。
3、合并最相似的簇:選擇最相似的兩個簇,將它們合并成一個新的簇。合并的規則通常包括單鏈接(single linkage)、完全鏈接(complete linkage)、平均鏈接(average linkage)等。
4、重復合并:重復步驟3,繼續合并最相似的簇,直到只剩下一個簇,或者滿足預定的停止條件(如簇的數量等)。
涉及公式
層次聚類沒有明確的核心數學公式,因為它的操作涉及到相似性度量和合并規則的選擇,這些規則會影響聚類的結果。
1、相似性度量:通常使用距離度量來計算兩個簇之間的相似性。例如,兩個簇A和B之間的距離可以使用歐幾里德距離表示:
其中,和是兩個簇內的數據點的特征值。
2、合并規則:選擇合并兩個簇的規則會影響聚類的結果。例如,單鏈接合并規則下,兩個簇之間的距離通常是兩個簇內距離最近的數據點之間的距離。完全鏈接合并規則下,兩個簇之間的距離通常是兩個簇內距離最遠的數據點之間的距離。
3、樹狀圖(Dendrogram):層次聚類的結果通常表示為一棵樹狀圖,樹的每個節點代表一個簇或合并的簇,葉子節點代表單個數據點。樹狀圖可以用于選擇合適的聚類數量。
層次聚類的優點包括不需要事先指定聚類數量,結果可以以層次化的方式展示數據之間的相似性,但它的計算復雜度相對較高。選擇合適的相似性度量和合并規則以及聚類數量是層次聚類中的關鍵問題。
5、自編碼器(Autoencoders)
自編碼器(Autoencoder)是一種神經網絡架構,用于無監督學習和特征學習。它的基本原理是通過學習數據的緊湊表示(編碼),然后再從該編碼中重建原始數據,從而可以用來提取數據的關鍵特征、降低數據維度、去噪以及生成新數據。自編碼器通常由兩部分組成:編碼器(Encoder)和解碼器(Decoder)。
基本原理
1、編碼器(Encoder):編碼器將輸入數據映射到低維度的編碼空間,通常通過一系列神經網絡層來實現。編碼器的目標是將輸入數據壓縮到一個緊湊的表示,捕獲數據的關鍵特征。
2、解碼器(Decoder):解碼器將編碼后的表示映射回原始數據空間,也通常通過一系列神經網絡層來實現。解碼器的目標是從編碼中重建盡可能接近原始數據的輸出。
3、重建損失(Reconstruction Loss):自編碼器的訓練過程包括最小化輸入數據與解碼器輸出之間的重建損失,通常使用均方差(Mean Squared Error,MSE)作為損失函數。重建損失衡量了重建數據與原始數據之間的差異,促使自編碼器學習捕捉數據的重要特征。
4、降維和特征學習:自編碼器可以用來實現數據降維,通過減小編碼的維度,從而提取數據的關鍵特征。編碼器的隱藏層表示可以被視為數據的壓縮表示。
核心公式
自編碼器的核心公式涉及到編碼和解碼過程,以及重建損失的計算。
1、編碼過程:編碼器將輸入數據??映射到編碼表示?,可以表示為: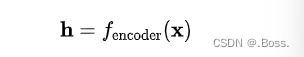
未完待續。。

)




拆分大項目 — 概述及使用要求,執行過程及其實現,替代解決方案 ~)




![[muduo網絡庫]——使用muduo庫搭建Echo服務器(剖析muduo網絡庫核心部分、設計思想)](http://pic.xiahunao.cn/[muduo網絡庫]——使用muduo庫搭建Echo服務器(剖析muduo網絡庫核心部分、設計思想))

)






