1.組合總和

題目鏈接/文章講解： 代碼隨想錄

視頻講解：帶你學透回溯算法-組合總和（對應「leetcode」力扣題目：39.組合總和）| 回溯法精講！_嗶哩嗶哩_bilibili

代碼：（未剪枝版 ）

class Solution {
private:vector<int> path;vector<vector<int>> result;void backtracking(vector<int>& candidates,int target,int startIndex){// 遞歸出口if(target < 0){return;}if(target == 0){result.push_back(path);return;}// 處理結點for(int i = startIndex;i < candidates.size();i++){target -= candidates[i];path.push_back(candidates[i]);backtracking(candidates,target,i);path.pop_back();target += candidates[i];}}
public:vector<vector<int>> combinationSum(vector<int>& candidates, int target) {if(candidates.size() == 0) return result;backtracking(candidates,target,0);return result;}
};

?代碼：（剪枝版）

class Solution {
private:vector<int> path;vector<vector<int>> result;void backtracking(vector<int>& candidates,int target,int startIndex){// 遞歸出口if(target < 0){return;}if(target == 0){result.push_back(path);return;}// 處理結點// 這里加了判斷：如果下一輪的target已經小于0了，就沒有必要遞歸了for(int i = startIndex;i < candidates.size() && target - candidates[i] >= 0;i++){target -= candidates[i];path.push_back(candidates[i]);backtracking(candidates,target,i);path.pop_back();target += candidates[i];}}
public:vector<vector<int>> combinationSum(vector<int>& candidates, int target) {if(candidates.size() == 0) return result;sort(candidates.begin(), candidates.end()); // 涉及大小的剪枝必排序backtracking(candidates,target,0);return result;}
};

思路：學到了這種元素數量不限制的取的解法

其實startIndex變量還是要有，因為我們求的是組合，要數層去重；并且這是在同一個數組里取數。

而數量不限，體現在我在遞歸里傳入的starIndex的值是i，而不是i+1了。之前說過for循環管控每一層數的寬度；遞歸則管控數的深度。這樣更改后，就可以在取完一個數的情況后，繼續取這個數。實現如下圖所示的效果：

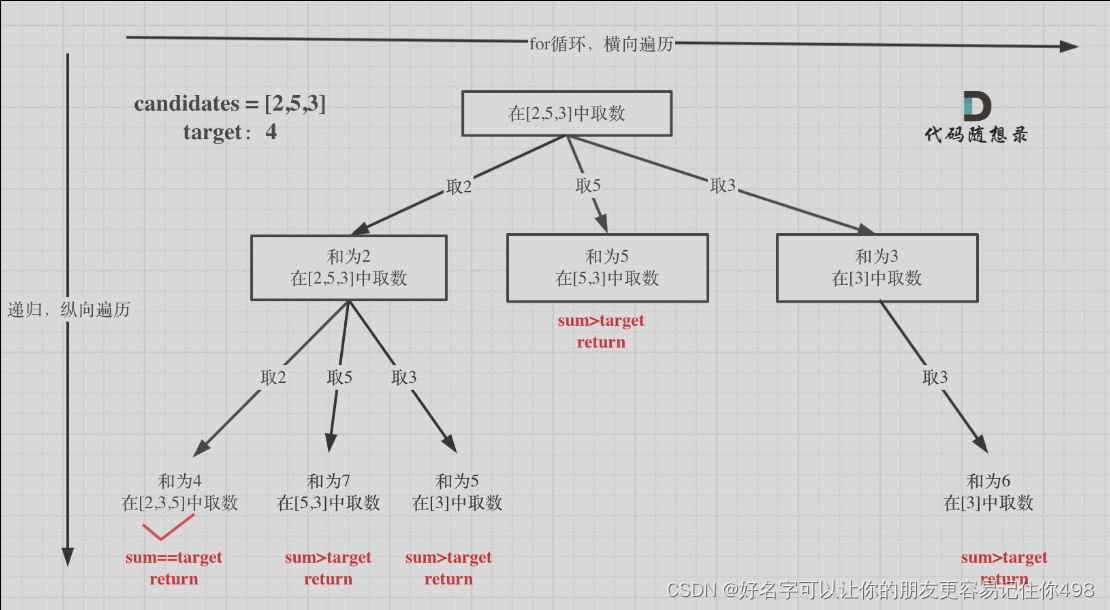
關于剪枝的操作。這種涉及到總和大小的取值時。剪枝就要將給定的數組排序！ 而且要注意給定的數組元素里全是正數，只有正數才越加越大。

這道題，我直接用目標總和target取減去每一個結點的數值了，看最后是否被減為0了。

2.組合總和2?

?題目鏈接/文章講解：代碼隨想錄

視頻講解：回溯算法中的去重，樹層去重樹枝去重，你弄清楚了沒？| LeetCode:40.組合總和II_嗶哩嗶哩_bilibili

?代碼：去重且剪枝過的

class Solution {
private:vector<int> path;vector<vector<int>> result;void backtracking(vector<int>& candidates,int target,int startIndex,vector<bool>& used){if(target < 0){return;}if(target == 0){result.push_back(path);return;}for(int i = startIndex;i < candidates.size() && target - candidates[i] >= 0;i++){// used[i - 1] == true，說明同一樹枝candidates[i - 1]使用過// used[i - 1] == false，說明同一樹層candidates[i - 1]使用過// 要對同一樹層使用過的元素進行跳過if(i > 0 && candidates[i] == candidates[i - 1] && used[i - 1] == false){continue;} // 數層去重used[i] = true;target -= candidates[i];path.push_back(candidates[i]);backtracking(candidates,target,i + 1,used);path.pop_back();target += candidates[i];used[i] = false;}}
public:vector<vector<int>> combinationSum2(vector<int>& candidates, int target) {vector<bool> used(candidates.size(),false);sort(candidates.begin(),candidates.end());backtracking(candidates,target,0,used);return result;}
};

思路:

這道題和上題的區別是：

每個元素只能使用一次——startIndex為i+1；

給定的元素有重復值，但是要去重后的結果：這里就是難點。首先去重是有兩個維度的。

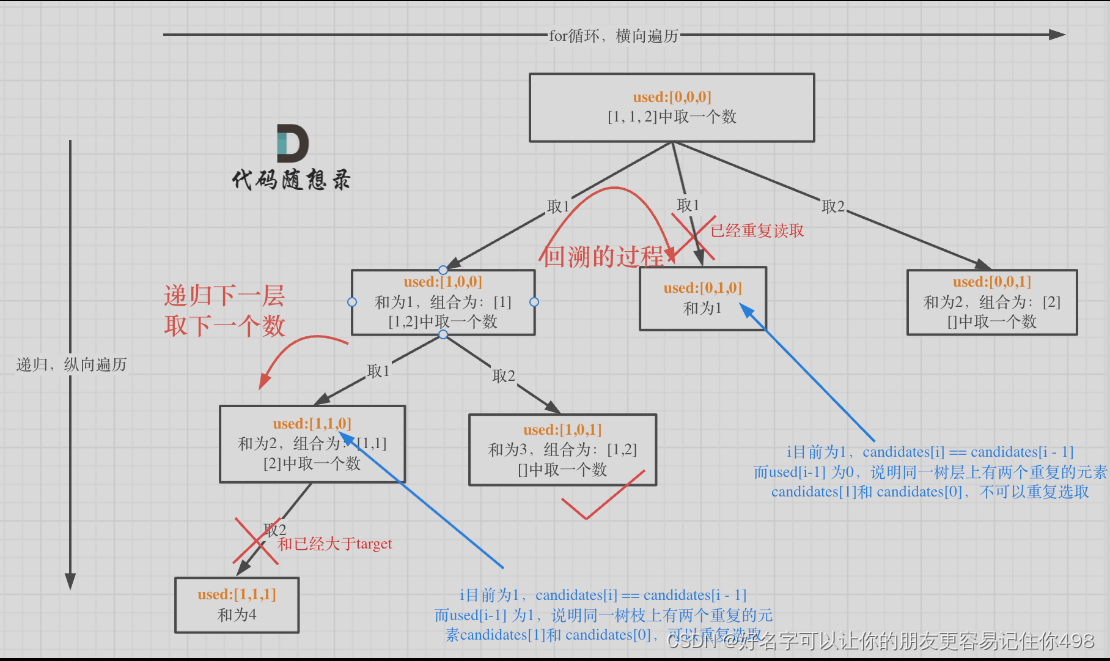
?一個組合里可以有相同大小的不同元素，所以遞歸操作里不需要去重，即上圖的同一個子樹的數枝上不需要去重；不同組合不能相同，所以要在數層去重。

這里用一個數組used來記錄，遇到的和前一個元素相同的情況（這里去重先去把給定數組排序）時，到底是和前一個相同元素是在同一個樹枝里的，還是同一個樹層里的。

在同一個樹枝里：前一個元素已經加入到了path里，已經使用過了。

在同一個樹層里：前一個元素沒有加入到path里，沒有被使用，這是獨立的兩個分支。

所以如果遇到這種樹層里重復的情況，加個判斷語句，直接continue（因為接下來的情況還有我們要收集的，所以只是跳過這一種情況，用continue）

3.分割回文串

代碼隨想錄

視頻講解：帶你學透回溯算法-分割回文串（對應力扣題目：131.分割回文串）| 回溯法精講！_嗶哩嗶哩_bilibili

?代碼：

class Solution {
private:vector<string> path;vector<vector<string>> result;bool isPalindrome(string& s,int start,int end){while(start <= end){if(s[start] != s[end]){return false;}start++;end--;}return true;}void backtracking(string& s,int startIndex){// 遞歸出口if(startIndex >= s.size()){result.push_back(path);return;}// 遍歷結點// 回文子串的范圍是[startIndex,i]for(int i = startIndex;i < s.size();i++){// 在這里直接判斷是否子串滿足回文子串if(isPalindrome(s,startIndex,i)){string str = s.substr(startIndex,i - startIndex + 1);path.push_back(str);}else{continue;}backtracking(s,i + 1);path.pop_back();}}
public:vector<vector<string>> partition(string s) {if(s.size() == 0) return result;backtracking(s,0);return result;}
};

思路：

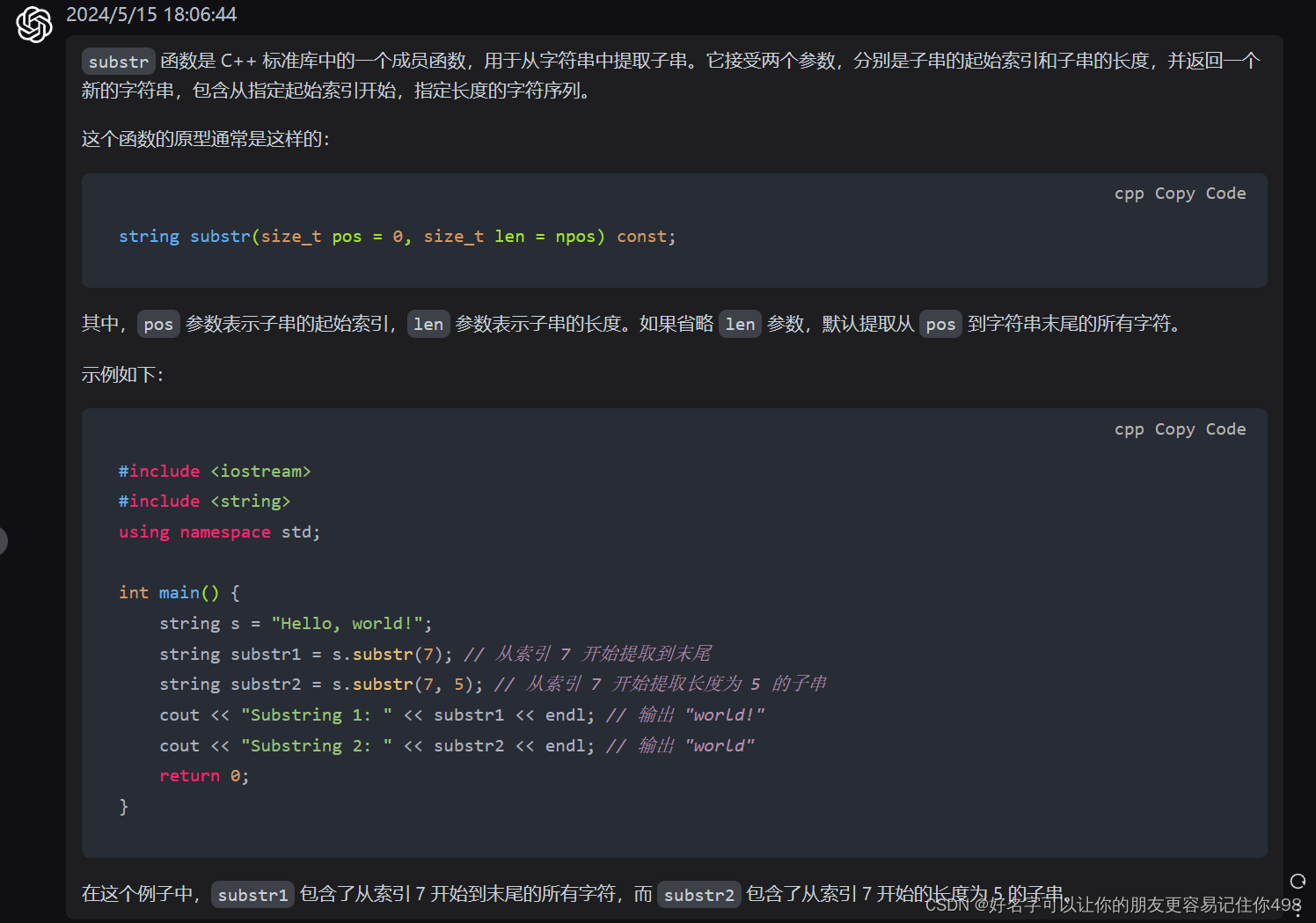
關于substr函數：

這道題很巧妙地將startIndex作為了子串的開始下標，子串的范圍可以表示為[startIndex,i]。

同時，本題將判斷條件放在了for循環的里面來判斷，來決定是否要執行下面的遞歸回溯操作。判斷用了一個額外的函數來判斷回文子串。?

細節問題其實就這些。