目錄
2.fpei文件下
2.6?number_solver.py
2.7 process.py
?2.8 taichi_solver.py
3. 算法總結
4. 代碼運行
4.1 測試
4.2?基于GUI后端自定義框輸出編輯圖像結果
4.2.1?下載open-cv
4.2.2?輸入命令
4.2.3?自定義框
4.2.4?按ESC退出
?
接續Fast-Poisson-Image-Editing代碼介紹(一)
2.fpei文件下
該包中的代碼與解析如下:
2.6?number_solver.py
????????提供了通過 Numba 加速的 Jacobi 方法的方程求解器和網格求解器的實現。這些實現包含了用于初始化、重置狀態、同步狀態、執行迭代步驟等方法。使用 Numba 的 njit?裝飾器加速部分計算密集型的迭代函數,提高求解器的性能。
from typing import Tuple # 導入了 Tuple類型,用于指示函數或變量應該是元組類型import numpy as np # # 導入了 numpy模塊,并為它分配一個別名 np.NumPy是Python中用于數值計算的強大庫。提供了對大型多維數組和矩陣的支持,以及對這些數組進行操作的數學函數集合
from numba import njit # 從numba模塊中導入了njit Numba是一個用于Python的實時(JIT)編譯器,它在運行時將Python函數翻譯成機器碼,這可以顯著提高數值計算的執行速度# equ_iter函數是一個被njit裝飾的函數,用于執行方程求解器的迭代步驟。
# 它接受矩陣的大小 N、矩陣 A、矩陣 B 和解向量 X 作為參數,并返回更新后的解向量
@njit(fastmath=True)
def equ_iter(N: int, A: np.ndarray, B: np.ndarray, X: np.ndarray) -> np.ndarray:return (B + X[A[:, 0]] + X[A[:, 1]] + X[A[:, 2]] + X[A[:, 3]]) / 4.0# grid_iter 函數是一個被njit裝飾的函數,用于執行網格求解器的迭代步驟。
# 它接受梯度圖像和目標圖像作為參數,并返回更新后的目標圖像
@njit(fastmath=True)
def grid_iter(grad: np.ndarray, tgt: np.ndarray) -> np.ndarray: # 定義了 grid_iter功能的。它有兩個參數: grad和 tgt,這兩個都是NumPy數組。函數的返回類型也是一個NumPy數組result = grad.copy() # 創建了一個 grad數組,并將其賦給變量 result.這樣就保證了原來的 grad在計算期間不會修改數組result[1:] += tgt[:-1] # 添加了 tgt數組向上偏移一個像素到 result數組中result[:-1] += tgt[1:] # 添加了 tgt數組向下偏移一個像素到 result數組中result[:, 1:] += tgt[:, :-1] # 添加了 tgt數組向左偏移一個像素 result數組中result[:, :-1] += tgt[:, 1:] # 添加了 tgt數組向右偏移一個像素 result數組中return result # 返回結果數組 resultclass EquSolver(object):"""Numba-based Jacobi method equation solver implementation."""def __init__(self) -> None:super().__init__() # 調用父類的構造函數self.N = 0 # 將實例對象N賦值為0# 該方法接受一個 np.ndarray 類型的參數 mask,表示掩碼圖像
# 函數返回一個 np.ndarray 類型的對象,表示生成的分區圖像def partition(self, mask: np.ndarray) -> np.ndarray:return np.cumsum((mask > 0).reshape(-1)).reshape(mask.shape)
# 該方法用于重置求解器的狀態,并接受四個參數:N(表示矩陣大小)、A(矩陣 A)、X(解向量 X)和 B(矩陣 B)def reset(self, N: int, A: np.ndarray, X: np.ndarray, B: np.ndarray) -> None:"""(4 - A)X = B"""self.N = N # 指定參數的值 N到實例變量 N對象self.A = A # 指定參數的值 A到實例變量 A對象self.B = B # 指定參數的值 B到實例變量 B對象self.X = equ_iter(N, A, B, X) # 指定調用 equ_iter函數的參數 N, A, B, 和 X到實例變量 X對象def sync(self) -> None:pass # 一個占位符方法,可以在以后實現同步
# 該方法用于執行求解器的迭代步驟,并接受一個整數類型的參數 iteration,表示要執行的迭代次數。
# 函數返回一個元組,包含兩個 np.ndarray 類型的對象,分別表示更新后的解向量和誤差def step(self, iteration: int) -> Tuple[np.ndarray, np.ndarray]:for _ in range(iteration):# X = (B + AX) / 4self.X = equ_iter(self.N, self.A, self.B, self.X)tmp = self.B + self.X[self.A[:, 0]] + self.X[self.A[:, 1]] + \self.X[self.A[:, 2]] + self.X[self.A[:, 3]] - 4.0 * self.Xerr = np.abs(tmp).sum(axis=0) # 計算錯誤的方法,取 tmp數組,沿指定的軸(軸= 0 )對它們求和,并將結果賦給 err變量的x = self.X.copy() # 創建了一個 self.X數組,并將其賦給變量 x.這樣就保證了原來的 self.X在計算期間不會修改數組x[x < 0] = 0 # 設置了所有的 x小于0數組為0,它約束解向量的值 x為非陰性x[x > 255] = 255 # 將x約束在0到255的范圍內return x, err # 返回約束后的解向量x和誤差err的元組# 該方法用于重置求解器的狀態,并接受四個參數:
# N(表示網格大小)、mask(掩碼圖像)、tgt(目標圖像)和grad(梯度圖像)
class GridSolver(object):"""Numba-based Jacobi method grid solver implementation."""def __init__(self) -> None:super().__init__() # 調用父類的構造函數self.N = 0 # 將實例對象N賦值為0def reset(self, N: int, mask: np.ndarray, tgt: np.ndarray, grad: np.ndarray) -> None: # 此方法用于重置對象的狀態。它需要四個參數: N(整數), mask, tgt, 和 grad(這三個都是NumPy數組)。這個方法的返回類型是 Noneself.N = N # 指定參數的值 N到實例變量 N對象self.mask = mask # 定參數的值 mask到實例變量 mask對象self.bool_mask = mask.astype(bool) # 使用 astype(bool)方法,將 mask數組轉換為布爾類型tmp = grid_iter(grad, tgt) # 通過調用grid_iter函數,將梯度圖像grad和目標圖像tgt作為參數來計算臨時變量tmptgt[self.bool_mask] = tmp[self.bool_mask] / 4.0self.tgt = tgt # 指定更新的目標圖像( tgt)轉換為實例變量 tgt對象self.grad = grad # 指定參數的值 grad到實例變量 grad對象def sync(self) -> None: # 方法為空pass # 是一個占位符方法,可以在以后實現同步def step(self, iteration: int) -> Tuple[np.ndarray, np.ndarray]: # 定義了 step類的方法。它取一個整數參數 iteration表示要執行的迭代次數。該方法的返回類型是包含兩個NumPy數組的元組for _ in range(iteration): # 開始一個循環,循環迭代 iteration次數tgt = grid_iter(self.grad, self.tgt) # 調用 grid_iter函數,并傳入 self.grad和 self.tgt作為參數,得到一個新的數組 tgtself.tgt[self.bool_mask] = tgt[self.bool_mask] / 4.0 # 將 tgt中對應掩碼為真的位置的值除以 4.0,并將結果賦值給 self.tgt中對應掩碼為真的位置# 在循環結束后,計算誤差tmp = 4 * self.tgt - self.grad # 創建一個臨時數組 tmp,計算公式為 4 * self.tgt - self.gradtmp[1:] -= self.tgt[:-1] # 將 self.tgt 在垂直方向上向下平移一行,并將結果與 tmp 對應位置相減tmp[:-1] -= self.tgt[1:] # 將 self.tgt在垂直方向上向上平移一行,并將結果與 tmp對應位置相減tmp[:, 1:] -= self.tgt[:, :-1] # 將 self.tgt在水平方向上向右平移一列,并將結果與 tmp對應位置相減tmp[:, :-1] -= self.tgt[:, 1:] # 將 self.tgt在水平方向上向左平移一列,并將結果與 tmp對應位置相減# 計算誤差errerr = np.abs(tmp[self.bool_mask]).sum(axis=0) # 通過對更新后的目標圖像self.tgt中對應掩碼為真的位置的值進行絕對值求和tgt = self.tgt.copy() # 創建一個副本tgt,將目標圖像self.tgt復制給它tgt[tgt < 0] = 0tgt[tgt > 255] = 255 # 將tgt約束在0到255的范圍內return tgt, err # 返回約束后的目標圖像tgt和誤差err的元組2.7 process.py
????????建立了一個圖像修復處理器的框架,具有不同的后端,允許用戶根據系統能力和偏好進行選擇。它包括解決 PIE 方程和執行基于網格的算法的功能,處理依賴關系,并提供錯誤消息,以實現無縫的用戶體驗。
import os # 導入了 Python 的 os模塊,用于與操作系統進行交互
from abc import ABC, abstractmethod # 從 abc模塊中導入了 ABC和 abstractmethod,用于定義抽象基類和抽象方法
from typing import Any, Optional, Tuple # 從 typing模塊中導入了 Any、 Optional和 Tuple,用于類型提示import numpy as np # 導入了 numpy庫,并將其命名為 np,用于進行數值計算和數組操作from fpie import np_solver # 入了一個名為 np_solver的模塊,用于提供一些與數值求解相關的功能或算法CPU_COUNT = os.cpu_count() or 1 # 用于獲取當前系統的CPU核心數量,如果無法獲取到CPU核心數量,則將其設為 1
DEFAULT_BACKEND = "numpy" # 示默認的后端選擇
ALL_BACKEND = ["numpy"] # 是一個列表,包含了所有可用的后端名稱try:from fpie import numba_solver # 嘗試導入numba_solver模塊,并將其添加到ALL_BACKEND列表中ALL_BACKEND += ["numba"] # 將字符串 "numba"添加到名為 ALL_BACKEND的列表變量中DEFAULT_BACKEND = "numba" # 將字符串 "numba"賦值給名為 DEFAULT_BACKEND的變量
except ImportError: # 如果導入失敗numba_solver = None # type: ignore # 則說明用戶安裝Numbatry:from fpie import taichi_solver # 嘗試導入 taichi_solver 模塊ALL_BACKEND += ["taichi-cpu", "taichi-gpu"] # 將字符串列表 ["taichi-cpu", "taichi-gpu"]添加到名為 ALL_BACKEND的列表變量中DEFAULT_BACKEND = "taichi-cpu" # 將字符串 "taichi-cpu"賦值給名為 DEFAULT_BACKEND的變量
except ImportError: # 如果導入失敗taichi_solver = None # type: ignore # 表示沒有可用的Taichi后端try:from fpie import core_gcc # 嘗試導入core_gcc模塊DEFAULT_BACKEND = "gcc" # 字符串 "gcc"賦值給名為 DEFAULT_BACKEND的變量ALL_BACKEND.append("gcc") # 將字符串 "gcc"添加到名為 ALL_BACKEND的列表變量中
except ImportError: # 如果導入失敗core_gcc = None # 則說明用戶安裝core_gcctry:from fpie import core_openmp # type: # ignore 嘗試導入core_openmp模塊DEFAULT_BACKEND = "openmp" # 將字符串 "openmp"賦值給名為 DEFAULT_BACKEND的變量ALL_BACKEND.append("openmp") # 將字符串 "openmp"添加到名為 ALL_BACKEND的列表變量中
except ImportError: # 如果導入失敗core_openmp = None # 則說明用戶安裝core_openmptry:from mpi4py import MPI # :嘗試從 mpi4py模塊中導入 MPIfrom fpie import core_mpi # type: ignoreALL_BACKEND.append("mpi") # 將字符串 "mpi"添加到名為 ALL_BACKEND的列表變量中
except ImportError: # 如果導入失敗MPI = None # type: ignorecore_mpi = None # 則說明用戶安裝core_mpitry:from fpie import core_cuda # 從 fpie模塊中導入 core_cudaDEFAULT_BACKEND = "cuda" # 將字符串 "cuda"賦值給名為 DEFAULT_BACKEND的變量ALL_BACKEND.append("cuda") # 將字符串 "cuda"添加到名為 ALL_BACKEND的列表變量中
except ImportError: # 如果導入失敗core_cuda = None # 則說明用戶安裝core_cudaclass BaseProcessor(ABC): # 定義了一個抽象基類BaseProcessor,用于處理圖像修復算法中的處理器"""API definition for processor class."""def __init__(self, gradient: str, rank: int, backend: str, core: Optional[Any]): # 方法接受四個參數: gradient、 rank、 backend和 core。其中, gradient是一個字符串, rank是一個整數, backend是一個字符串, core是一個可選的任意類型if core is None: # 如果 core為 None,即沒有提供有效的核心模塊,則執行以下操作error_msg = { # 創建一個字典 error_msg,其中包含不同后端的錯誤消息"numpy":"Please run `pip install numpy`.","numba":"Please run `pip install numba`.","gcc":"Please install cmake and gcc in your operating system.","openmp":"Please make sure your gcc is compatible with `-fopenmp` option.","mpi":"Please install MPI and run `pip install mpi4py`.","cuda":"Please make sure nvcc and cuda-related libraries are available.","taichi":"Please run `pip install taichi`.",}print(error_msg[backend.split("-")[0]]) # 打印對應后端的錯誤消息,根據 backend字符串中的第一個部分來選擇錯誤消息raise AssertionError(f"Invalid backend {backend}.") # 拋出一個斷言錯誤( AssertionError),并附帶錯誤消息,表示后端無效self.gradient = gradient # 表示梯度類型的字符串,可以是"src"、"avg"或其他self.rank = rank # 表示處理器的排名或標識符的整數self.backend = backend # 表示所使用的后端的字符串self.core = core # 表示具體的核心處理對象,可以是任意類型的對象self.root = rank == 0 # 表示是否為根節點的布爾值,根據 rank 的值進行判斷# 該方法用于混合兩個梯度向量,并返回混合后的結果。
# 它接受兩個 np.ndarray 類型的參數 a 和 b,表示要混合的兩個梯度向量def mixgrad(self, a: np.ndarray, b: np.ndarray) -> np.ndarray: # 定義了一個名為 mixgrad的方法,用于混合梯度的計算,該方法接受兩個參數 a和 b,都是 NumPy 數組類型。方法的返回類型也是一個 NumPy 數組if self.gradient == "src": # 值是"src",return a # 則直接返回參數aif self.gradient == "avg": # 值是"avg",return (a + b) / 2 # 則將參數a和b相加后除以2# mix gradient, see Equ. 12 in PIE papermask = np.abs(a) < np.abs(b) # 比較絕對值a[mask] = b[mask] # # 選擇性地 b中的元素替換到a中,以獲得更大的梯度值return a # 返回更新后的數組 a@abstractmethod # 使用了 @abstractmethod裝飾器,表示該方法是一個抽象方法,需要在子類中進行具體實現def reset( # 用于重置處理器的狀態self,src: np.ndarray, # 源圖像的np.ndarray數組mask: np.ndarray, # 掩碼圖像的np.ndarray數組tgt: np.ndarray, # 目標圖像的np.ndarray數組mask_on_src: Tuple[int, int], # 一個元組,表示掩碼在源圖像上的位置偏移mask_on_tgt: Tuple[int, int], # 一個元組,表示掩碼在目標圖像上的位置偏移) -> int: # 返回一個整數值,表示最大 ID 值passdef sync(self) -> None: # 該方法沒有參數,返回類型為 Noneself.core.sync() # 用于同步核心模塊的操作@abstractmethod # 使用了 @abstractmethod裝飾器,表示該方法是一個抽象方法,需要在子類中進行具體實現def step(self, iteration: int) -> Optional[Tuple[np.ndarray, np.ndarray]]:pass # 接受一個整數參數 iteration,返回類型為可選的元組,包含兩個 NumPy 數組class EquProcessor(BaseProcessor): # 定義了一個名為 EquProcessor的類,它是 BaseProcessor類的子類"""PIE Jacobi equation processor.""" # 該類用于處理 PIE Jacobi 方程def __init__(self,gradient: str = "max", # 表示梯度類型的字符串,默認為 "max"backend: str = DEFAULT_BACKEND, # 表示所使用的后端的字符串,默認為DEFAULT_BACKENDn_cpu: int = CPU_COUNT, # 表示使用的CPU核心數量,默認為CPU_COUNTmin_interval: int = 100, # 表示MPI最小間隔的整數,默認為100block_size: int = 1024, # 表示CUDA中的塊大小的整數,默認為1024):core: Optional[Any] = Nonerank = 0
# 以下if語句用于根據所選的后端選擇適當的核心處理對象,
# 并將其作為參數傳遞給父類BaseProcessor的初始化方法if backend == "numpy": # 如果后端為 "numpy"core = np_solver.EquSolver() # 則創建一個 np_solver.EquSolver 的實例并賦值給core變量。elif backend == "numba" and numba_solver is not None: # 如果后端為"numba"且 numba_solver 不為空core = numba_solver.EquSolver() # 則創建一個 numba_solver.EquSolver的實例elif backend == "gcc": # 如果 backend是 "gcc",core = core_gcc.EquSolver() # 則創建一個 core_gcc.EquSolver的實例elif backend == "openmp" and core_openmp is not None: # 如果 backend是 "openmp"并且 core_openmp不為空core = core_openmp.EquSolver(n_cpu) # 則創建一個帶有 n_cpu參數的 core_openmp.EquSolver的實例elif backend == "mpi" and core_mpi is not None: # 如果 backend是 "mpi"并且 core_mpi不為空core = core_mpi.EquSolver(min_interval) # 則創建一個帶有 min_interval參數的 core_mpi.EquSolver的實例,rank = MPI.COMM_WORLD.Get_rank() # 并獲取當前進程的 rankelif backend == "cuda" and core_cuda is not None: # 如果 backend是 "cuda"并且 core_cuda不為空core = core_cuda.EquSolver(block_size) # 則創建一個帶有 block_size參數的 core_cuda.EquSolver的實例elif backend.startswith("taichi") and taichi_solver is not None: # 如果 backend以 "taichi"開頭并且 taichi_solver不為空core = taichi_solver.EquSolver(backend, n_cpu, block_size) # 則創建一個帶有 backend、 n_cpu和 block_size參數的 taichi_solver.EquSolver的實例super().__init__(gradient, rank, backend, core) # 調用父類 BaseProcessor 的初始化方法,并傳遞梯度類型、排名、后端和核心處理對象作為參數進行初始化def mask2index( # 調用這個方法,可以將掩碼圖像轉換為相應的索引值,以便在圖像修復算法中使用self, mask: np.ndarray # 表示輸入的掩碼圖像) -> Tuple[np.ndarray, int, np.ndarray, np.ndarray]:x, y = np.nonzero(mask) # 通過 np.nonzero(mask)獲取掩碼圖像中非零元素的行坐標和列坐標,并分別賦值給 x和 ymax_id = x.shape[0] + 1 # 表示索引的最大值加1index = np.zeros((max_id, 3)) # 用于存儲索引信息ids = self.core.partition(mask) # 調用核心處理對象的partition方法,將掩碼圖像傳遞給它,并獲得分區后的結果idsids[mask == 0] = 0 # reserve id=0 for constantindex = ids[x, y].argsort() # 使用 ids[x, y]獲取掩碼圖像中非零位置對應的索引值,通過 argsort()方法進行排序,排序后的結果賦值給變量 indexreturn ids, max_id, x[index], y[index] # 將 ids、 max_id、根據索引排序后的非零行坐標 x[index]和列坐標 y[index]組成一個元組,并作為方法的返回值
#def reset( # 用于重置處理器的狀態self,src: np.ndarray, # 表示源圖像mask: np.ndarray, # 表示掩碼圖像tgt: np.ndarray, # 表示目標圖像mask_on_src: Tuple[int, int], # 表示掩碼在源圖像上的位置,是一個包含兩個整數的元組mask_on_tgt: Tuple[int, int], # 表示掩碼在目標圖像上的位置,是一個包含兩個整數的元組) -> int: # 返回類型是整數assert self.root # 進行斷言檢查。如果 self.root的值為真,則繼續執行;否則,會拋出 AssertionError異常# check validity# assert 0 <= mask_on_src[0] and 0 <= mask_on_src[1]# assert mask_on_src[0] + mask.shape[0] <= src.shape[0]# assert mask_on_src[1] + mask.shape[1] <= src.shape[1]# assert mask_on_tgt[0] + mask.shape[0] <= tgt.shape[0]# assert mask_on_tgt[1] + mask.shape[1] <= tgt.shape[1]if len(mask.shape) == 3: # 如果掩碼圖像的維度為 3,mask = mask.mean(-1) # 則取各通道的均值,將其轉換為二維圖像mask = (mask >= 128).astype(np.int32) # 將掩碼圖像中大于等于 128 的像素值設為 1
# 對邊緣進行零填充操作,將掩碼圖像的四個邊界位置都設置為0# zero-out edgemask[0] = 0 # 將第一行的像素值設為 0mask[-1] = 0 # 將最后一行的像素值設為 0mask[:, 0] = 0 # 將第一列的像素值設為 0mask[:, -1] = 0 # 將最后一列的像素值設為 0x, y = np.nonzero(mask) # 獲取掩碼圖像中非零元素的行坐標和列坐標,并分別賦值給 x和 yx0, x1 = x.min() - 1, x.max() + 2 # 分別獲取行坐標的最小值和最大值,并進行調整得到新的范圍 x0和 x1y0, y1 = y.min() - 1, y.max() + 2 # 分別獲取列坐標的最小值和最大值,并進行調整得到新的范圍 y0和 y1mask_on_src = (x0 + mask_on_src[0], y0 + mask_on_src[1]) # 計算調整后的偏移mask_on_tgt = (x0 + mask_on_tgt[0], y0 + mask_on_tgt[1]) # 計算調整后的偏移mask = mask[x0:x1, y0:y1] # 根據調整后的索引范圍 x0、 x1、 y0和 y1,從原始的掩碼圖像中提取相應區域的子圖像,并將其賦值給變量 maskids, max_id, index_x, index_y = self.mask2index(mask) # 將調整后的掩碼圖像 mask作為參數傳遞給該方法,并獲取返回的結果src_x, src_y = index_x + mask_on_src[0], index_y + mask_on_src[1] # 將 index_x加上 mask_on_src[0]得到源圖像中的行坐標 src_x,將 index_y加上 mask_on_src[1]得到源圖像中的列坐標 src_ytgt_x, tgt_y = index_x + mask_on_tgt[0], index_y + mask_on_tgt[1] # 將 index_x加上 mask_on_tgt[0]得到目標圖像中的行坐標 tgt_x,將 index_y加上 mask_on_tgt[1]得到目標圖像中的列坐標 tgt_y
# 根據調整后的索引和偏移,從源圖像和目標圖像中提取相應位置上的像素值,分別存儲在以下變量中src_C = src[src_x, src_y].astype(np.float32) # 通過索引操作 src[src_x, src_y],將源圖像中 src_x和 src_y坐標位置上的像素值賦值給變量 src_Csrc_U = src[src_x - 1, src_y].astype(np.float32) # 從源圖像中提取了 src_x - 1行、 src_y列位置上的像素值,并將其轉換為 np.float32類型,賦值給變量 src_Usrc_D = src[src_x + 1, src_y].astype(np.float32) # 從源圖像中提取了 src_x + 1行、 src_y列位置上的像素值,并將其轉換為 np.float32類型,賦值給變量 src_Dsrc_L = src[src_x, src_y - 1].astype(np.float32) # 從源圖像中提取了 src_x行、 src_y - 1列位置上的像素值,并將其轉換為 np.float32類型,賦值給變量 src_Lsrc_R = src[src_x, src_y + 1].astype(np.float32) # 從源圖像中提取了 src_x行、 src_y + 1列位置上的像素值,并將其轉換為 np.float32類型,賦值給變量 src_Rtgt_C = tgt[tgt_x, tgt_y].astype(np.float32) # 從目標圖像中提取了 tgt_x行、 tgt_y列位置上的像素值,并將其轉換為 np.float32類型,賦值給變量 tgt_Ctgt_U = tgt[tgt_x - 1, tgt_y].astype(np.float32) # 從目標圖像中提取了 tgt_x - 1行、 tgt_y列位置上的像素值,并將其轉換為 np.float32類型,賦值給變量 tgt_Utgt_D = tgt[tgt_x + 1, tgt_y].astype(np.float32) # 從目標圖像中提取了 tgt_x + 1行、 tgt_y列位置上的像素值,并將其轉換為 np.float32類型,賦值給變量 tgt_Dtgt_L = tgt[tgt_x, tgt_y - 1].astype(np.float32) # 從 tgt指定的原始位置左偏移一個單位的位置上的數組 (tgt_x, tgt_y)。然后將這些值強制轉換為 np.float32并存儲在變量中 tgt_Ltgt_R = tgt[tgt_x, tgt_y + 1].astype(np.float32) # 從 tgt指定的原始位置右偏移一個單位的位置上的數組 (tgt_x, tgt_y)。然后將這些值強制轉換為 np.float32并存儲在變量中 tgt_R
# 根據源圖像和目標圖像的像素值計算梯度 grad,使用 self.mixgrad 方法混合不同梯度類型的值grad = self.mixgrad(src_C - src_L, tgt_C - tgt_L) \+ self.mixgrad(src_C - src_R, tgt_C - tgt_R) \+ self.mixgrad(src_C - src_U, tgt_C - tgt_U) \+ self.mixgrad(src_C - src_D, tgt_C - tgt_D)
# 創建了三個矩陣:A、X和B,用于存儲線性方程組的系數和常數項A = np.zeros((max_id, 4), np.int32) # 創建一個NumPy數組 A與尺寸 (max_id, 4)和數據類型 np.int32.數組用零初始化X = np.zeros((max_id, 3), np.float32) # 創建一個NumPy數組 X與尺寸 (max_id, 3)和數據類型 np.float32.數組用零初始化B = np.zeros((max_id, 3), np.float32) # 創建一個NumPy數組 B與尺寸 (max_id, 3)和數據類型 np.float32.數組用零初始化
# 目標圖像中對應位置的像素值賦值給 X 矩陣中的一部分X[1:] = tgt[index_x + mask_on_tgt[0], index_y + mask_on_tgt[1]]# four-wayA[1:, 0] = ids[index_x - 1, index_y] # 將 ids[index_x - 1, index_y]的值賦給 A數組第一列(除去第一行)A[1:, 1] = ids[index_x + 1, index_y] # ids[index_x + 1, index_y]的值賦給 A數組第二列(除去第一行)A[1:, 2] = ids[index_x, index_y - 1] # 將 ids[index_x, index_y - 1]的值賦給 A數組第三列(除去第一行)A[1:, 3] = ids[index_x, index_y + 1] # 將 ids[index_x, index_y + 1]的值賦給 A數組第四列(除去第一行)B[1:] = grad # 將 grad數組的值賦給 B數組的第二行及之后的所有行m = (mask[index_x - 1, index_y] == 0).astype(float).reshape(-1, 1) # 根據 mask數組中指定索引位置的值是否為0,生成一個布爾型數組,并將其轉換為浮點型數組,然后將其形狀調整為列向量B[1:] += m * tgt[index_x + mask_on_tgt[0] - 1, index_y + mask_on_tgt[1]] # 將 tgt數組中指定索引位置的值與上述生成的布爾型數組相乘,并將結果加到 B數組的第二行及之后的所有行上m = (mask[index_x, index_y - 1] == 0).astype(float).reshape(-1, 1) # 生成一個布爾型數組,并將其轉換為浮點型數組,然后將其形狀調整為列向量B[1:] += m * tgt[index_x + mask_on_tgt[0], index_y + mask_on_tgt[1] - 1] # 將 tgt數組中指定索引位置的值與上述生成的布爾型數組相乘,并將結果加到 B數組的第二行及之后的所有行上m = (mask[index_x, index_y + 1] == 0).astype(float).reshape(-1, 1) # 生成一個布爾型數組,并將其轉換為浮點型數組,然后將其形狀調整為列向量B[1:] += m * tgt[index_x + mask_on_tgt[0], index_y + mask_on_tgt[1] + 1] # 將 tgt數組中指定索引位置的值與上述生成的布爾型數組相乘,并將結果加到 B數組的第二行及之后的所有行上m = (mask[index_x + 1, index_y] == 0).astype(float).reshape(-1, 1) # 根據mask數組中指定索引位置的值是否為0,生成一個布爾型數組,并將其轉換為浮點型數組,然后將其形狀調整為列向量B[1:] += m * tgt[index_x + mask_on_tgt[0] + 1, index_y + mask_on_tgt[1]] # 將tgt數組中指定索引位置的值與上述生成的布爾型數組相乘,并將結果加到B數組的第二行及之后的所有行上self.tgt = tgt.copy() # 將變量tgt進行深拷貝,賦值給self.tgt,避免對原始數據的修改self.tgt_index = (index_x + mask_on_tgt[0], index_y + mask_on_tgt[1]) # 計算出一個元組,并將其賦值給self.tgt_index。這個元組表示了目標索引的位置self.core.reset(max_id, A, X, B) # 調用self.core對象的reset方法,并傳遞參數max_id、A、X和Breturn max_id # 返回變量max_id
# 該方法用于執行迭代步驟def step(self, iteration: int) -> Optional[Tuple[np.ndarray, np.ndarray]]:result = self.core.step(iteration) # 將計算結果中的修復后的像素值x更新到目標圖像中的相應位置if self.root: # 如果當前處理器是根節點x, err = result # 回修復后的圖像和誤差self.tgt[self.tgt_index] = x[1:] # 將x中從第二個元素開始的部分(即x[1:])賦值給self.tgt數組中的指定索引位置self.tgt_index。這樣做是將修復后的像素值更新到目標圖像中的相應位置return self.tgt, err # 返回self.tgt和err作為函數或方法的結果,以元組的形式返回return None # 如果當前處理器不是根節點,則返回None# 該類繼承自BaseProcessor類,用于執行PIE算法中的網格處理器
class GridProcessor(BaseProcessor):"""PIE grid processor."""def __init__(self,gradient: str = "max", # 表示梯度類型的字符串backend: str = DEFAULT_BACKEND, # 表示所使用的后端的字符串n_cpu: int = CPU_COUNT, # 表示使用的 CPU 核心數量min_interval: int = 100, # 表示MPI最小間隔的整數block_size: int = 1024, # 表示CUDA中的塊大小的整數grid_x: int = 8, # 表示網格在x軸上的數量的整數,默認為8grid_y: int = 8, # 表示網格在y軸上的數量的整數,默認為8):core: Optional[Any] = Nonerank = 0
# 根據后端的不同選擇具體的核心處理對象,并將其傳遞給基類 BaseProcessor 進行初始化if backend == "numpy": # 如果 backend 是 "numpy",core = np_solver.GridSolver() # 則創建一個 np_solver.GridSolver() 對象,并賦值給變量 coreelif backend == "numba" and numba_solver is not None: # 如果 backend 是 "numba" 并且 numba_solver 不為空core = numba_solver.GridSolver() # 創建一個 numba_solver.GridSolver() 對象,并賦值給變量 coreelif backend == "gcc": # 如果 backend 是 "gcc",core = core_gcc.GridSolver(grid_x, grid_y) # 則創建一個 core_gcc.GridSolver(grid_x, grid_y) 對象,并賦值給變量 coreelif backend == "openmp" and core_openmp is not None: # 如果 backend 是 "openmp" 并且 core_openmp 不為空core = core_openmp.GridSolver(grid_x, grid_y, n_cpu) # 則創建一個 core_openmp.GridSolver(grid_x, grid_y, n_cpu) 對象,并賦值給變量 coreelif backend == "mpi" and core_mpi is not None: # 如果 backend 是 "mpi" 并且 core_mpi 不為空core = core_mpi.GridSolver(min_interval) # 則創建一個 core_mpi.GridSolver(min_interval) 對象,并賦值給變量 corerank = MPI.COMM_WORLD.Get_rank() # 同時,獲取當前進程的排名并賦值給變量 rankelif backend == "cuda" and core_cuda is not None: # 如果 backend 是 "cuda" 并且 core_cuda 不為空core = core_cuda.GridSolver(grid_x, grid_y) # 則創建一個 core_cuda.GridSolver(grid_x, grid_y) 對象,并賦值給變量 coreelif backend.startswith("taichi") and taichi_solver is not None: # 如果 backend 以 "taichi" 開頭并且 taichi_solver 不為空core = taichi_solver.GridSolver( # 創建一個 taichi_solver.GridSolver(grid_x, grid_y, backend, n_cpu, block_size) 對象,并賦值給變量 coregrid_x, grid_y, backend, n_cpu, block_size)super().__init__(gradient, rank, backend, core) # 調用基類 BaseProcessor 的初始化方法,傳遞梯度、排名、后端和核心處理對象進行初始化def reset(self,src: np.ndarray, # 表示源圖像的numpy數組mask: np.ndarray, # 表示掩碼圖像的numpy數組tgt: np.ndarray, # 表示目標圖像的numpy數組mask_on_src: Tuple[int, int], # 表示在源圖像上的掩碼位置的元組mask_on_tgt: Tuple[int, int], # 表示在目標圖像上的掩碼位置的元組) -> int:assert self.root # 斷言當前處理器是根節點。如果不是根節點,則會引發異常# check validity# assert 0 <= mask_on_src[0] and 0 <= mask_on_src[1]# assert mask_on_src[0] + mask.shape[0] <= src.shape[0]# assert mask_on_src[1] + mask.shape[1] <= src.shape[1]# assert mask_on_tgt[0] + mask.shape[0] <= tgt.shape[0]# assert mask_on_tgt[1] + mask.shape[1] <= tgt.shape[1]if len(mask.shape) == 3: # 檢查掩碼圖像的維度是否為3,即是否為彩色圖像 如果是彩色圖像,則執行下一步操作mask = mask.mean(-1) # 對彩色圖像的最后一個維度進行求平均操作,將其轉換為灰度圖像。這樣做是為了將彩色圖像轉換為單通道的灰度圖像mask = (mask >= 128).astype(np.int32) # 將灰度圖像中大于等于128的像素值設置為1,小于128的像素值設置為0,并將結果轉換為np.int32類型
# 對邊緣進行零填充操作,將掩碼圖像的四個邊界位置都設置為 0# zero-out edgemask[0] = 0 # 將掩碼圖像的第一行(上邊界)的所有元素設置為0mask[-1] = 0 # 將掩碼圖像的最后一行(下邊界)的所有元素設置為0mask[:, 0] = 0 # 將掩碼圖像的第一列(左邊界)的所有元素設置為0mask[:, -1] = 0 # 將掩碼圖像的最后一列(右邊界)的所有元素設置為0x, y = np.nonzero(mask) # 找到掩碼圖像中非零元素的索引坐標,并將其分別保存在x和y中x0, x1 = x.min() - 1, x.max() + 2 # 計算變量 x 的最小值減去1,得到 x0;計算變量 x 的最大值加上2,得到 x1y0, y1 = y.min() - 1, y.max() + 2 # 計算變量 y 的最小值減去1,得到 y0;計算變量 y 的最大值加上2,得到 y1mask = mask[x0:x1, y0:y1] # 根據計算出的索引范圍,從原始的掩碼圖像中提取相應區域的子圖像,更新mask變量max_id = np.prod(mask.shape) # 得到最大 ID 值# 用于計算修復區域的梯度
# 從源圖像 src 和目標圖像 tgt 中根據掩碼位置偏移和索引范圍裁剪出相應區域的子圖像,并將它們轉換為 np.float32 類型src_crop = src[mask_on_src[0] + x0:mask_on_src[0] + x1,mask_on_src[1] + y0:mask_on_src[1] + y1].astype(np.float32)tgt_crop = tgt[mask_on_tgt[0] + x0:mask_on_tgt[0] + x1,mask_on_tgt[1] + y0:mask_on_tgt[1] + y1].astype(np.float32)grad = np.zeros([*mask.shape, 3], np.float32)grad[1:] += self.mixgrad( # 表示下方向的梯度src_crop[1:] - src_crop[:-1], tgt_crop[1:] - tgt_crop[:-1])grad[:-1] += self.mixgrad( # 表示上方向的梯度src_crop[:-1] - src_crop[1:], tgt_crop[:-1] - tgt_crop[1:])grad[:, 1:] += self.mixgrad( # 表示右方向的梯度src_crop[:, 1:] - src_crop[:, :-1], tgt_crop[:, 1:] - tgt_crop[:, :-1])grad[:, :-1] += self.mixgrad( # 表示左方向的梯度src_crop[:, :-1] - src_crop[:, 1:], tgt_crop[:, :-1] - tgt_crop[:, 1:])grad[mask == 0] = 0 # 將 grad 中掩碼為 0 的位置的梯度值設置為 0。# 這樣可以確保在修復過程中,只有在掩碼區域內的像素才會受到梯度的影響,而在掩碼區域外的像素則不受影響self.x0 = mask_on_tgt[0] + x0 # 將 mask_on_tgt[0] 和 x0 相加的結果賦值給 self.x0。這個操作是為了計算目標圖像中裁剪區域的左上角在整個圖像中的位置self.x1 = mask_on_tgt[0] + x1 # 將 mask_on_tgt[0] 和 x1 相加的結果賦值給 self.x1。這個操作是為了計算目標圖像中裁剪區域的右下角在整個圖像中的位置self.y0 = mask_on_tgt[1] + y0 # 將 mask_on_tgt[1] 和 y0 相加的結果賦值給 self.y0。這個操作是為了計算目標圖像中裁剪區域的左上角在整個圖像中的位置self.y1 = mask_on_tgt[1] + y1 # 將 mask_on_tgt[1] 和 y1 相加的結果賦值給 self.y1。這個操作是為了計算目標圖像中裁剪區域的右下角在整個圖像中的位置self.tgt = tgt.copy() # 將變量 tgt 進行深拷貝,賦值給 self.tgt。這樣做是為了避免對原始數據的修改self.core.reset(max_id, mask, tgt_crop, grad) # 用 self.core 對象的 reset 方法,并傳遞參數 max_id、mask、tgt_crop 和 grad。對 self.core 對象進行一些重置操作return max_id # 返回變量 max_iddef step(self, iteration: int) -> Optional[Tuple[np.ndarray, np.ndarray]]:result = self.core.step(iteration) # 調用 self.core 對象的 step 方法,并傳遞參數 iterationif self.root: # 如果當前處理器是根節點tgt, err = result # 將計算結果中的修復后的像素值tgt更新到目標圖像self.tgt中的相應位置self.tgt[self.x0:self.x1, self.y0:self.y1] = tgtreturn self.tgt, err # 返回修復后的圖像和誤差return None2.8 taichi_solver.py
????????實現基于 Taichi 的 Jacobi 方法,用于求解線性方程組和執行圖像修復任務。 Jacobi 方法被應用于網格上,通過迭代更新目標圖像的值,并計算誤差,以實現對圖像的修復。
from typing import Tuple # 從 typing 模塊中導入 Tuple 類型,用于定義元組類型的注解import numpy as np # 導入 numpy 庫,并將其命名為 np,用于進行科學計算和數組操作
import taichi as ti # 導入 taichi 庫,并將其命名為 ti,用于進行物理仿真和圖形計算@ti.data_oriented
class EquSolver(object):"""Taichi-based Jacobi method equation solver implementation."""# 初始化方法,接受后端類型、CPU核心數量和塊大小等參數def __init__(self, backend: str, n_cpu: int, block_size: int) -> None:super().__init__()self.parallelize = n_cpu # 并行化標志,表示使用的 CPU 核心數量self.block_dim = block_size # 塊大小,用于指定 Tiachi 并行計算的塊維度ti.init(arch=getattr(ti, backend.split("-")[-1])) # 初始化Taichi環境,指定所使用的后端類型和架構self.N = 0 # 線性方程組的大小,默認為 0self.fb: ti.FieldsBuilder # Taichi中用于構建字段的輔助對象self.fbst: ti._snode.snode_tree.SNodeTree # Taichi中用于構建字段的輔助對象
# Taichi 字段,分別用于存儲誤差、系數矩陣、常數項、未知變量和臨時變量self.terr = ti.field(ti.f32, (3,)) # 創建一個名為 terr 的 Taichi 字段,存儲誤差,數據類型為 ti.f32(單精度浮點數),形狀為 (3,)self.tA = ti.field(ti.i32) # 創建一個名為 tA 的 Taichi 字段,存儲系數矩陣,數據類型為 ti.i32(32位整數)self.tB = ti.field(ti.f32) # 創建一個名為 tB 的 Taichi 字段,存儲常數項,數據類型為 ti.f32self.tX = ti.field(ti.f32) # 創建一個名為 tX 的 Taichi 字段,存儲未知變量,數據類型為 ti.f32self.tmp = ti.field(ti.f32) # 創建一個名為 tmp 的 Taichi 字段,存儲臨時變量,數據類型為 ti.f32def partition(self, mask: np.ndarray) -> np.ndarray: # 這個方法接受一個名為 mask 的 numpy 數組作為參數,并返回一個 numpy 數組return np.cumsum((mask > 0).reshape(-1)).reshape(mask.shape)
# 調用這個方法,可以設置線性方程組的大小、系數矩陣、未知變量的初始值和常數項,并初始化Taichi字段def reset(self, N: int, A: np.ndarray, X: np.ndarray, B: np.ndarray) -> None:"""(4 - A)X = B"""self.N = N # 將參數 N 的值賦給實例變量 N,表示線性方程組的大小self.A = A # 將參數 A 的值賦給實例變量 A,表示系數矩陣self.B = B # 將參數 B 的值賦給實例變量 B,表示常數項self.X = X # 將參數 X 的值賦給實例變量 X,表示未知變量if hasattr(self, "fbst"): # 檢查是否已經存在Taichi字段構建器 fbstself.fbst.destroy() # 存在則銷毀它,并重新創建tAtB、tX和tmp字段self.tA = ti.field(ti.i32) # 重新創建 tA 字段,數據類型為 ti.i32self.tB = ti.field(ti.f32) # 重新創建 tB 字段,數據類型為 ti.f32self.tX = ti.field(ti.f32) # 重新創建 tX 字段,數據類型為 ti.f32self.tmp = ti.field(ti.f32) # 重新創建 tmp 字段,數據類型為 ti.f32self.fb = ti.FieldsBuilder() # 創建一個新的字段構建器對象self.fb.dense(ti.ij, (N, 4)).place(self.tA) # 使用字段構建器將 tA 字段放置在二維網格 (N, 4) 上self.fb.dense(ti.ij, (N, 3)).place(self.tB) # 使用字段構建器將 tB 字段放置在二維網格 (N, 3) 上self.fb.dense(ti.ij, (N, 3)).place(self.tX) # 使用字段構建器將 tX 字段放置在二維網格 (N, 3) 上self.fb.dense(ti.ij, (N, 3)).place(self.tmp) # 使用字段構建器將 tmp 字段放置在二維網格 (N, 3) 上self.fbst = self.fb.finalize() # 使用字段構建器的 finalize() 方法完成字段的創建和布局self.tA.from_numpy(A) # 參數 A 的值從 numpy 數組轉換為 Taichi 字段self.tB.from_numpy(B) # 將參數 B 的值從 numpy 數組轉換為 Taichi 字段self.tX.from_numpy(X) # 將參數 X 的值從 numpy 數組轉換為 Taichi 字段self.tmp.from_numpy(X) # 將參數 X 的值從 numpy 數組轉換為 Taichi 字段def sync(self) -> None: # 用于同步操作pass@ti.kernel # 定義了一個核函數 iter_kernel,用于執行 Jacobi 迭代方def iter_kernel(self) -> int: # 定義了 iter_kernel 方法,用于執行Jacobi迭代方法的核函數ti.loop_config(parallelize=self.parallelize, block_dim=self.block_dim) # 配置并行化和塊大小參數for i in range(1, self.N): # 對于 i 在范圍從 1 到 self.N 的循環迭代i0, i1 = self.tA[i, 0], self.tA[i, 1] # 將 self.tA[i, 0] 和 self.tA[i, 1] 的值分別賦給 i0 和 i1i2, i3 = self.tA[i, 2], self.tA[i, 3] # 將 self.tA[i, 2] 和 self.tA[i, 3] 的值分別賦給 i2 和 i3# X = (B + AX) / 4self.tX[i, 0] = (self.tB[i, 0] + self.tX[i0, 0] + self.tX[i1, 0] + self.tX[i2, 0] +self.tX[i3, 0]) / 4.0 # 根據 Jacobi 迭代方法的公式,計算 tX[i, 0] 的值,并將結果賦給它self.tX[i, 1] = (self.tB[i, 1] + self.tX[i0, 1] + self.tX[i1, 1] + self.tX[i2, 1] +self.tX[i3, 1]) / 4.0 # 根據 Jacobi 迭代方法的公式,計算 tX[i, 1] 的值,并將結果賦給它self.tX[i, 2] = (self.tB[i, 2] + self.tX[i0, 2] + self.tX[i1, 2] + self.tX[i2, 2] +self.tX[i3, 2]) / 4.0 # 根據 Jacobi 迭代方法的公式,計算 tX[i, 2] 的值,并將結果賦給它return 0@ti.kerneldef error_kernel(self) -> int: # 該方法用于計算誤差ti.loop_config(parallelize=self.parallelize, block_dim=self.block_dim) # 配置并行化和塊大小參數for i in range(1, self.N):i0, i1 = self.tA[i, 0], self.tA[i, 1]i2, i3 = self.tA[i, 2], self.tA[i, 3]self.tmp[i, 0] = ti.abs(self.tB[i, 0] + self.tX[i0, 0] + self.tX[i1, 0] + self.tX[i2, 0] +self.tX[i3, 0] - 4.0 * self.tX[i, 0])self.tmp[i, 1] = ti.abs(self.tB[i, 1] + self.tX[i0, 1] + self.tX[i1, 1] + self.tX[i2, 1] +self.tX[i3, 1] - 4.0 * self.tX[i, 1])self.tmp[i, 2] = ti.abs(self.tB[i, 2] + self.tX[i0, 2] + self.tX[i1, 2] + self.tX[i2, 2] +self.tX[i3, 2] - 4.0 * self.tX[i, 2])self.terr[0] = self.terr[1] = self.terr[2] = 0ti.loop_config(parallelize=self.parallelize, block_dim=self.block_dim)for i, j in self.tmp:self.terr[j] += self.tmp[i, j]return 0
# 用于執行迭代步驟def step(self, iteration: int) -> Tuple[np.ndarray, np.ndarray]:for _ in range(iteration): # 指定次數的迭代self.iter_kernel() # 更新未知變量的值self.error_kernel() # 計算最終的誤差x = self.tX.to_numpy()x[x < 0] = 0x[x > 255] = 255 # 保像素值范圍在 0 到 255 之間return x, self.terr.to_numpy()@ti.data_oriented
class GridSolver(object):"""Taichi-based Jacobi method grid solver implementation."""def __init__(self, grid_x: int, grid_y: int, backend: str, n_cpu: int, block_size: int) -> None:super().__init__()self.N = 0self.grid_x = grid_x # 網格在x軸的數量self.grid_y = grid_y # 網格在y軸的數量self.parallelize = n_cpu # CPU 核心數量,用于并行化計算self.block_dim = block_size # 塊大小,用于指定Taichi并行計算的塊維度ti.init(arch=getattr(ti, backend.split("-")[-1])) # 始化Taichi環境,指定所使用的后端類型和架構self.fb: ti.FieldsBuilderself.fbst: ti._snode.snode_tree.SNodeTreeself.terr = ti.field(ti.f32, (3,))self.tmask = ti.field(ti.i32)self.ttgt = ti.field(ti.f32)self.tgrad = ti.field(ti.f32)self.tmp = ti.field(ti.f32)
# 該方法用于重置GridSolver對象的狀態
# 在方法內部,首先根據網格的數量和掩碼的形狀計算出新的修復區域的大小,并保存原始的修復區域大小def reset( # reset方法的另一部分,用于重新創建和初始化Taichi字段self, N: int, mask: np.ndarray, tgt: np.ndarray, grad: np.ndarray) -> None:gx, gy = self.grid_x, self.grid_yself.orig_N, self.orig_M = N, M = mask.shape # 首先計算修復區域的大小,并將其保存為N和M的值pad_x = 0 if N % gx == 0 else gx - (N % gx)pad_y = 0 if M % gy == 0 else gy - (M % gy)if pad_x or pad_y: # 如果修復區域的大小不能被網格塊的大小整除mask = np.pad(mask, [(0, pad_x), (0, pad_y)]) # 則使用np.pad函數對數組進行填充tgt = np.pad(tgt, [(0, pad_x), (0, pad_y), (0, 0)])grad = np.pad(grad, [(0, pad_x), (0, pad_y), (0, 0)])self.N, self.M = N, M = mask.shapebx, by = N // gx, M // gyself.mask = maskself.tgt = tgtself.grad = gradif hasattr(self, "fbst"): # 首先檢查是否已經存在Taichi字段fbstself.fbst.destroy() # 如果存在,則調用destroy方法銷毀它self.tmask = ti.field(ti.i32) # 并重新創建以下字段self.ttgt = ti.field(ti.f32)self.tgrad = ti.field(ti.f32)self.tmp = ti.field(ti.f32)self.fb = ti.FieldsBuilder() # 使用Taichi字段構建器fb創建字段# 通過多次調用 dense 方法可以創建多級的嵌套字段self.fb.dense(ti.ij, (bx, by)).dense(ti.ij, (gx, gy)).place(self.tmask)self.fb.dense(ti.ij, (bx, by)).dense(ti.ij, (gx, gy)) \.dense(ti.k, 3).place(self.ttgt)self.fb.dense(ti.ij, (bx, by)).dense(ti.ij, (gx, gy)) \.dense(ti.k, 3).place(self.tgrad)self.fb.dense(ti.ij, (bx, by)).dense(ti.ij, (gx, gy)) \.dense(ti.k, 3).place(self.tmp)self.fbst = self.fb.finalize()self.tmask.from_numpy(mask)self.ttgt.from_numpy(tgt)self.tgrad.from_numpy(grad)self.tmp.from_numpy(grad)def sync(self) -> None:pass@ti.kerneldef iter_kernel(self) -> int: # 用于執行網格求解中的 Jacobi 迭代步驟ti.loop_config(parallelize=self.parallelize, block_dim=self.block_dim) # 配置并行化和塊大小參數for i, j in self.tmask: # 于每個索引 (i, j),根據Jacobi迭代公式計算出目標圖像ttgt在當前像素位置的更新值if self.tmask[i, j] > 0:# tgt = (grad + Atgt) / 4self.ttgt[i, j, 0] = (self.tgrad[i, j, 0] + self.ttgt[i - 1, j, 0] + self.ttgt[i, j - 1, 0]+ self.ttgt[i, j + 1, 0] + self.ttgt[i + 1, j, 0]) / 4.0self.ttgt[i, j, 1] = (self.tgrad[i, j, 1] + self.ttgt[i - 1, j, 1] + self.ttgt[i, j - 1, 1]+ self.ttgt[i, j + 1, 1] + self.ttgt[i + 1, j, 1]) / 4.0self.ttgt[i, j, 2] = (self.tgrad[i, j, 2] + self.ttgt[i - 1, j, 2] + self.ttgt[i, j - 1, 2]+ self.ttgt[i, j + 1, 2] + self.ttgt[i + 1, j, 2]) / 4.0return 0@ti.kerneldef error_kernel(self) -> int: # 用于計算誤差的核函數ti.loop_config(parallelize=self.parallelize, block_dim=self.block_dim) # 配置并行化和塊大小參數for i, j in self.tmask: # 使用嵌套的for循環遍歷tmask字段中非零值的索引 (i, j)些索引表示修復區域中需要進行計算誤差的像素if self.tmask[i, j] > 0: # 首先判斷當前像素位置 (i, j) 是否在修復區域內self.tmp[i, j, 0] = ti.abs( # 如果在修復區域內,則根據誤差計算公式計算每個顏色通道的誤差值self.tgrad[i, j, 0] + self.ttgt[i - 1, j, 0] +self.ttgt[i, j - 1, 0] + self.ttgt[i, j + 1, 0] +self.ttgt[i + 1, j, 0] - 4.0 * self.ttgt[i, j, 0])self.tmp[i, j, 1] = ti.abs(self.tgrad[i, j, 1] + self.ttgt[i - 1, j, 1] +self.ttgt[i, j - 1, 1] + self.ttgt[i, j + 1, 1] +self.ttgt[i + 1, j, 1] - 4.0 * self.ttgt[i, j, 1])self.tmp[i, j, 2] = ti.abs(self.tgrad[i, j, 2] + self.ttgt[i - 1, j, 2] +self.ttgt[i, j - 1, 2] + self.ttgt[i, j + 1, 2] +self.ttgt[i + 1, j, 2] - 4.0 * self.ttgt[i, j, 2])else: # 如果不在修復區域內(即掩碼為零),則將誤差值設置為0self.tmp[i, j, 0] = self.tmp[i, j, 1] = self.tmp[i, j, 2] = 0.0self.terr[0] = self.terr[1] = self.terr[2] = 0ti.loop_config(parallelize=self.parallelize, block_dim=self.block_dim)for i, j, k in self.tmp:self.terr[k] += self.tmp[i, j, k]return 0
# 用于執行迭代步驟并返回結果def step(self, iteration: int) -> Tuple[np.ndarray, np.ndarray]:for _ in range(iteration):self.iter_kernel() # 更新目標圖像的值self.error_kernel() # 計算最終的誤差tgt = self.ttgt.to_numpy()[:self.orig_N, :self.orig_M] # 將目標圖像ttgt轉換為NumPy數組tgt[tgt < 0] = 0tgt[tgt > 255] = 255 # 確保像素值范圍在 0 到 255 之間return tgt, self.terr.to_numpy() # 返回修復后的目標圖像數組 tgt 和誤差數組3. 算法總結
????????Fast Poisson Image Editing 是一個用于圖像編輯的算法,它的核心思想是通過求解泊松方程來進行圖像修復。
4. 代碼運行
4.1 測試
(1)由data.py代碼中download函數可以知道如何通過鏈接下載圖片并指定文件名。

?(2)通過操作可以在data文件下得到三張圖:
(3)?輸入命令行:
fpie -s test3_src.jpg -m test3_mask.jpg -t test3_tgt.jpg -o result3.jpg -h1 100 -w1 100 -n 5000 -g max
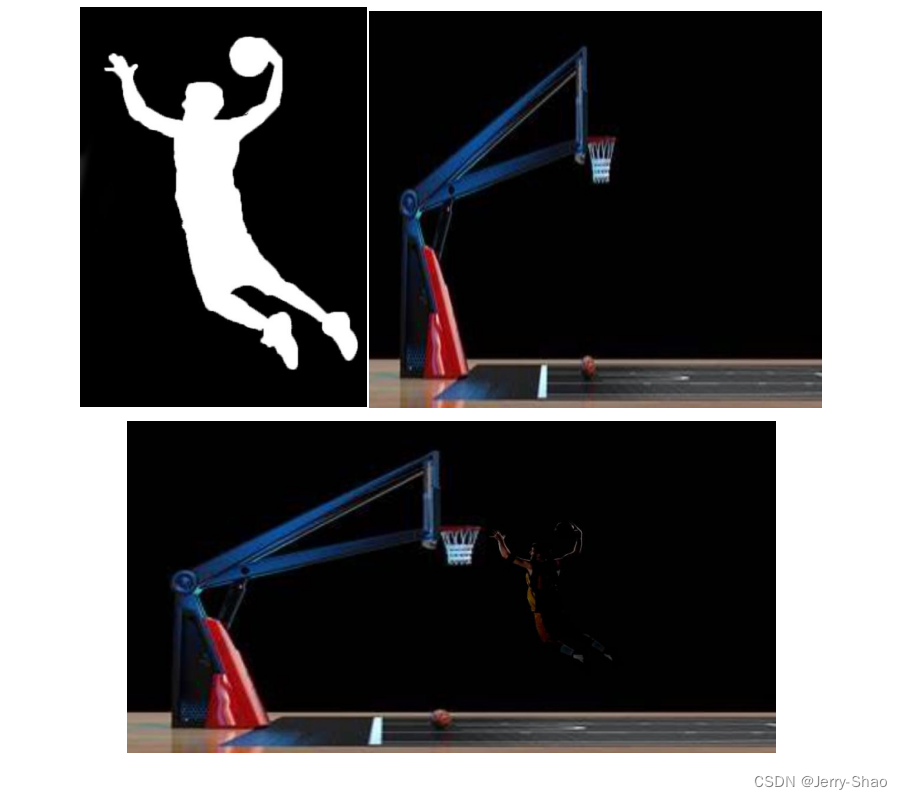
(4)運行后得到結果圖:
以下圖片為我們隨機在網上找的圖片,并進行編輯,非自帶圖片

4.2?基于GUI后端自定義框輸出編輯圖像結果
4.2.1?下載open-cv
pip install opencv-python
4.2.2?輸入命令
fpie-gui -s test1_src.jpg -t test1_target.jpg -o result.jpg -b taichi-cpu -n 10000
以下圖片為我們隨機在網上找的圖片,并進行編輯,非自帶圖片。

4.2.3?自定義框
在source中框出物品,再在target中點擊要嵌入的位置,最后result會產生結果。


(答案版))





)

、文件(File)和IO - 復習章節)


)

)

ADP5360ACBZ-1-R7 電量計 電池管理IC,ADP5072ACBZ 雙通道直流開關穩壓器,ADL5903ACPZN 射頻檢測器)

