通常，我們可以通過觀察畫出近似的波德圖，而不需要大量雜亂的代數和不可避免的相關代數錯誤。使用這種方法可以對電路的工作原理有很大的了解。在不同頻率下，哪些元件主導電路響應變得很清楚，因此合適的近似變得很明顯。可以直接得到轉折頻率和漸近線的近似解析表達式。可以構造相當復雜的網絡的阻抗和傳遞函數。因此，可以獲得洞察力，以便設計工程師可以修改電路以獲得所需的頻率響應。

圖形構造方法，也被稱為“在圖上做代數”，涉及使用一些簡單的規則來組合阻抗和傳遞函數的幅值波德圖。

3.1串聯阻抗：漸近線的加法

串聯連接表示阻抗的增加。如果單個阻抗幅值的波德圖是已知的，那么通過簡單地取單個阻抗漸近線中的最大值就可以求出串聯組合的漸近線。在許多情況下，結果是精確的。在其他情況下，例如當個別漸近線具有相同的斜率時，則結果是近似值；盡管如此，這種近似法的精確度還是相當不錯的。

考慮如下圖所示的串聯R-C網絡。

需要構造總串聯阻抗Z(s)的幅值漸近線，其中：

讓我們先畫出各個阻抗的大小。10 Ω電阻器的阻抗值為10 Ω?20 dBΩ。該值與頻率無關，如下圖8.41所示。

電容器的阻抗值為1/ωC。這個量與ω成反比，因此它的幅值波德圖是一個斜率為- 20 dB/十倍頻程的直線。線在角頻率ω處通過1 Ω?0 dBΩ，其中：

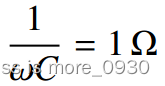
即，在：

用頻率f表示，它發生在：

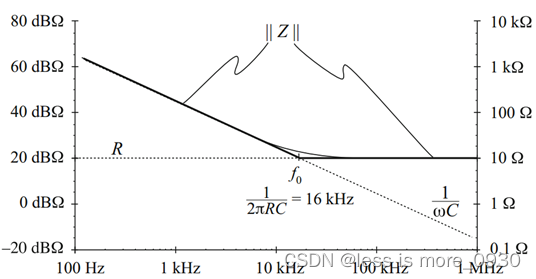
故電容阻抗幅值是一條斜率為-20dB/十倍頻程的線，在159kHz時通過0dBΩ，如下圖所示。
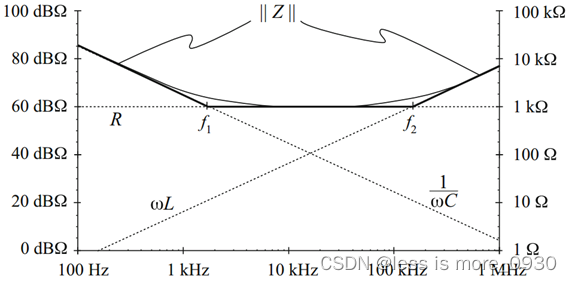
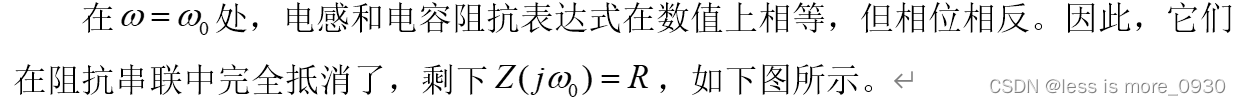