[數據結構1.0]快速排序

最近學習了快速排序，鼠鼠俺來做筆記了！

本篇博客用排升序為例介紹快速排序！

1.快速排序

快速排序是Hoare于1962年提出的一種二叉樹結構的交換排序方法，其基本思想為：任取待排序元素序列中的某元素作為基準值，按照該排序碼將待排序集合分割成兩子序列，左子序列中所有元素均小于基準值，右子序列中所有元素均大于基準值，然后最左右子序列重復該過程，直到所有元素都排列在相應位置上為止。

如果對上面的介紹蒙圈的話，沒關系，我們繼續看下面的內容，會仔細介紹的！

1.1.快速排序的”單趟“

快速排序的”單趟“簡單來說就是在需排序亂序數組中任取一個元素作為基準值，經過”單趟“過后，大于或者等于基準值的元素都排在基準值的后面，小于或者等于基準值的元素都排在基準值的前面，也就是說基準值所在的位置就是它應該出現的位置，這個基準值就排好了！

對于”單趟“的實現方法有但不限于下面三種：

1.1.1.hoare版本

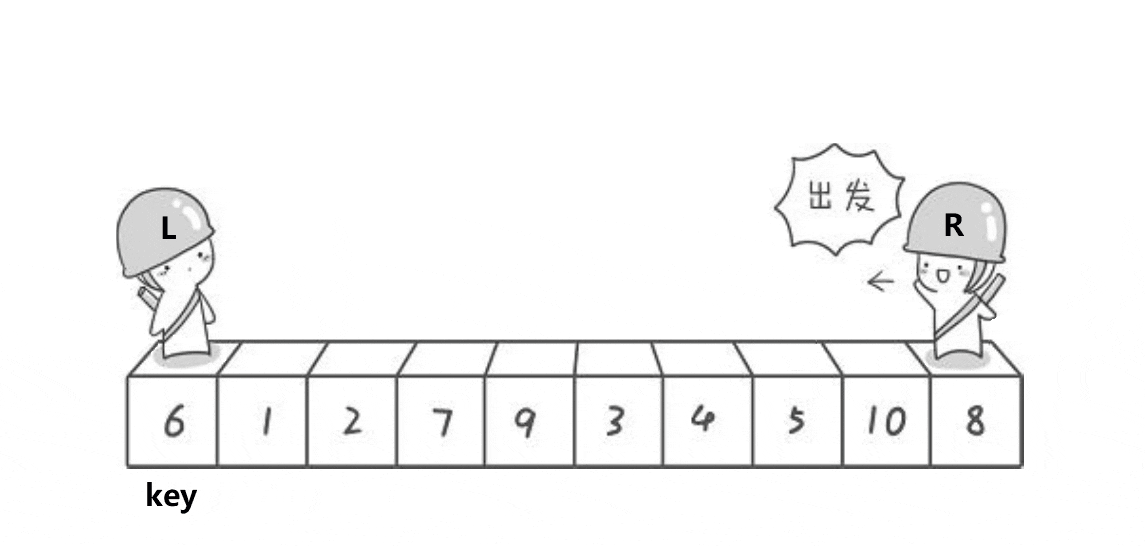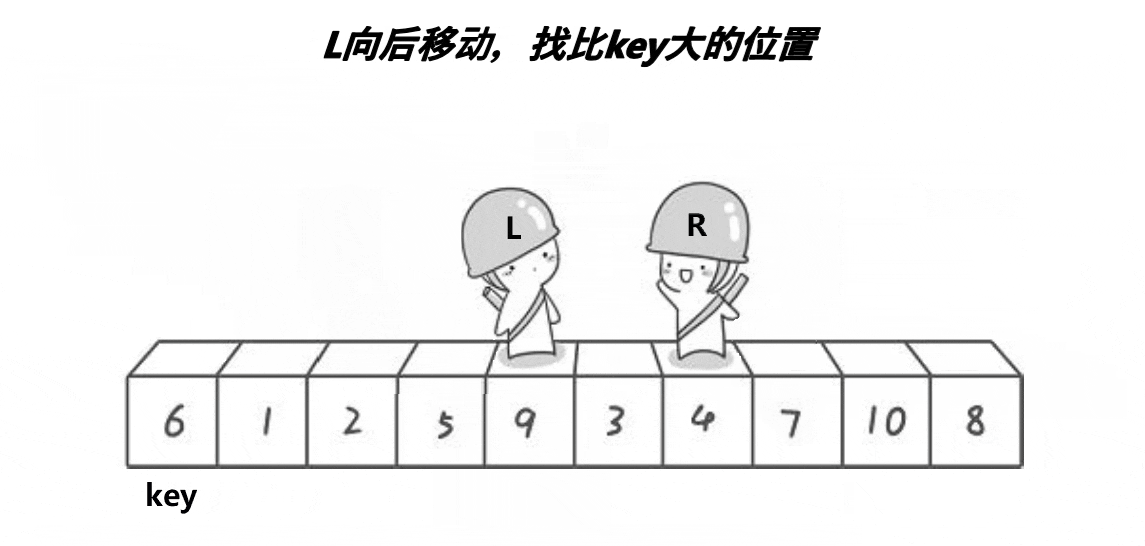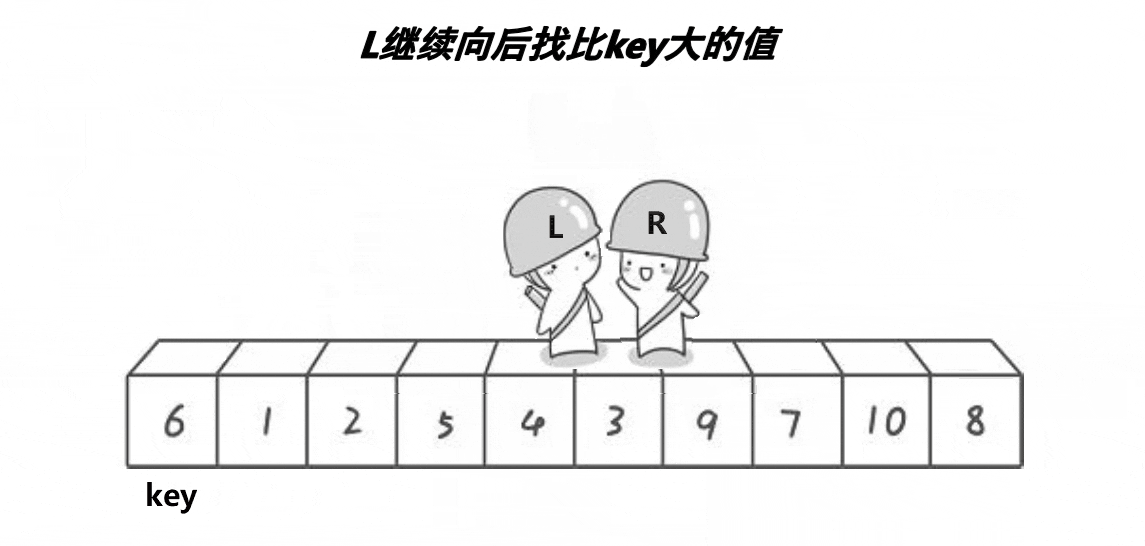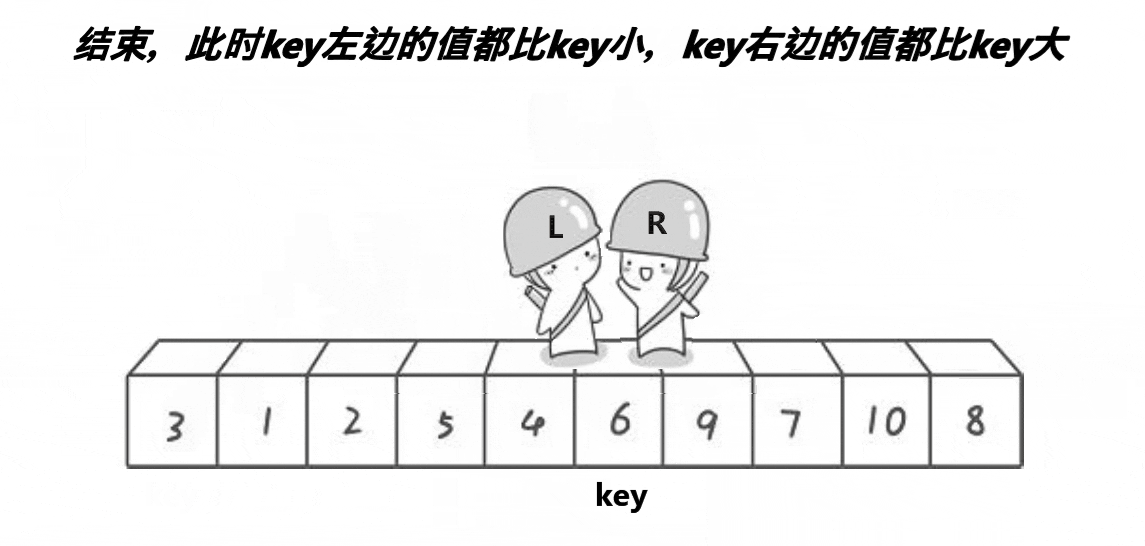
這個動圖就是hoare版本的”單趟“實現方法！這里取第一個元素6為基準值；R從最”右邊“開始找比基準值小的元素，L從最”左邊“開始找比基準值大的元素，?然后交換下標為R和L的元素；R繼續找比基準值小的元素，L繼續找比基準值大的元素，再交換下標為R和L的元素…………直到R和L相遇，將基準值和相遇位置的元素即可！

其實這個本質就是將比基準值大的元素”甩“到”后面“，將比基準值小的元素”甩“到”前面“。

也許會有疑問，怎么保證相遇位置的元素一定不大于基準值呢？

因為只要是R先動，L后動的話必然能保證相遇的元素一定不大于基準值！

相遇無非兩種情況：

1.R遇L：R在去找小于基準值的元素的過程中，下標為L的元素必然是不大于基準值的元素。當R去找小于基準值的元素沒有找到卻遇到L時，那么相遇位置的值就是不大于基準值的元素。

2.L遇R：由于R先動，那么L在找大于基準值的元素的過程中，下標為R的元素必然是不大于基準值的元素。當L去找大于基準值的元素沒有找到卻遇到R時，那么相遇位置的值就是不大于基準值的元素。

?hoare版本的“單趟”代碼如下，需排序亂序數組下標為begin—end：

//hoare版本int keyi = begin;int left = begin, right = end;while (left < right){while (left < right && a[right] >= a[keyi]){right--;}while (left < right && a[left] <= a[keyi]){left++;}Swap(&a[left], &a[right]);}Swap(&a[keyi], &a[right]);keyi = right;

由于hoare版本寫起來很容易出錯誤，所以我們一般寫下面兩種版本！

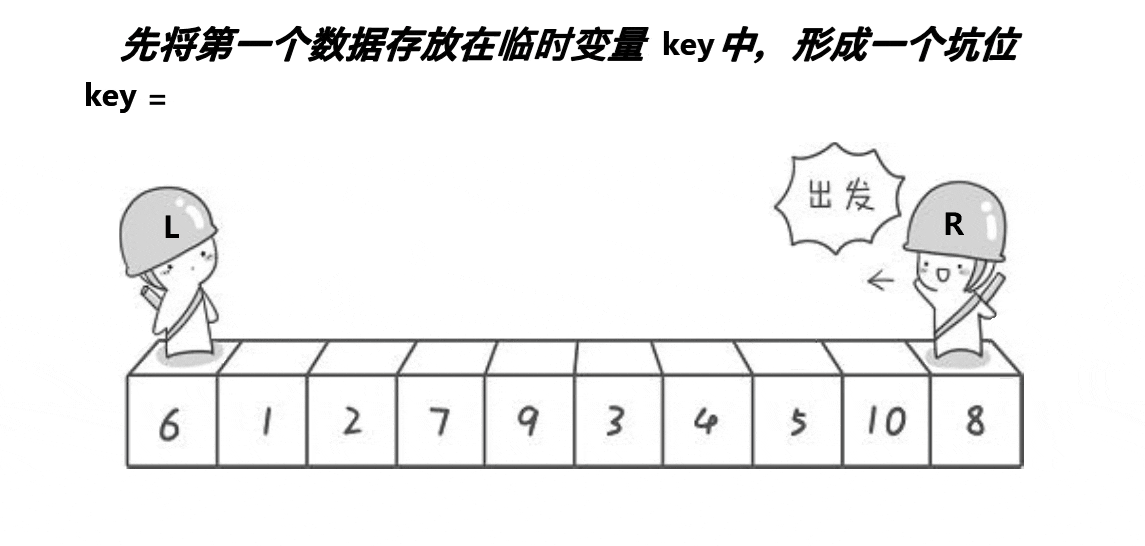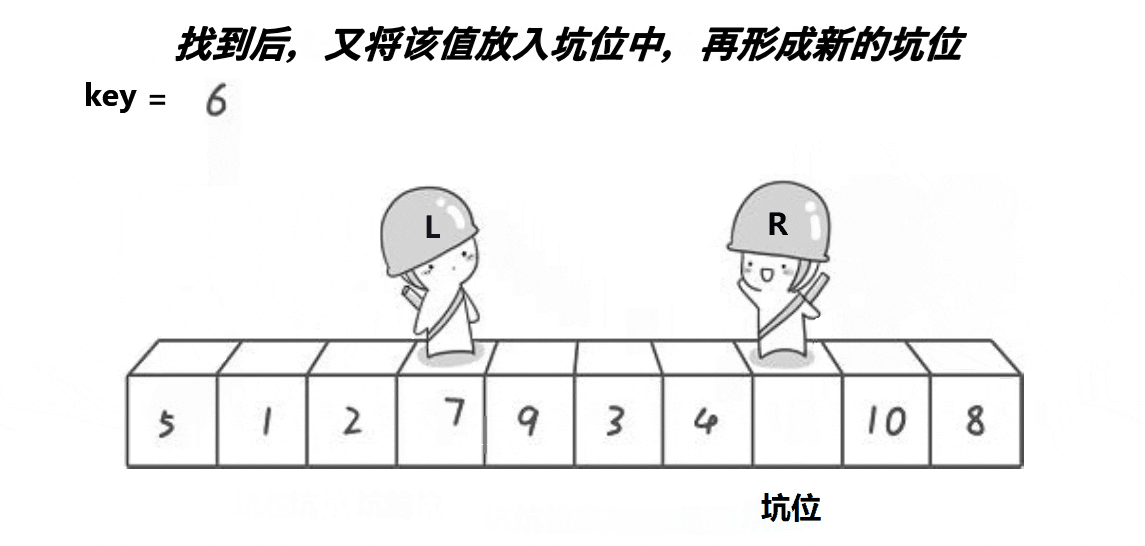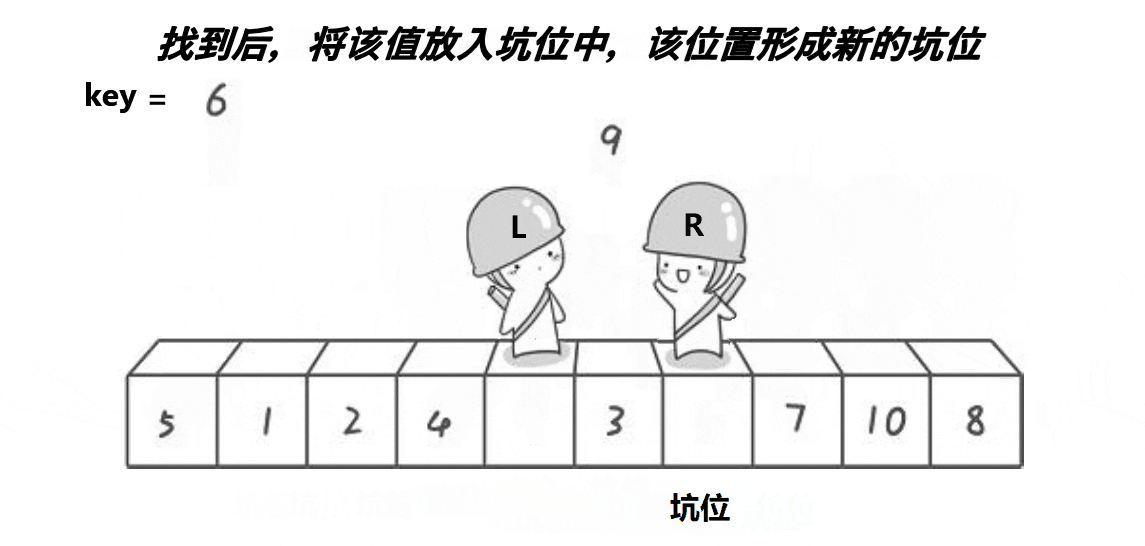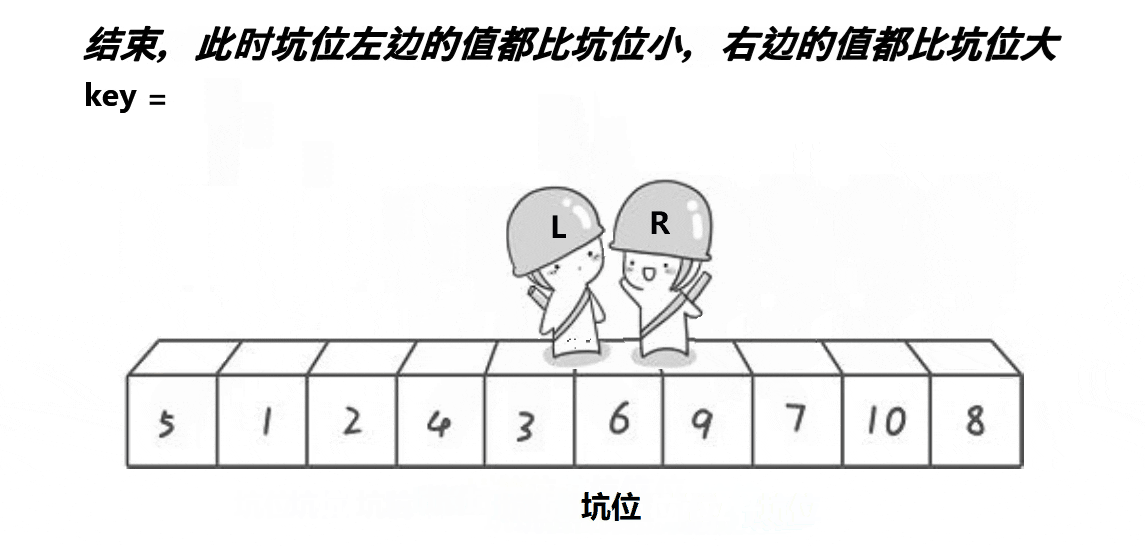
1.1.2.挖坑法版本

也是取第一個元素6為基準值。初始坑位設置為基準值下標。讓R從最“右邊”開始找比基準值小的元素，找到后將下標為R的元素填入坑位，那么新的坑位就變成了R；讓L從最“左邊”開始找比基準值大的元素，找到后將下標為L的元素填入坑位，那么新的坑位就變成了L；R再找比基準值小的元素……直到R和L相遇，將基準值填入坑位即可。

本質就是R找小填入“左邊”坑位，L找大填入“右邊”坑位，最后一個坑位必定是R和L相遇位置，填入基準值就好。

挖坑法版本“單趟”代碼如下，需排序亂序數組下標為begin—end：

//挖坑法版本int  key=a[begin];int left = begin, right = end;int hole = begin;while (left < right){while (left < right && a[right] >= key){right--;;}a[hole] = a[right];hole = right;while (left < right && a[left] <= key){left++;}a[hole] = a[left];hole = left;}a[hole] = key;int keyi = hole;

1.1.3.前后指針版本

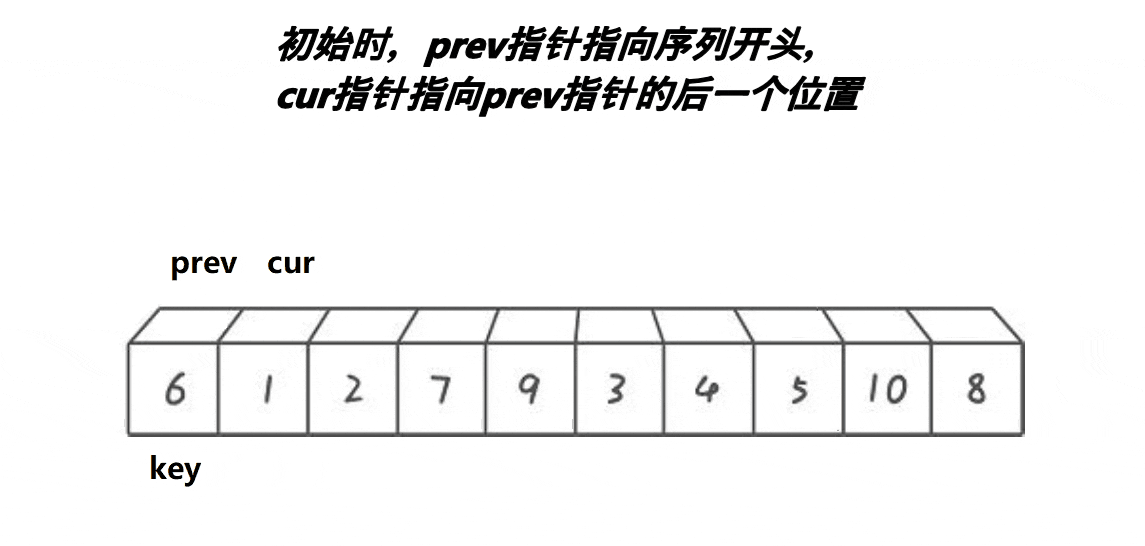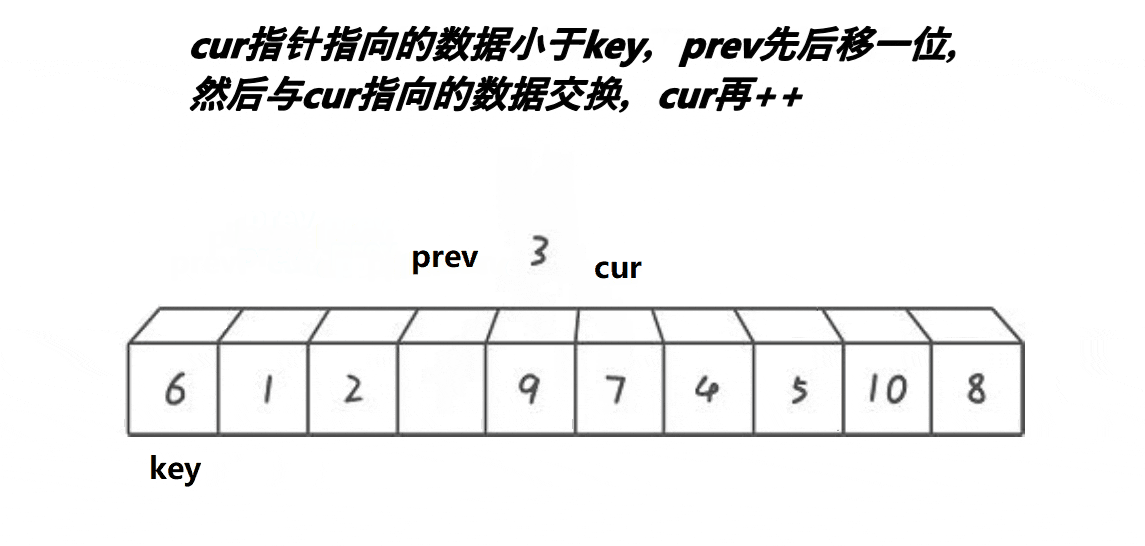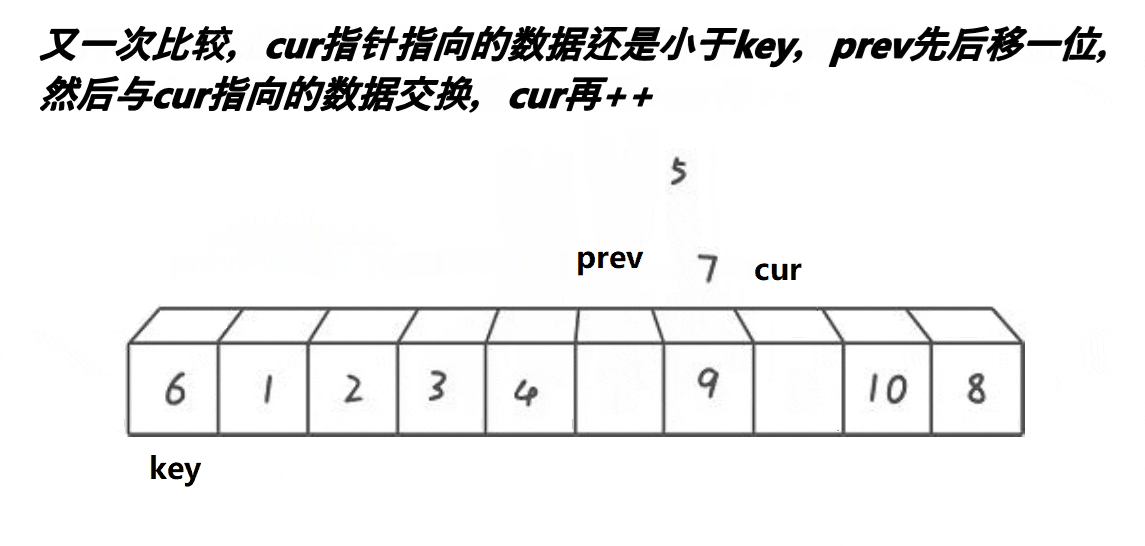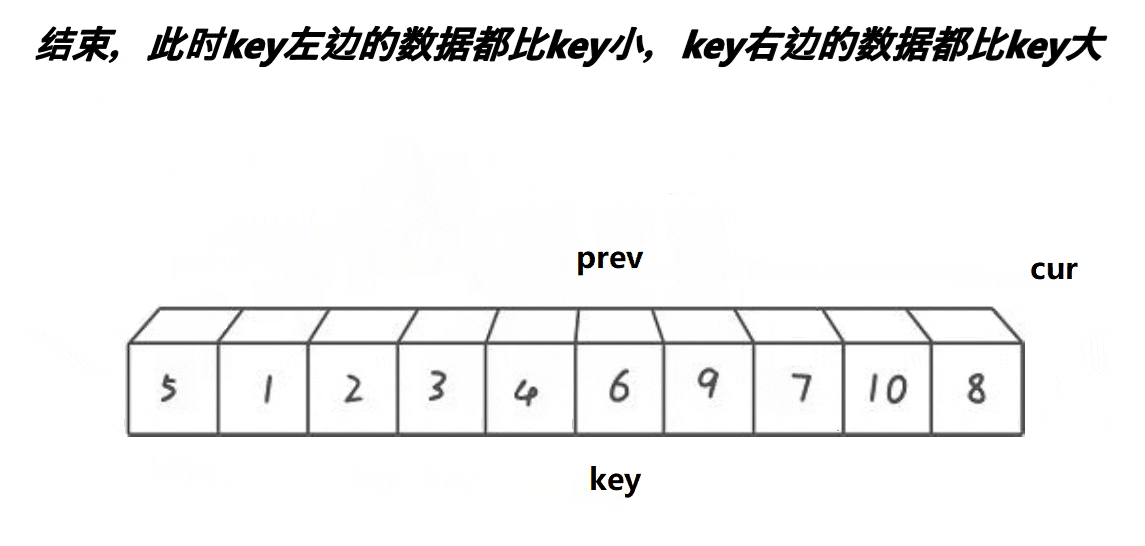
取第一個元素6為基準值。prev初始指向基準值，cur初始指向基準值的下一個元素。cur遍歷數組：如果cur遇到大于基準值的元素，++cur；否則++prev、cur指向的元素和prev指向的元素交換、++cur。

前后指針版本“單趟”代碼如下，需排序亂序數組下標為begin—end：

//前后指針版本int cur = begin + 1, prev = begin;int keyi = begin;while (cur <= end){if (a[cur] > a[keyi]){++cur;}else{++prev;Swap(&a[prev], &a[cur]);++cur;}}Swap(&a[keyi], &a[prev]);keyi = prev;

這里指針寫成了下標的形式，思想沒變，本質上還是一樣的！

1.2.快速排序的遞歸寫法?

經過“單趟”過后，被選中的基準值就排在了它該出現的位置，就是說當數組排好變得有序后，基準值就在“單趟”過后出現的位置！

既然基準值已經拍好了，如果基準值的“左邊”的元素集合能有序并且基準值的“右邊”的元素集合能有序，那么需排序的亂序數組就排好了，變得有序了。舉個例子：

如圖，所以說快速排序一種二叉樹結構的交換排序方法。進行“單趟”排好基準值，遞歸“左邊”元素集合…………“左邊”元素集合排好后，遞歸“右邊”元素集合…………“右邊”元素集合排好后就搞定了！

遞歸結束條件：當元素集合只有1個值或為空。

看看快速排序的遞歸寫法代碼：

void QuickSort(int* a, int begin, int end)
{if (begin >= end){return;}//hoare版本/*int keyi = begin;int left = begin, right = end;while (left < right){while (left < right && a[right] >= a[keyi]){right--;}while (left < right && a[left] <= a[keyi]){left++;}Swap(&a[left], &a[right]);}Swap(&a[keyi], &a[right]);keyi = right;*///挖坑法版本int  key=a[begin];int left = begin, right = end;int hole = begin;while (left < right){while (left < right && a[right] >= key){right--;;}a[hole] = a[right];hole = right;while (left < right && a[left] <= key){left++;}a[hole] = a[left];hole = left;}a[hole] = key;int keyi = hole;//前后指針版本/*int cur = begin + 1, prev = begin;int keyi = begin;while (cur <= end){if (a[cur] > a[keyi]){++cur;}else{++prev;Swap(&a[prev], &a[cur]);++cur;}}Swap(&a[keyi], &a[prev]);keyi = prev;*/QuickSort(a, begin, keyi - 1);QuickSort(a, keyi + 1, end);
}

我們試試這個快速排序：

#define _CRT_SECURE_NO_WARNINGS
#include<stdio.h>void PrintArrar(int* a, int n)
{for (int i = 0; i < n; i++){printf("%d ", a[i]);}printf("\n");
}void Swap(int* a, int* b)
{int tmp = *a;*a = *b;*b = tmp;
}void QuickSort(int* a, int begin, int end)
{if (begin >= end){return;}//hoare版本/*int keyi = begin;int left = begin, right = end;while (left < right){while (left < right && a[right] >= a[keyi]){right--;}while (left < right && a[left] <= a[keyi]){left++;}Swap(&a[left], &a[right]);}Swap(&a[keyi], &a[right]);keyi = right;*///挖坑法版本/*int  key=a[begin];int left = begin, right = end;int hole = begin;while (left < right){while (left < right && a[right] >= key){right--;;}a[hole] = a[right];hole = right;while (left < right && a[left] <= key){left++;}a[hole] = a[left];hole = left;}a[hole] = key;int keyi = hole;*///前后指針版本int cur = begin + 1, prev = begin;int keyi = begin;while (cur <= end){if (a[cur] > a[keyi]){++cur;}else{++prev;Swap(&a[prev], &a[cur]);++cur;}}Swap(&a[keyi], &a[prev]);keyi = prev;QuickSort(a, begin, keyi - 1);QuickSort(a, keyi + 1, end);
}int main()
{int a[] = { 9,8,5,47,6,3,2,10 };PrintArrar(a, sizeof(a) / sizeof(a[0]));QuickSort(a, 0, sizeof(a) / sizeof(a[0]) - 1);PrintArrar(a, sizeof(a) / sizeof(a[0]));return 0;
}

沒問題的：

1.3.快速排序的非遞歸寫法

鼠鼠這里介紹一種快速排序的非遞歸寫法。

需要用到鼠鼠前面博客?介紹的棧，利用到棧寫的快速排序沒有用到遞歸但思想卻很像遞歸！

?非遞歸寫法思想如上圖。我們看快速排序非遞歸代碼如下，其中變量s是棧。鼠鼠這里“單趟”選擇挖坑法版本，當然老爺們可以用其他版本：

void QuickSortNonr(int* a, int begin, int end)
{Stack s;StackInit(&s);StackPush(&s, end);StackPush(&s, begin);while (!StackEmpty(&s)){int start = StackTop(&s);StackPop(&s);int finish = StackTop(&s);StackPop(&s);int  key = a[start];int left = start, right = finish;int hole = start;while (left < right){while (left < right && a[right] >= key){right--;;}a[hole] = a[right];hole = right;while (left < right && a[left] <= key){left++;}a[hole] = a[left];hole = left;}a[hole] = key;if (start < left - 1){StackPush(&s, left - 1);StackPush(&s, start);}if (left + 1 < finish){StackPush(&s, finish);StackPush(&s, left + 1);}}StackDestroy(&s);
}

我們要用到棧，所以記得將我們自己寫的棧的頭文件和源文件拷貝一份到快速排序的工程目錄下?，再包棧的頭文件就可以用了。我們試試：

#define _CRT_SECURE_NO_WARNINGS
#include<stdio.h>
#include"Stack.h" //注意包含棧的頭文件void PrintArrar(int* a, int n)
{for (int i = 0; i < n; i++){printf("%d ", a[i]);}printf("\n");
}void QuickSortNonr(int* a, int begin, int end)
{Stack s;StackInit(&s);StackPush(&s, end);StackPush(&s, begin);while (!StackEmpty(&s)){int start = StackTop(&s);StackPop(&s);int finish = StackTop(&s);StackPop(&s);int  key = a[start];int left = start, right = finish;int hole = start;while (left < right){while (left < right && a[right] >= key){right--;;}a[hole] = a[right];hole = right;while (left < right && a[left] <= key){left++;}a[hole] = a[left];hole = left;}a[hole] = key;if (start < left - 1){StackPush(&s, left - 1);StackPush(&s, start);}if (left + 1 < finish){StackPush(&s, finish);StackPush(&s, left + 1);}}StackDestroy(&s);
}int main()
{int a[] = { 9,8,5,47,6,3,2,10 };PrintArrar(a, sizeof(a) / sizeof(a[0]));QuickSortNonr(a, 0, sizeof(a) / sizeof(a[0]) - 1);PrintArrar(a, sizeof(a) / sizeof(a[0]));return 0;
}

?沒問題吧！

2.快速排序遞歸寫法優化?

2.1.三數取中法選基準值

對于遞歸寫法來說，對于需排序數組本身就是升序或者降序的情況適應的不是很好，因為：

1.固定了選擇元素集合第一個元素為基準值，每次“單趟”過后都會導致某一邊元素集合為空的情況。這樣的話如果本身就是升序或者降序的需排序數組個數有n個的話，就要遞歸n層，很容易棧溢出！

2.每次“單趟”時間復雜度是O(N)，遞歸n層的話快速排序時間復雜度是O(N^2)，時間效率不劃算！

所以我們有三數取中選基準值，我們取元素集合第一個元素、最后一個元素和中間那個元素，這三個元素比較得出第二大的元素，將這個元素與元素集合第一個元素交換再進行“單趟”。

這樣的話就能很好適應需排序數組本身就是升序或者降序的情況，因為這樣經過“單趟”之后，基準值一定會出現在“中間”。這樣子去遞歸的話，每一層遞歸都會被“二分”，遞歸層數大大減少，遞歸log(N)層就行！

加入了三數取中選基準值的遞歸寫法的快速排序時間復雜度是O(N*logN)。

而且加入了三數取中選基準值的遞歸寫法的快速排序對于需排序數組本身不是升序或者降序的情況一樣有幫助，可以讓每層遞歸盡量“二分”，從而減少遞歸層數！

三數取中法代碼：

int GetMidi(int* a, int begin, int end)
{int midi = begin + (end - begin) / 2;if (a[begin] > a[midi]){if (a[begin] > a[end]){if (a[midi] > a[end]){return midi;}elsereturn end;}else{return begin;}}else{if (a[midi] > a[end]){if (a[end] > a[begin]){return end;}else{return begin;}}else{return midi;}}
}

當沒有加入三數取中選基準值的遞歸寫法的快速排序排10000個升序元素組成的數組時，在Debug環境下就會崩潰，棧溢出了：

#define _CRT_SECURE_NO_WARNINGS
#include<stdio.h>
#include<stdlib.h>
#include<time.h>int GetMidi(int* a, int begin, int end)
{int midi = begin + (end - begin) / 2;if (a[begin] > a[midi]){if (a[begin] > a[end]){if (a[midi] > a[end]){return midi;}elsereturn end;}else{return begin;}}else{if (a[midi] > a[end]){if (a[end] > a[begin]){return end;}else{return begin;}}else{return midi;}}
}void Swap(int* a, int* b)
{int tmp = *a;*a = *b;*b = tmp;
}void QuickSort(int* a, int begin, int end)
{if (begin >= end){return;}//三數取中選基準值/*int midi = GetMidi(a, begin, end);Swap(&a[begin], &a[midi]);*///前后指針版本int cur = begin + 1, prev = begin;int keyi = begin;while (cur <= end){if (a[cur] > a[keyi]){++cur;}else{++prev;Swap(&a[prev], &a[cur]);++cur;}}Swap(&a[keyi], &a[prev]);keyi = prev;QuickSort(a, begin, keyi - 1);QuickSort(a, keyi + 1, end);
}int main()
{int n = 10000;int* a = (int*)malloc(sizeof(int) * n);srand((unsigned int)time(0));a[0] = rand();for (int i = 1; i < n ; i++){a[i] = a[i-1] + 1;}int begin = clock();QuickSort(a, 0, n - 1);int end = clock();printf("%d\n", end - begin);return 0;
}

結果：

當加入三數取中選基準值的遞歸寫法的快速排序，排100w個升序元素組成的數組都沒問題，Debug環境下：

#define _CRT_SECURE_NO_WARNINGS
#include<stdio.h>
#include<stdlib.h>
#include<time.h>int GetMidi(int* a, int begin, int end)
{int midi = begin + (end - begin) / 2;if (a[begin] > a[midi]){if (a[begin] > a[end]){if (a[midi] > a[end]){return midi;}elsereturn end;}else{return begin;}}else{if (a[midi] > a[end]){if (a[end] > a[begin]){return end;}else{return begin;}}else{return midi;}}
}void Swap(int* a, int* b)
{int tmp = *a;*a = *b;*b = tmp;
}void QuickSort(int* a, int begin, int end)
{if (begin >= end){return;}//三數取中選基準值int midi = GetMidi(a, begin, end);Swap(&a[begin], &a[midi]);//前后指針版本int cur = begin + 1, prev = begin;int keyi = begin;while (cur <= end){if (a[cur] > a[keyi]){++cur;}else{++prev;Swap(&a[prev], &a[cur]);++cur;}}Swap(&a[keyi], &a[prev]);keyi = prev;QuickSort(a, begin, keyi - 1);QuickSort(a, keyi + 1, end);
}int main()
{int n = 1000000;int* a = (int*)malloc(sizeof(int) * n);srand((unsigned int)time(0));a[0] = rand();for (int i = 1; i < n ; i++){a[i] = a[i-1] + 1;}int begin = clock();QuickSort(a, 0, n - 1);int end = clock();printf("%d\n", end - begin);return 0;
}