1.深度學習花書前言
??機器學習早期的時候十分依賴于已有的知識庫和人為的邏輯規則,需要人們花大量的時間去制定合理的邏輯判定,可以說是有多少人工,就有多少智能。后來逐漸發展出一些簡單的機器學習方法例如logistic regression、naive bayes等,機器可以通過一些特征來學習一定的模式出來,但這非常依賴于可靠的特征,比如對于logistic regression用來輔助醫療診斷,我們無法將核磁共振圖像直接輸入機器來作出診斷,而是醫生需要先做一份報告總結一些特征,而機器通過報告中提供的表征再來進行機器學習,這就對如何提取有效表征提出了很大的要求,仍是一個需要花費很多人力的過程。鑒于這些簡單模型只能從專家提供的表征映射到結果,而不能自己提取出特征的局限性,人們發展出了表征學習(representation learning),希望機器自己能夠提取出有意義的特征而無需人為干預。經典的例子就是Autoencoder,主要就是由加碼器encoder從原始數據提取特征,然后可以通過解碼器decoder利用新的表征來重塑原始數據。
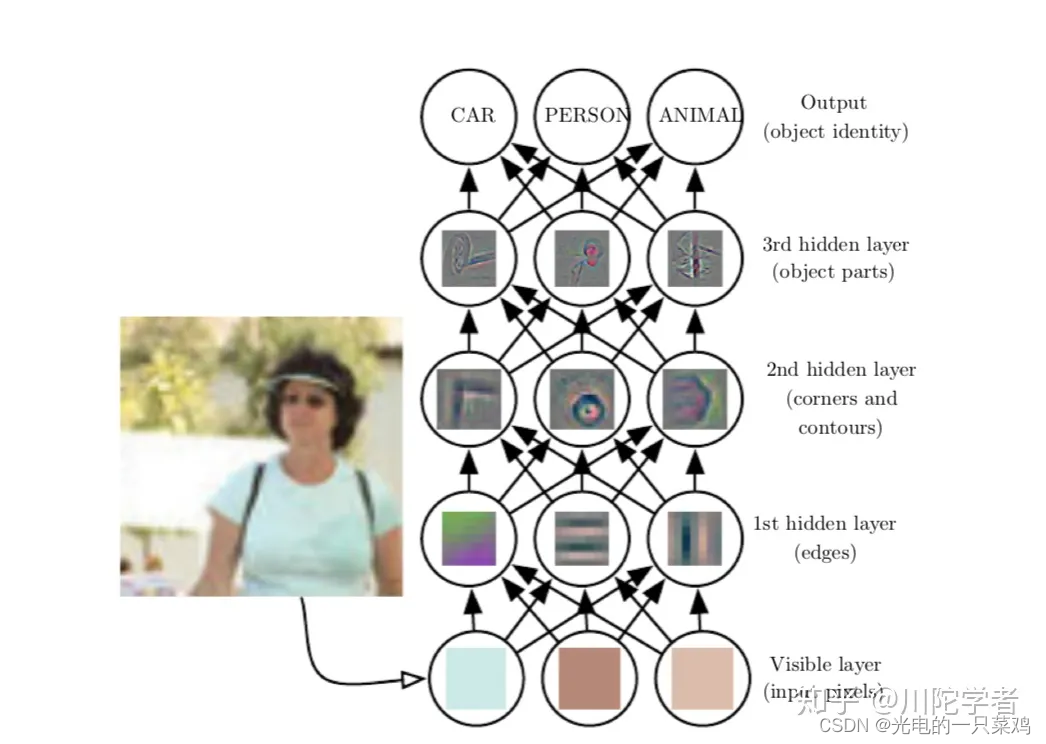
??這些表征很有可能是隱含的、抽象的,比如圖像識別中單個像素可能沒有有效的信息,更有意義的是若干像素組成的邊,由邊組成的輪廓,進而由輪廓組成的物體。深度學習就是通過一層層的表征學習,每層可能邏輯很簡單,但之后的層可以通過對前面簡單的層的組合來構建更復雜的表征。經典的例子如多層感知機(multilayer perceptron),就是每個感知機的數理邏輯都很簡單,層內可以并行執行,層間順序執行,通過層層疊加實現更復雜的邏輯。深度學習的“深”可以理解為通過更多層來結合出更復雜的邏輯,這就完成了從輸入到內在層層表征再由內在表征到輸出的映射。
花書可以大致分為三大部分:
- 機器學習基礎知識:涵蓋線性代數,概率論,數值計算和傳統機器學習基礎等知識。如果之前學過Andrew Ng的CS229的話基本可以跳過。
- 深度神經網絡核心知識:屬于本書必讀部分,涵蓋前饋神經網絡,卷積神經網絡(CNN),遞歸神經網絡(RNN) 等。
- 深度學習前沿:有一些前沿研究領域的介紹,如線性因子模型,表征學習,生成模型等。
??在1940-1960年間,人們更多的是從神經科學找靈感,希望能夠搭建能夠模擬人腦工作模式的神經網絡,這個時期的名字是人工神經網絡(Artificial Neural Network) 或神經機械學(cybernetics)。感知機模型(perceptron)也是這個時期的產物。這個時期的模型大部分都是線性模型,對于非線性的關系不能進行很好的模擬所以有很大的局限性,深度學習研究就逐漸降溫了。不過,這個時期為后來的深度學習打下基礎,我們現在訓練常用的隨機梯度下降算法(stochastic gradient descent)就是源自處理這個時期的一種線性模型——自適應線性單元(Adaptive Linear Neuron)。雖然現在仍有媒體經常將深度學習與神經科學類比,但是由于我們對大腦工作機制的研究進展緩慢,所以實際上現在深度學習從業者已很少從神經科學中尋找靈感。
??第二個階段是1980-1990年代,這個時候更多的稱為聯結主義(connectionism)或并行分布式計算(parallel distributed computing),主要是強調很多的簡單的計算單位可以通過互聯進行更復雜的計算。這個時期成果很多,比如現在常用的反向傳播算法(back propagation)還有自然語言處理中常用的LSTM(第十章講遞歸神經網絡時詳談)都來自與這個時期。之后由于很多AI產品期望過高而又無法落地,研究熱潮逐漸退去。
??第三個階段就是2006年至今,由于軟硬件性能的提高,深度學習逐漸應用在各個領域,深度學習研究重整旗鼓。“深度”學習的名字成為主流,意在強調可以訓練更多層次更復雜的神經網絡,“深”幫助我們開發更復雜的模型,解決更復雜的問題。
??先說數據大小,如果自己動手訓練過深度學習模型的話就會體驗到數據集大小對預測準確率影響很大,即使是同一個模型,訓練量的大小不同會造成最終效果天差地別,統計學上,通過小量數據訓練延展到新數據是很困難的。隨著世界數字化的趨勢大數據的發展,我們有更多被標注的數據集,深度學習模型的準確度也因此受益。
??隨著模型準確度的提高,深度學習也逐漸得到更廣泛的實際應用,比如圖像識別,語音識別,機器翻譯等領域。像DeepMind AlphaGo這種強化學習方面的應用更是掀起了全民AI熱潮。與此同時,各種深度學習框架的出現如Caffe,Torch,Tensorflow等也方便更多人學習或利用深度學習模型。這些反過來又促進了深度學習行業的發展。
??在一片繁榮下,深度學習的可解釋性又常受詬病,對抗樣本等的出現也讓人思考深度學習的有效性,這都需要更多從業者去深入思考,而不能滿足于黑箱成果,“路漫漫其修遠兮,吾將上下而求索。”
2.三要素
2.1任務
??在機器學習系統中,任務常常是通過已有的一些例子(example)來總結出一些統計規律。而每個例子又常常由很多通過測量得到的特征(feature)構成,我們常常將各個特征用特征向量來代表一個特征。機器學習任務可以大致分為以下的幾類問題:
??分類問題(classification): 指的是假如我們研究對象有k種不同的類別,我們希望程序能夠知道每個數據屬于哪一類,即學習的映射。比如圖像識別里,我們希望推斷一個圖片是小汽車還是飛機,還有人臉識別中我們希望知道這些臉部圖像屬于誰。
??回歸問題(regression):我們有的時候想用機器預測某一具體數值,即學習的映射。這個定義和分類問題有些類似,但是輸出格式不同。例子有我們想預測將來股票的價格的等。
??結構化輸出(structured output): 這是一個比較廣的類別,主要指輸出格式可能具有多個元素,并且各元素之間有較強關聯。比如字符識別問題(Optical Character Recognition,簡稱OCR),即通過程序將圖片中包含文字的部分識別出來并轉換成字符串;語音識別問題(speech recognition)輸入音頻通過程序轉化成相應的文字表示;機器翻譯(machine translation)將某種語言翻譯成另一種語言;圖像描述(image captioning)即輸入圖像輸出描述圖像的文字等。
??機器合成(synthesis):指機器通過已有的訓練數據集可以生成一些與數據集類似的數據,比如圖像合成語音合成等。
??這些分類并不是很嚴格的定義,對于同一個問題我們常常可以把它當做不同種類的問題而采取不同方法解決,比如推薦系統預測用戶是否會購買某種商品,我們既可以把它當做回歸問題,也可以當做二元分類問題。
2.2性能指標
??為了研究機器學習模型的有效性,我們需要可以定量的測量它的性能。比方說對于分類問題,我們可以定義準確率(accuracy)即在所有數據中模型做出正確分類的百分比,我們也可以測量錯誤率(error rate)即模型做出錯誤判斷的百分比,而模型的目的就是提高正確率或減小錯誤率。這里我們要引出測試集(test set)的概念,通常我們希望我們的模型不僅僅能描述已有的數據,而是對于新數據也能做出很好的預測,所以我們通常要利用一個獨立于訓練集的測試數據集來實測模型的性能指標。
??當然,對于某一研究對象找到合適的性能指標不一定是顯而易見的。比方說對于翻譯問題,我們的目標是整個句子都需正確,還是對于翻譯正確句子的某一部分也給部分獎勵?對于回歸問題,我們是更多懲罰很少出錯,但每次錯誤都是重大錯誤的系統,還是更多懲罰經常出錯但是都是中等程度錯誤的系統?這些都需要視應用而定。
2.3經驗
??依賴于我們提供給機器的數據集格式,我們可以大致將機器學習問題分為監督學習(supervised learning)和無監督學習(unsupervised learning)問題。
??監督學習:數據集不僅僅有特征,每個數據還有標簽(label)。比方說圖像識別數據里我們不僅提供原始圖像每個像素值,我們還標注每個圖像的類型,比如圖像是飛機還是汽車。
??無監督學習:相應地,在無監督學習里,數據只有特征,沒有標注的標簽,我們需要機器學習這個研究對象的概率分布,比如說聚類(clustering)問題,我們希望機器可以通過這些特征而把數據集分成不同的類似的群,比如通過用戶之前的購買記錄分析用戶的年齡段等。
??強化學習(reinforcement learning): 還有一類問題不一定有固定的靜態的數據集,而是通過與環境的不斷交互,形成機器學習系統與環境的反饋,從而不斷的改進模型,經典例子如DeepMind的AlphaGo。
3.欠擬合與過擬合的本質
??訓練機器學習模型的目的不僅僅是可以描述已有的數據,而且是對未知的新數據也可以做出較好的推測,這種推廣到新數據的能力稱作泛化(generalization)。我們稱在訓練集上的誤差為訓練誤差(training error),而在新的數據上的誤差的期望稱為泛化誤差(generalization error)或測試誤差(test error)。通常我們用測試集上的數據對模型進行測試,將其結果近似為泛化誤差。
??為什么我們只觀測了訓練集卻可以影響測試集上的效果呢?如果他們是完全隨機的無關的分布我們是無法做出這樣的推測的,我們通常需要做出對于訓練集和測試集的采樣過程的假設。訓練集和測試集是由某種數據生成分布產生的,通常我們假設其滿足獨立同分布(independent and identically distributed, 簡稱i.i.d),即每個數據是相互獨立的,而訓練集和測試集是又從同一個概率分布中取樣出來的。
??假設參數固定,那么我們的訓練誤差和測試誤差就應相同。但是實際上,在機器學習模型中,我們的參數不是事先固定的,而是我們通過采樣訓練集選取了一個僅優化訓練集的參數,然后再對測試集采樣,所以測試誤差常常會大于訓練誤差。
我們的機器學習模型因此有兩個主要目的:
盡量減小訓練誤差。
盡量減小訓練誤差和測試誤差間的間距
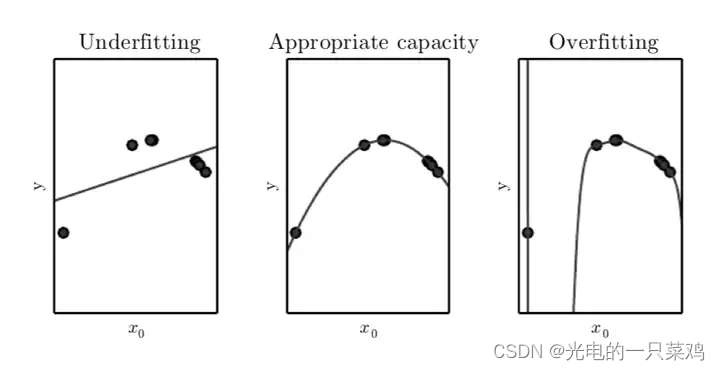
??模型是欠擬合還是過擬合是由模型的容量(capacity)決定的。低容量由于對訓練集描述不足造成欠擬合,高容量由于記憶過多訓練集信息而不一定對于測試集適用導致過擬合。比如對于線性回歸,它僅適合數據都在一條直線附近的情形,容量較小,為提高容量,我們可以引入多次項,比如二次項,可以描述二次曲線,容量較一次多項式要高。對如下圖的數據點,一次式容量偏小造成欠擬合,二次式容量適中擬合較好,而九次式容量偏大造成過擬合。
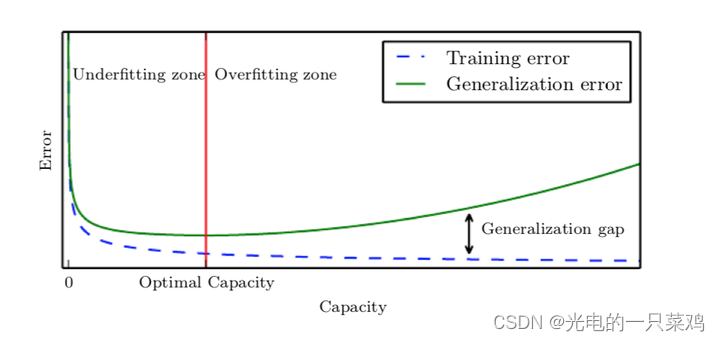
??訓練誤差,測試誤差和模型容量的關系可以由下圖表示,在容量較小時我們處在欠擬合區,訓練誤差和測試誤差均較大,隨著容量增大,訓練誤差會逐漸減小,但測試誤差與訓練誤差的間距也會逐漸加大,當模型容量超過最適容量后,測試誤差不降反增,進入過擬合區
4.正則化方法
??為了減小測試誤差與訓練誤差的差距過大防止過擬合,我們需要正則化方法(regularization),這一方法的主要目的是給模型進行一些修改使其傾向于減小測試誤差。
??假如我們引入一項對權重參數矢量w的正則項使得損失函數變為 J ( w ) = M S E t r a i n + λ w T w J(w)=MSE_{train}+{\lambda}w^Tw J(w)=MSEtrain?+λwTw。 λ {\lambda} λ等于零時它和原來的損失函數相同,當 λ {\lambda} λ越大時第二項造成的影響越大,為了使誤差函數更小,則需要使 w w w更小,如使每一個 w w w坐標更小或使 w w w更集中在某些特征上而其他特征上趨于零,我們需要通過調節 λ {\lambda} λ大小來找到過擬合與欠擬合間合適的平衡點。例如對于九次多項式擬合,如下圖所示,在最左圖中當 λ {\lambda} λ過大時,每一個多次項的 w w w都趨于零,曲線是一條近似直線,造成欠擬合,在最右圖中,當 λ {\lambda} λ趨于零時正則項約為零,對多項式沒有造成任何限制,造成過擬合。只有如中間圖中選取一個適中的 λ {\lambda} λ才可使某些項的權重減小,進行比較合適的曲線擬合。
5.超參數與驗證集
??初學者可能對參數與超參數(hyperparameter)的區別不是很清晰。用多次項擬合例子來說,參數就是指其中每項的權重 w w w的值,合適的 w w w是通過機器學習得到的,而超參數是我們選取用幾次多項式來描述,也可以看做模型容量超參數,另外還有正則項系數 λ {\lambda} λ取什么值,這些通常是人為設定的。有些超參數是無法用訓練集習得的,例如模型容量超參數,如果僅對訓練集來說總會選取更大的模型容量,使得訓練誤差減小,但會造成過擬合,同樣的,對于正則項,僅對訓練集學習會使得正則項為零而使訓練誤差更小,也造成過擬合。
??為了解決這個問題,我們需要一個區別于訓練集的驗證集(validation set)。我們可以將訓練集分成兩部分,一部分對于固定的超參數得到合適的參數w,而另一部分作為驗證集來測試該模型的泛化誤差,然后對超參數進行適宜的調整。簡單概括就是訓練集是為了選取合適的參數,而驗證集是為了選取合適的超參數。
6. 前饋神經網絡
??前饋神經網絡(Deep feedforward network) 可以說是深度學習最核心的模型之一。前饋神經網絡的目的是對于輸入 x x x,假設我們要模擬從輸入到輸出的真實函數 f ? f* f?,神經網絡想要找到這樣的映射 y = f ( x ; θ ) y=f(x;{\theta}) y=f(x;θ)和合適的參數 θ {\theta} θ使得其預測盡量接近真實函數 f ? f* f?。
??其中,前饋代表了所有的信息都從輸入經過某些中間的計算而最終輸出到 ,而不存在從模型的輸出到輸入的反饋(feedback),對于有反饋的情況即為循環神經網絡(recurrent neural network)。前饋網絡已經廣泛應用在工業界,其重要性不言而喻,而且它也是理解在自然語言處理中應用廣泛的循環神經網絡的基礎。
??而網絡則代表了該模型是將不同的基本函數組合在一起形成的模型。例如通過將三個函數 f ( 1 ) f^{(1)} f(1), f ( 2 ) f^{(2)} f(2), f ( 3 ) f^{(3)} f(3)串聯起來構成最終的函數 f ( x ) = f ( 3 ) ( f ( 2 ) ( f ( 1 ) ( x ) ) ) f(x)=f^{(3)}(f^{(2)}(f^{(1)}(x))) f(x)=f(3)(f(2)(f(1)(x))), f ( 1 ) f^{(1)} f(1)就是網絡的第一層, f ( 2 ) f^{(2)} f(2)就是網絡的第二層,以此類推。這個鏈的長度又被稱作網絡的深度(depth),深度學習也因此得名。而前饋網絡的最后一層被稱作輸出層(output layer),對于我們的訓練數據,每一個輸入 x x x都有相應的標記 y = f ? ( x ) y=f^{*}(x) y=f?(x),而網絡的輸出層的結果需要盡量接近 y。但對于其它層來說,和訓練數據沒有這樣的直接對應關系,即我們的算法只要求最后的輸出接近于真實的標記,而對于中間每層的目的并沒有明確定義,所以這些層又被稱作隱藏層(hidden layer)。
??最后,神經代表了它的靈感部分受到了神經科學的影響。每一隱藏層通常是矢量值,而這些隱藏層的維度定義了網絡的寬度。我們可以將每層看做從一個大的從矢量到矢量的函數映射,但從另一方面也可以將矢量的每個元素看做一個小的神經元,每個神經元進行了矢量到標量的映射操作(這一操作又被稱作激活函數,activation function),而每一層是不同的神經元并行運算的綜合。
??前饋神經網絡的提出是為了解決傳統線性模型的一些限制。線性模型如邏輯回歸或者線性回歸的優勢是我們有的可以快速求出解析解,有的可以利用convex optimization來解決。但同時,線性模型也受限于只能模擬線性關系,而很難學習不同輸入參數間的關系。為了將線性模型擴展到非線性函數,我們可以對于輸入 x x x做非線性變換,再利用對于的線性模型解決該問題。
6.1如何選取映射
??選取一個比較通用的 f ? f^{*} f?,例如kernel trick中的RBF kernel(也稱作Gaussian kernel),如果的維度足夠高,我們總能夠使其匹配訓練集,但很難推廣到測試集。因為這種模型只是假設了局域變化不大的前提,而并沒有包含任何有價值的先驗信息。
??人工選取合適的 f ? f^{*} f?,實際上這是在深度學習流行之前普遍采用的方法,但是這需要大量的相關經驗與人力資源,而且不同領域間的知識很難遷移。
??深度學習的策略是利用神經網絡學習合適的用隱藏層代表的映射 f ? f^{*} f?,即模擬 y = f ( x ; θ ; w ) = f ? ( x ; θ ) T w y=f(x;{\theta};w)=f^*(x;{\theta})^Tw y=f(x;θ;w)=f?(x;θ)Tw,其中 θ {\theta} θ是 f ? f^* f?的模擬參數,而 w w w是從 f ? f^* f?到最終輸出的映射參數。它結合了第一和第二種方法,我們可以從比較通用的函數家族中學習 f ? f^* f?,同時也可以利用經驗對函數家族的選擇進行一些限制。與第二種方法比較,其優勢在于我們只需要找到一個比較合適的函數家族,而不需要知道確切的函數。
6.2用神經網絡模擬XOR
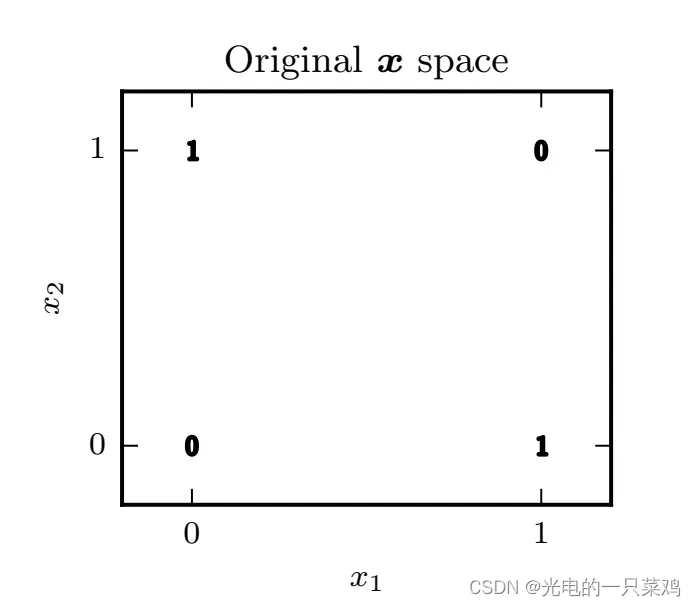
??從圖中可以看出,我們無法對該空間進行線性分割,使得兩個輸出為1的點落在分割線同一側,而兩個輸出為0的點落在分割線另一側。所以,傳統的線性模型無法解決這一問題。為了解決這個問題,我們需要找到一個新的特征空間,使得在新空間中能用線性模型來解決。
??我們引入一個如下圖所示的簡單的具有一層隱藏層的前饋網絡模型:注意圖中兩種方式表示是等價的,左圖是具體畫出每個節點,而右圖是簡化為層。
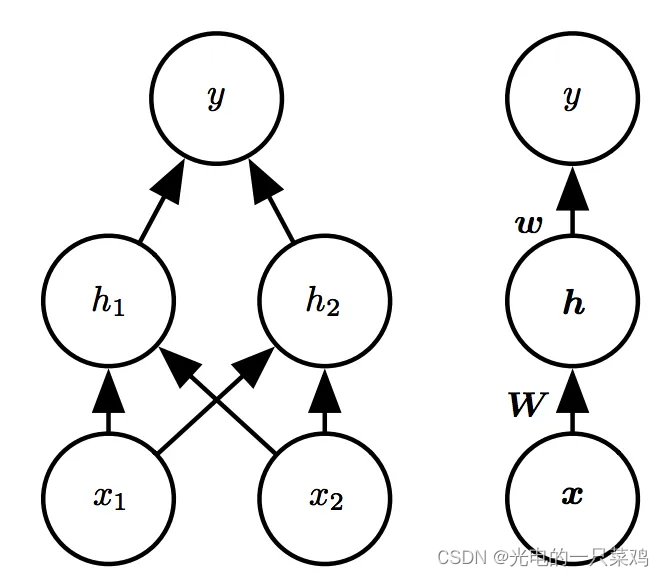
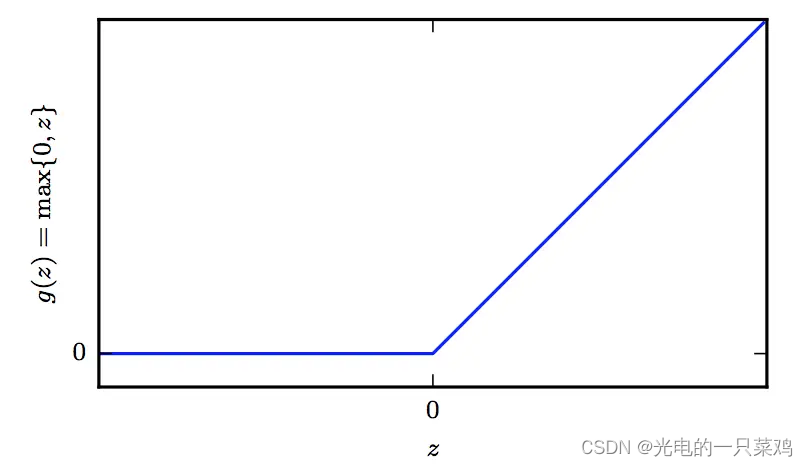
??假設我們用 h = f ( 1 ) ( x ; W ; c ) h=f^{(1)}(x;W;c) h=f(1)(x;W;c)模擬從輸入到到隱藏層的映射,而用 y = f ( 2 ) ( h ; w , b ) y=f^{(2)}(h;w,b) y=f(2)(h;w,b)模擬從隱藏層到輸出的線性映射,則整個模型可以表示為 f ( x ; W , c , w , b ) = f ( 2 ) ( f ( 1 ) ( x ) ) f(x;W,c,w,b)=f^{(2)}(f^{(1)}(x)) f(x;W,c,w,b)=f(2)(f(1)(x)), 那我們如何選取 f ( 1 ) f^{(1)} f(1)呢,通常在神經網絡中我們選稱作rectified linear unit,簡稱為RELU的激活函數,其形式為 g ( z ) = m a x 0 , z g(z)=max{0,z} g(z)=max0,z
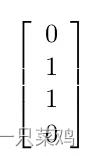
??同時選取 h = f ( 2 ) h=f^{(2)} h=f(2) 為線性函數,我們的模型轉化為 f ( x ; W , c , w , b ) = w T m a x ( 0 , W T x + c ) + b f(x;W,c,w,b)=w^Tmax(0,W^Tx+c)+b f(x;W,c,w,b)=wTmax(0,WTx+c)+b,我們的輸入用矩陣表示為

而希望模擬的對應的輸出是
 對于我們的模型,我們可以找到如下的解
對于我們的模型,我們可以找到如下的解
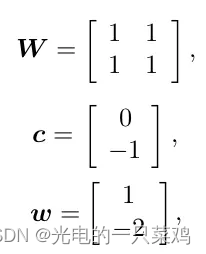
即我們已經從原空間映射到隱藏層所代表的空間
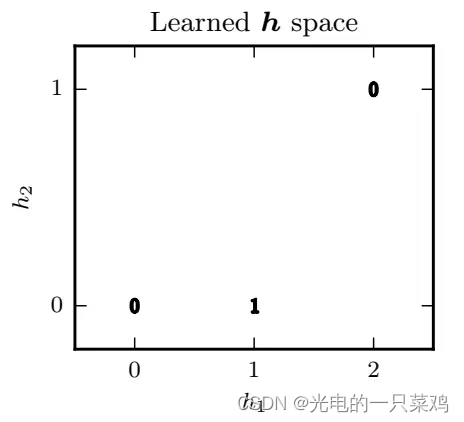
??可以看到在新空間中,原來的輸出為1的兩個點已經匯聚在同一點 h=[1,0]
,因此我們可以找到該空間的線性分割,使得兩個輸出為1的點落在分割線同一側,而兩個輸出為0的點落在分割線另一側。我們繼續將h,w,b代入可得最終輸出
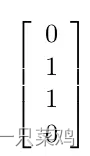
7.損失函數
??神經網絡的設計主要包含兩方面:1)損失函數的選擇 2)模型的具體架構。對于損失函數,我們通常選擇的是減小模型的概率分布與真實的概率分布之間的差異,即交叉熵(cross-entropy):損失函數的具體形式依賴于模型的概率分布
J ( θ ) = ? E x , y p l o g p m o d e l ( y ∣ x ) J({\theta})=-E_{x,y~p}logp_{model}(y|x) J(θ)=?Ex,y?p?logpmodel?(y∣x)
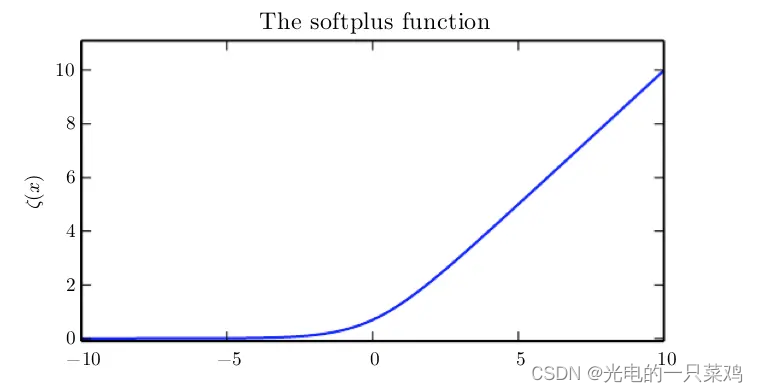
??需要注意的是,由于神經網絡的非線性的特征,我們通常需要用梯度下降的方法逐漸逼近其極值,而且不能保證損失一定會收斂。假如損失函數很容易飽和即在某些區間趨于不變的話,則其梯度很小,梯度下降算法很難更新,所以我們希望損失函數在我們所研究的區間內盡量不飽和。這也是為什么我們通常選取交叉熵的形式,因為很多概率分布函數都會出現指數形式(如sigmoid函數)而在某些區間飽和,交叉熵中的log函數正好可以抵消其飽和,使得模型可以較快更新糾正錯誤預測。
??損失函數的具體形式依賴于神經網絡輸出層的選擇,假設我們的神經網絡已經得到了一系列隱藏特征 h = f ( x ; θ ) h=f(x;{\theta}) h=f(x;θ) ,輸出層就是從隱藏特征向我們的預測目標的映射。對于不同的輸出分布,我們會有不同的輸出函數及損失函數,常見的有如下幾種:
??對于輸出是Bernoulli Distribution的二元分布
??如果我們需要描述目標是多個class的概率分布,我們需要將處理二元分類問題的sigmoid函數擴展,即對于多元分類問題常用的Softmax函數。
對于輸出是高斯分布的情況之前已經總結過,由于線性輸出不存在飽和區間,所以能較好的應用梯度下降算法。
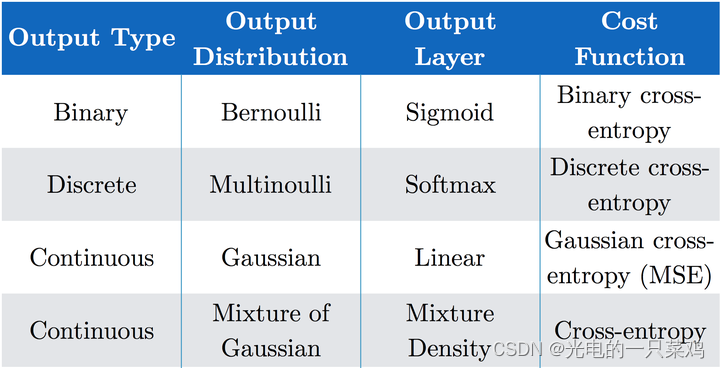
??萬能近似定理證明:僅有一層隱藏層的前饋網絡就足夠表示任何函數的近似到任意的精度,那我們為什么還經常要構建更深層次的網絡呢?原因是如果深度較淺,我們就需要每層有更多的節點即更大的寬度,為達到相同準確度所需要的總節點數更多。另外一方面,淺的網絡也更易過擬合,泛化誤差較大,例如Ian研究了對于圖片地址數字識別的問題,測試準確度會隨著層數的增大而提高:所以通常我們會選取更深的網絡來解決更復雜的問題。總結一下,這部分主要講了神經網絡的損失函數通常用交叉熵,隱藏層通常用ReLU,而更深的模型能有效減少總節點數且減少泛化誤差。
8.反向傳播
??正向傳播就是對于前饋神經網絡來說,信息從輸入到隱藏層再到輸出的正向流動過程,最終會得到損失函數的值。而反向傳播就是從損失函數反向流入網絡以計算梯度(gradient)的過程。要注意,有個普遍的誤解是反向傳播就是神經網絡的全部學習算法,實際上,反向傳播僅指計算梯度的過程,實際上的學習過程是諸如隨機梯度下降(stochastic gradient descent,SGD)更新網絡的算法。
??反向傳播的原理很簡單,就是利用了導數的鏈式法則。我們利用鏈式法則,就可以不斷的從最終的損失函數不斷的反向推導出每層的梯度,而反向傳播就是一種特殊的進行鏈式法則運算的執行過程,即結合了動態規劃(dynammic programming)避免了某些操作的重復性運算,利用較小的存儲代價換取速度的提升。
9.提升模型泛化能力的方法
??總體來說,一部分正則化方法使給模型施加額外的限制條件,例如限制參數值范圍,有些會在目標函數中添加一些額外懲罰項,本質上也是希望限制參數值。有的時候,這些限制條件或懲罰項代表了特定的先驗經驗,有的時候是希望避免模型過于復雜。Parameter Norm Penalties即在目標函數中添加對于參數的懲罰項以減小模型的capacity,
??使機器學習模型效果更好的很自然的一種辦法就是給它提供更多的訓練數據,當然實際操作中,有時候訓練集是有限的,我們可以制造一些假數據并添加入訓練集中,當然這僅對某些機器學習問題適用,例如對于圖像識別,我們可以平移圖像,添加噪聲,旋轉,色調偏移等等,我們希望模型能夠在這些變換或干擾不受影響保持預測的準確性,從而減小泛化誤差。
??與Dataset augmentation類似,多任務學習也是希望令模型的參數能夠進行很好的泛化,其原理是對多個目標共享模型的一部分(輸入及某些中間的表示層),使其對于多個有關聯的目標均有較好的效果,保證模型可以更好的推廣。
??通常對于較大的模型,我們會觀察到訓練集上的誤差不斷減小,但驗證集上的誤差會在某個點之后反而逐漸增大,這意味著為了減小泛化誤差,我們可以在訓練過程中不斷的記錄驗證集上的誤差及對應的模型參數,最終返回驗證集上誤差最小所對應的模型參數,這個簡單直觀的方法就是early stopping,由于其簡單高效,在深度學習中得到了廣泛應用。
??Sparse Representations使參數更稀疏,同樣的我們也可以通過增加對于表征層的norm penalty項使表征(隱藏層)更稀疏。
??Bagging(全稱是bootstrap aggregating)通過整合多個模型來減小泛化誤差,其基本思想是多個模型對于訓練集做出同樣錯誤預測的概率較小,Bagging是ensemble methods(集成算法)的一種方法。
??Dropout可以理解做是將ensemble應用到大型神經網絡的一種更為實際有效的方法。由于ensemble需要訓練多個模型,對于大型神經網絡,其訓練和評估所需時間和存儲資源較大,這種方法常常不太實際,Dropout就提供了一個更便宜的解決方案:即通過隨機去掉一些節點的方法訓練多個子網絡,并最終將這些子網絡ensemble起來。其具體方法是當我們利用minibatch的算法如隨機梯度下降算法來學習時,我們可以隨機的選取一個binary mask(0表示節點輸出為零,1表示正常輸出該節點)決定哪些輸入和隱藏層節點保留,每次的mask的選擇是獨立的。而mask為1的概率是我們可以調控的超參數。和bagging方法相比,bagging中每個模型是完全獨立的,而dropout中,模型間由于繼承了父網絡中的參數的子集會共享一些參數,這使得在有限的存儲空間中我們可以表示多個模型。以上是訓練過程,而在做inference預測時,我們需要取所有模型的預測的均值,但是這往往計算量過多,Hinton提出inference時我們實際可以只用一個模型但其中每個節點的權重需要乘以包含這個節點的概率,這種方法稱作weight scaling inference rule。實際中,我們常常把weight scaling過程放在訓練過程中,即訓練中每個節點輸出就乘以包含該節點的概率的倒數,則inference時只需要正常的通過一遍前饋過程即可,不需要在進行weight scaling。Dropout的優勢在于其計算資源占用小,并且對于模型或訓練算法的限制較小,基本上可以適用于各種前饋網絡,循環網絡或概率模型,所以實際工業模型中應用很多。
??Adversarial Training對抗訓練很有意思,它讓人們深入思考機器學習究竟學到了什么有效信息。這方面的工作主要是由谷歌的Szegedy和本書作者Ian Goodfellow進行的。他們可以制造一些對抗樣本迷惑神經網絡,如下圖中所示,他們對于熊貓圖片加了一些人眼不可見的干擾,形成新樣本,而新的人眼仍可鑒定為熊貓的圖片卻會被機器以較大置信率鑒定為長臂猿。

??為什么在人類看來類似的樣本機器會得到大相徑庭的結論呢?Ian認為這是由于神經網絡中的大部分組成還是線性的(如ReLU可以看成是分段線性),而對于不同的輸入,線性函數會受到較大的擾動,產生較大的改變。為了解決這一問題,他們會將這些對抗樣本重新加到訓練集中,使得神經網絡傾向于對于數據集保持局部穩定而不至干擾過大,從而學習到更有效的信息。
10.優化方法歸納
??隨著樣本的增多,計算梯度的準確度的回報是小于線性的。例如我們有兩種方法:1. 利用100個樣本計算梯度 2.利用10000個樣本計算梯度。 第二種方法是第一種的100倍的計算量,但只將均值的標準差減少了10倍,我們通常希望我們能更快的達到我們的優化目標,所以不需要每次計算梯度都嚴格的利用全部樣本,而是進行多次iteration,而每次估算的梯度有合適的準確度即可。在優化算法里,我們通常把一次僅利用一個樣本來更新的方式叫做stochastic或online 方法。但對于深度學習來講,我們通常所說的stochastic gradient descent指的是minibatch stochastic methods,即每次計算梯度時利用一部分樣本,其樣本量是新引入的超參數batch size。注意到,我們引入了另一個超參數學習率 ,可以說學習率是深度學習中最重要的需要調節的參數,如果學習率過大,我們可能會一次就跳過極小點而到山谷的另一側,那么訓練的loss可能會有較大波動而不是一致的向極小點步進,另一方面,如果學習率過小,訓練更新過小,需要較長時間才能達到較好效果。通常我們需要經過不斷的試驗來選取合適的學習率,另外也可以在初始時使用稍大一些的學習率,隨著訓練的進行我們可以逐步的降低學習率從而避免波動,而之后保持學習率恒定。
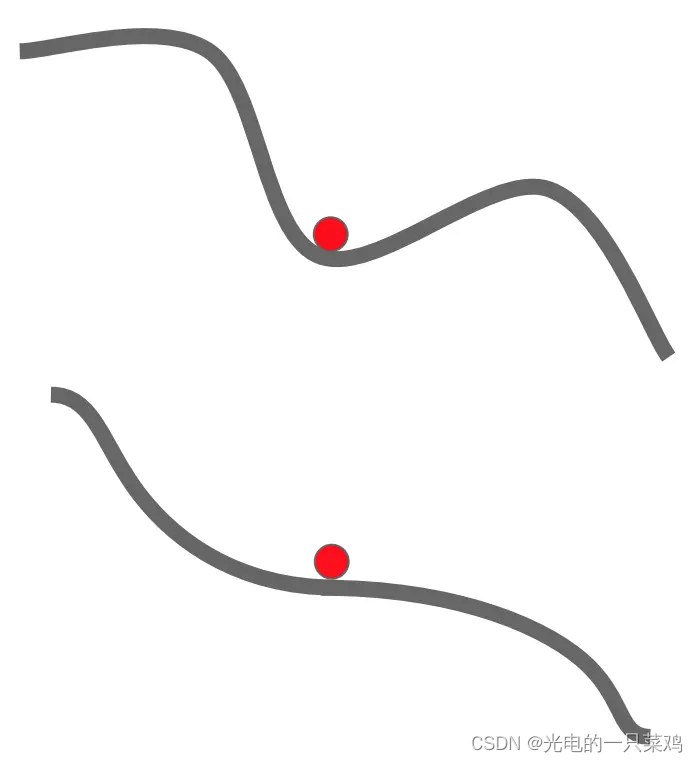
??Momentum,顧名思義,來自物理學中的動量概念,即我們用一個新的變量(可以看做是速度,在質量為單位質量時大小等于Momentum)來記錄之前的梯度變化的速度,其優勢在于對于局域極小值或鞍點的情況,由于保持了原有的速度,模型可以繼續更新。
??而對于不同方向的曲率不同的問題,由于其保持一定原有方向的速度,不會在曲率較大的山峰間進行劇烈波動,如下圖藍線所示:
??AdaGrad沒有引入速度變量 ,而是記錄每個參數方向上的梯度的值的平方和,在該參數方向上步進時除以這個平方和的平方根,則對于原梯度較小學習進展較慢的方向相較于原梯度較大的方向rescale的程度較小,從而加速在該方向上的學習進程。Adagrad雖然可以較好的解決不同方向曲率差異過大的情況,但是我們可以看到隨著訓練的進行,習率衰減依賴于所有之前的梯度的歷史結果,可能在我們未達到極值點前學習率已經減至過低從而無法有效的更新模型。所以RMSProp方法在其上做了改進,計算的是一個帶有指數權重的moving average。
Adam 可以看做是RMSProp 與Momentum方法的一種結合,其得名于Adaptive moments,意在結合兩者的優點。它引入兩個moment, 第一個即為速度的Momentum,第二個moment則是如RMSProp中的梯度的平方和,并分別對兩個moment進行一些隨時間變化的修正。實際應用中,選擇Adam和合適的參數能夠適用于大部分深度學習優化問題。
11.卷積神經網絡
??繼續深度學習花書的讀書筆記總結,這一章主要介紹了卷積神經網絡(convolutional neural network, 簡稱CNN), 它通常適用于具有網格狀結構的數據,例如時序數據可看做是在特定時間間隔上的一維網格,圖像可以看做是像素構成的二維網格,醫學成像如CT等為三維網格數據。
??卷積神經網絡,顧名思義,利用了數學上的卷積操作(convolution)。和前面總結的基本的前饋神經網絡相比,CNN只不過是將某層或某幾層中的矩陣乘法運算替換為卷積運算,其他的比如說最大似然法則,反向傳播算法等等都保持不變。
??對于傳統的神經網絡來說,由于其操作是矩陣乘法,每一個輸入與輸出元之間都需要一個獨立的參數來表示,這代表每個輸出元與每個輸入元之間都有連接,我們就需要很大的空間來存儲這些參數,而對于CNN來說,通常其kernel的大小遠小于其輸入的大小,例如對于圖像數據,輸入常常有成千上萬的像素,而對于檢測圖像中邊的結構的kernel可能只需要利用十至百個像素即可,這極大的減小了存儲所需空間,而且減小了計算輸出時的計算量。對于m個輸入和n個輸出,矩陣乘法需要 個參數,其運算時間為 ,而假如我們限制每個輸入到輸出的連接為k個,則我們僅需要 個參數,且運算時間為 。如圖中所示,上圖為卷積操作,下圖為矩陣乘法,可見卷積操作總的連接數大大減小.
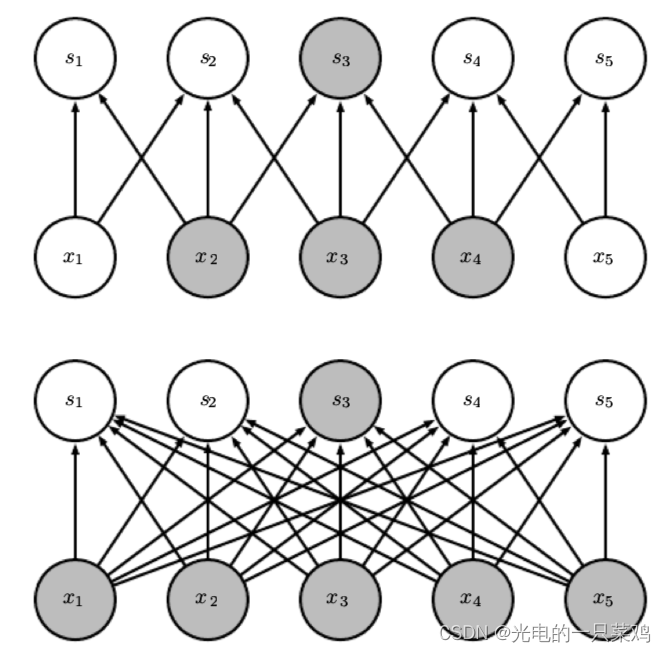
??另外,對于傳統神經網絡來說,每一個輸入至輸出的元素都是獨立的,只對于輸入的一個元素起作用,而對于CNN來說,kernel的矩陣元素對于輸入的每一個元素都起作用,實現了參數的共享,如圖中所示,上圖是一個kernel大小為3的卷積神經網絡,其中深黑色箭頭代表的kernel中間的元素對于每一個 到 的運算都起作用,而對于下圖矩陣乘法來講,黑色箭頭代表的權重矩陣中的元素僅對 到 的運算起作用。
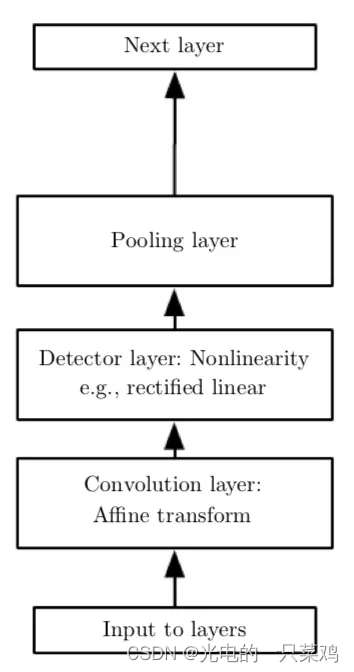
??除了卷積層之外,CNN中還有常用的操作是pooling function,其作用是利用附近元素的統計信息來代替其原有的值,其目的是可以使結果在對于輸入的小量改變的干擾下保持穩定。例如,一個經典的pooling function是max pooling,即將周圍小方格中的最大值作為輸出值,當某一輸入值改變時,對最大值影響較小,保持了輸出的穩定。加入pooling后,卷積的基本單元包括卷積層(convolution layer),激活函數的非線性Detector layer,以及pooling layer
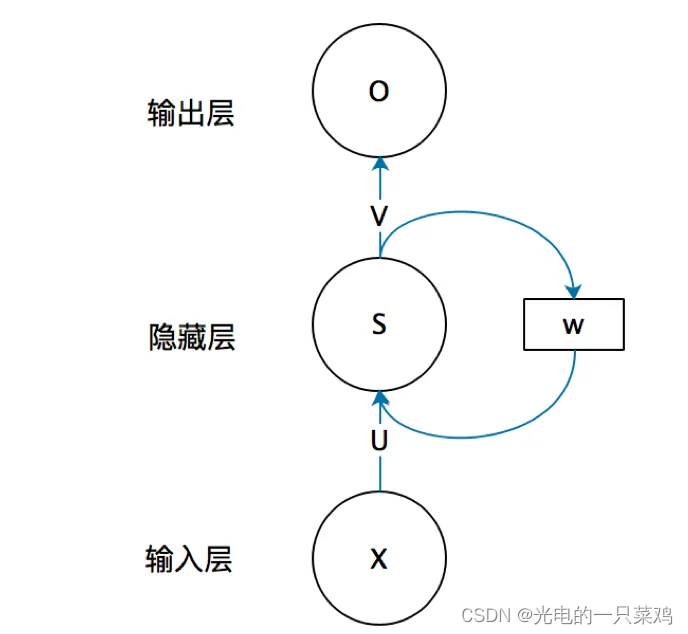
12.循環神經網絡
??循環神經網絡(Recurrent neural network, 簡稱RNN),主要用來處理序列數據,比如一些文字序列或時序數據。對于這類數據,基本的前饋神經網絡會對每一個輸入的特征都訓練一個單獨的參數,而不能很好的進行參數的共享,而RNN就可以通過對不同時間點的特征共享參數而更容易的進行訓練,泛化效果也更好。RNN與CNN不同的地方在于其每一點的輸出還依賴于之前的結果。
13.對抗神經網絡
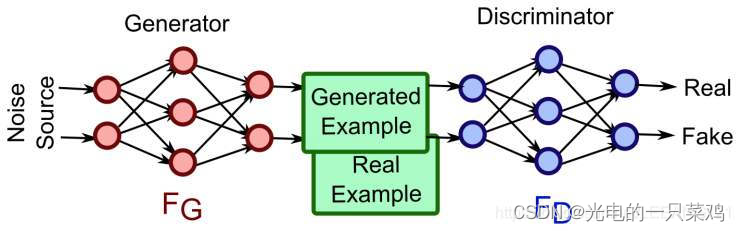
??GAN的全稱是Generative adversarial network,中文翻譯過來就是對抗式神經網絡。對抗神經網絡其實是兩個網絡的組合,可以理解為一個網絡生成模擬數據(生成網絡Generator),另一個網絡判斷生成的數據是真實的還是模擬的(判別網絡Discriminator)。生成網絡要不斷優化自己生成的數據讓判別網絡判斷不出來,判別網絡也要優化自己讓自己判斷得更準確。二者關系形成對抗,因此叫對抗神經網絡。
??GAN網絡最強大的地方就是可以幫助我們建立模型,而不像傳統的網絡那樣是在已有模型上幫我們更新參數而已。同時,GAN網絡是一種無監督的學習方式,它的泛化性非常好。


—— 筑夢之路)





)


短訓練序列:STS(含Matlab和verilog代碼))

)


)


)