目錄

一.求鏈式二叉樹節點個數

二.求鏈式二叉樹葉子節點個數

?三.求鏈式二叉樹第k層節點個數

?四.求鏈式二叉樹的深度/高度

?五.鏈式二叉樹查找值為x的節點

?六.鏈式二叉樹的銷毀?

七. 測試函數

八. 總結:

---

前言:

在學習鏈式二叉樹的常用操作之前 我們需要手動創建一個二叉樹 在上文的學習中 我們已經學習過了 鏈式二叉樹的創建 代碼如下

#define _CRT_SECURE_NO_WARNINGS 
#include <stdio.h>
#include <stdlib.h>
#include <assert.h>// 二叉樹節點結構定義
typedef char BTDataType;
typedef struct BinaryTreeNode {BTDataType data;struct BinaryTreeNode* left;struct BinaryTreeNode* right;
} BTNode;// 創建新節點
BTNode* BuyBTNode(BTDataType x) {BTNode* node = (BTNode*)malloc(sizeof(BTNode));if (node == NULL) {printf("malloc failed\n");exit(-1);}node->data = x;node->left = NULL;node->right = NULL;return node;
}// 構建示例二叉樹（便于測試）
BTNode* CreateBinaryTree() {BTNode* nodeA = BuyBTNode('A');BTNode* nodeB = BuyBTNode('B');BTNode* nodeC = BuyBTNode('C');BTNode* nodeD = BuyBTNode('D');BTNode* nodeE = BuyBTNode('E');BTNode* nodeF = BuyBTNode('F');nodeA->left = nodeB;nodeA->right = nodeC;nodeB->left = nodeD;nodeC->right = nodeE;nodeC->left = nodeF;return nodeA;
}

一.求鏈式二叉樹節點個數

代碼實現：?

// 一、求二叉樹節點個數
int BinaryTreeSize(BTNode* root) {// 空樹節點個數為0return root == NULL ? 0 : 1 + BinaryTreeSize(root->left) + BinaryTreeSize(root->right);
}

• 功能：計算二叉樹中所有節點的總數。
• 實現思路：
  • 空樹（root == NULL）返回 0；
  • 非空樹則返回「1（當前節點）+ 左子樹節點數 + 右子樹節點數」；
  • 遞歸遍歷整個樹，累加所有節點。
• 時間復雜度：O (n)，需訪問每個節點一次。

二.求鏈式二叉樹葉子節點個數

代碼實現：

// 二、求二叉樹葉子節點個數
int BinaryTreeLeafSize(BTNode* root) {// 空樹葉子節點個數為0if (root == NULL) {return 0;}// 左右孩子都為空的節點是葉子節點if (root->left == NULL && root->right == NULL) {return 1;}// 遞歸計算左右子樹的葉子節點總和return BinaryTreeLeafSize(root->left) + BinaryTreeLeafSize(root->right);
}

• 功能：統計二叉樹中葉子節點（無左右子樹的節點）的數量。
• 實現思路：
  • 空樹返回 0；
  • 若當前節點的左右指針均為NULL，則是葉子節點，返回 1；
  • 否則遞歸計算左子樹和右子樹的葉子節點之和。

?三.求鏈式二叉樹第k層節點個數

代碼實現：?

// 三、求二叉樹第k層節點個數
int BinaryTreeLevelKSize(BTNode* root, int k) {assert(k >= 1); // k必須是正整數// 空樹或k小于1，返回0if (root == NULL) {return 0;}// 第1層只有根節點if (k == 1) {return 1;}// 第k層節點個數 = 左子樹第k-1層節點數 + 右子樹第k-1層節點數return BinaryTreeLevelKSize(root->left, k - 1) + BinaryTreeLevelKSize(root->right, k - 1);
}

• 功能：計算二叉樹中第 k 層（根節點為第 1 層）的節點總數。
• 實現思路：
  • 邊界檢查：k < 1時斷言報錯，空樹返回 0；
  • 遞歸降層：第 k 層節點數等價于左右子樹第 k-1 層節點數之和；
  • 終止條件：k == 1時，當前節點即為第 1 層節點，返回 1。
• 注意：若 k 大于樹的深度，返回 0。

?四.求鏈式二叉樹的深度/高度

?代碼實現：

// 四、求二叉樹的深度/高度
int BinaryTreeDepth(BTNode* root) {// 空樹深度為0if (root == NULL) {return 0;}// 計算左右子樹深度int leftDepth = BinaryTreeDepth(root->left);int rightDepth = BinaryTreeDepth(root->right);// 樹的深度 = 左右子樹最大深度 + 1（當前節點）return leftDepth > rightDepth ? leftDepth + 1 : rightDepth + 1;
}

• 功能：計算二叉樹的最大深度（從根節點到最遠葉子節點的層數）。
• 實現思路：
  • 空樹深度為 0；
  • 遞歸計算左子樹和右子樹的深度；
  • 當前樹的深度 = 左右子樹中最大深度 + 1（當前節點所在層）。
• 特點：體現了「分治思想」，將樹的深度問題分解為子樹的深度問題。

?五.鏈式二叉樹查找值為x的節點

代碼實現：

// 五、二叉樹查找值為x的節點
BTNode* BinaryTreeFind(BTNode* root, BTDataType x) {// 空樹返回NULLif (root == NULL) {return NULL;}// 找到目標節點，返回該節點指針if (root->data == x) {return root;}// 先在左子樹查找BTNode* leftRet = BinaryTreeFind(root->left, x);if (leftRet != NULL) {return leftRet;}// 左子樹沒找到，再在右子樹查找BTNode* rightRet = BinaryTreeFind(root->right, x);return rightRet;
}

• 功能：在二叉樹中查找值為 x 的節點，返回該節點的指針（若不存在返回NULL）。
• 實現思路：
  • 空樹返回NULL；
  • 先檢查當前節點是否為目標節點，是則返回；
  • 否則先遞歸查找左子樹，找到則返回；
  • 左子樹未找到時，遞歸查找右子樹并返回結果。
• 查找順序：本質是「前序遍歷查找」，先根節點，再左子樹，最后右子樹。

?六.鏈式二叉樹的銷毀?

代碼實現:

// 六、二叉樹的銷毀
void BinaryTreeDestroy(BTNode** root) {// 空樹直接返回if (*root == NULL) {return;}// 先銷毀左子樹BinaryTreeDestroy(&(*root)->left);// 再銷毀右子樹BinaryTreeDestroy(&(*root)->right);// 最后釋放當前節點free(*root);*root = NULL; // 避免野指針
}

• 功能：釋放二叉樹所有節點的內存，徹底銷毀樹結構。
• 實現思路：
  • 采用「后序遍歷」思路：先銷毀左子樹，再銷毀右子樹，最后釋放當前節點；
  • 使用二級指針**root，確保銷毀后根節點被置為NULL，避免野指針；
  • 遞歸釋放所有節點，無內存泄漏。
• 關鍵：必須先釋放子樹，再釋放當前節點，否則會丟失子樹指針導致內存泄漏。

七. 測試函數

//測試函數
int main() {BTNode* root = CreateBinaryTree();// 測試節點個數printf("二叉樹節點總數: %d\n", BinaryTreeSize(root));// 測試葉子節點個數printf("二叉樹葉子節點個數: %d\n", BinaryTreeLeafSize(root));// 測試第k層節點個數printf("第2層節點個數: %d\n", BinaryTreeLevelKSize(root, 2));printf("第3層節點個數: %d\n", BinaryTreeLevelKSize(root, 3));// 測試樹的深度printf("二叉樹深度: %d\n", BinaryTreeDepth(root));// 測試查找節點BTNode* findNode = BinaryTreeFind(root, 'E');if (findNode != NULL) {printf("找到節點: %c\n", findNode->data);}else {printf("未找到節點\n");}// 銷毀二叉樹BinaryTreeDestroy(&root);assert(root == NULL); // 驗證樹已被銷毀return 0;
}

代碼運行結果如下:

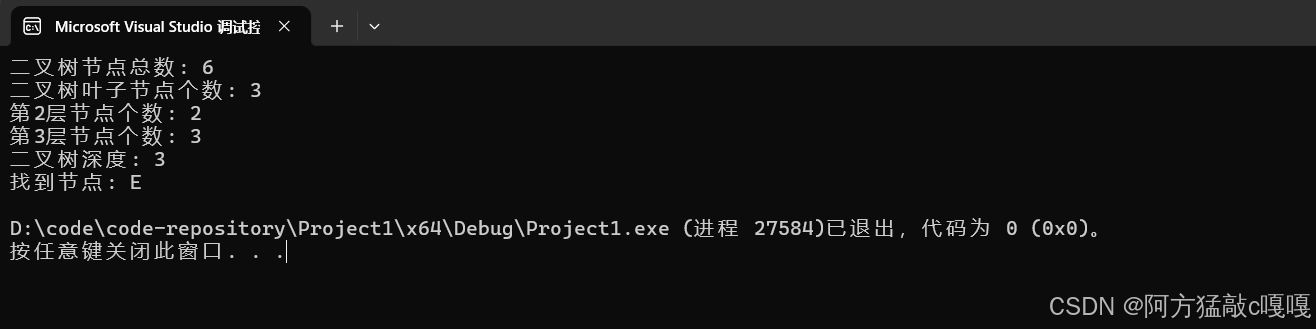
鏈式二叉樹如下圖 進行驗證

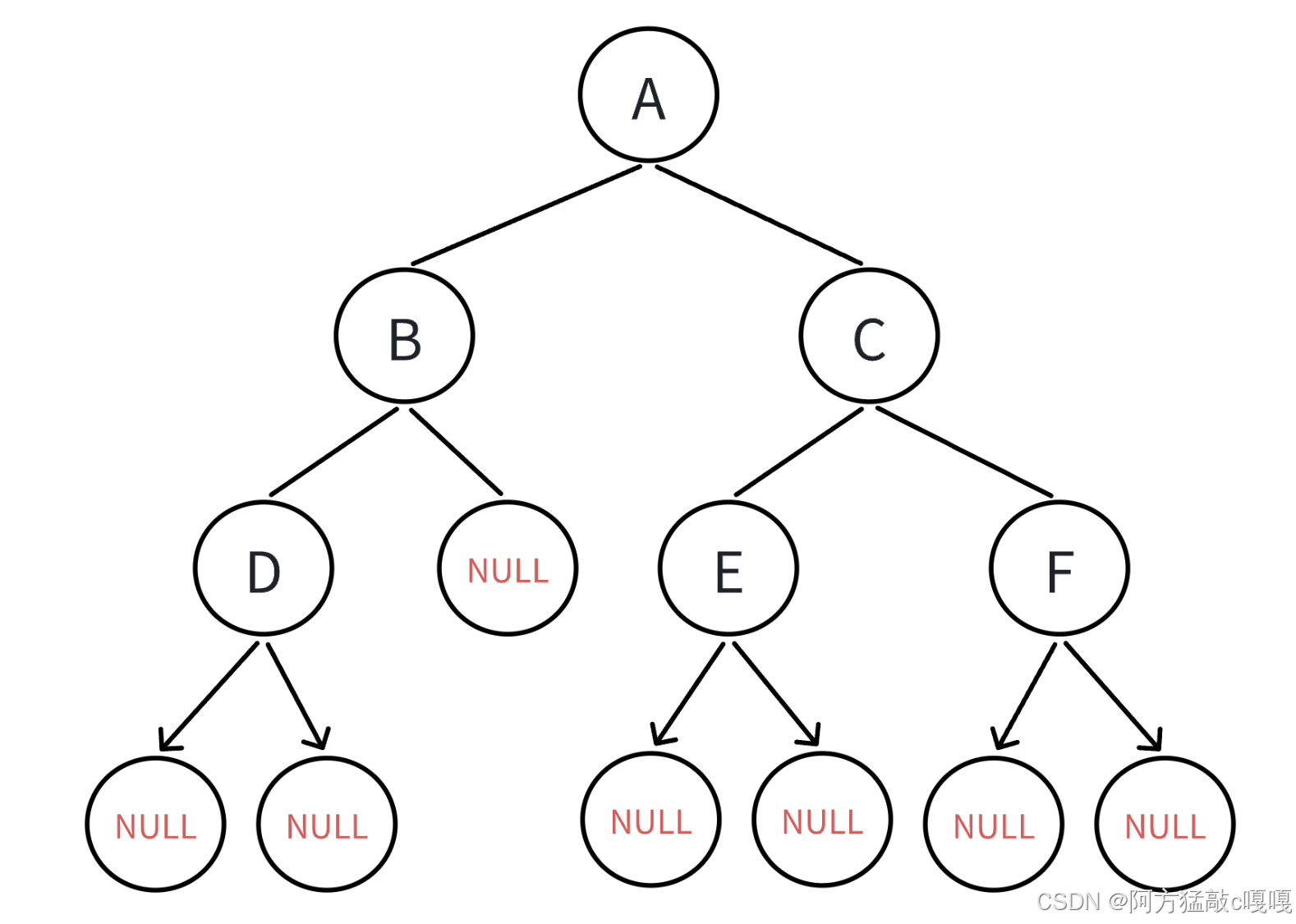
根據上圖 不難得出 代碼運行 正確

八. 總結:

所有函數均采用遞歸實現，符合二叉樹的遞歸特性（每個節點的左、右子樹仍是二叉樹）。核心思想是「分治」：將對整棵樹的操作分解為對根節點和左右子樹的操作，簡化問題復雜度。每個函數的時間復雜度均為 O (n)（n 為節點總數），空間復雜度為 O (h)（h 為樹的高度，遞歸棧的深度）。