1. 背景介紹

之前已經介紹過“無模型預測控制（Model-Free Predictive Control/MFPC）”中的“無模型預測電流控制（Model-Free Predictive Current Control/MFPCC）”，可參考下面知乎。

https://zhuanlan.zhihu.com/p/660705382https://zhuanlan.zhihu.com/p/660705382

但是后來也有說過，這個MFPCC，其實是利用擴張狀態觀測器（Extended State Observer/ESO）消除了磁鏈和電阻的影響。電感則是影響了MFPCC的增益，如果增益設置的不恰當，MFPCC依舊會性能不佳，甚至失去穩定。

今年在預測控制大會上聽了汪老師的報告，其報告內容就屬于下面這篇參考文獻。

[1] F. Wang, Y. Wei, J. Rodriguez and C. Garcia, "State-of-Art, Development, and Challenges of Model-Free Predictive Control on Motor Drives," in IEEE Transactions on Power Electronics, vol. 40, no. 8, pp. 10846-10864, Aug. 2025, doi: 10.1109/TPEL.2025.3559514.

論文中有下面一張圖，我覺得畫的很形象。圖中的MBPC為model-based predictive control，即“基于模型的預測控制”。圖中的Data-driven就是“adj. 數據驅動的”，關于“數據驅動”，官方化的解釋為：數據驅動的概念由全國科學技術名詞審定委員會于2008年審定發布，其核心內涵是以數據為核心驅動力，通過數據采集、清洗、建模和分析提取價值信息，支撐高效決策與操作的技術范式。

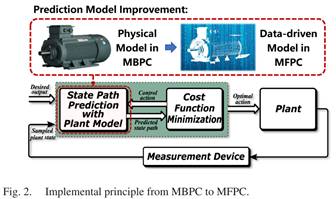
我個人的拙見：“數據驅動”放在電機控制系統而言，相當于根據電機運行得到的電流（包括電流變化量）以及參考電壓數據（包括電壓變化量），并利用一些算法得到這些之間內在聯系，進而擬合出一個“虛構的電機模型”，并根據這個“虛構的電機模型”對電機實行控制。

根據汪老師的報告，我找到了其在24年發表的TIE，以這篇文獻為基礎來學習一下Data-driven Model in MFPC。

論文鏈接：https://ieeexplore.ieee.org/document/10505794

[2] Y. Wei, H. Young, D. Ke, F. Wang, H. Qi and J. Rodríguez, "Model-Free Predictive Control Using Sinusoidal Generalized Universal Model for PMSM Drives," in IEEE Transactions on Industrial Electronics, vol. 71, no. 11, pp. 13720-13731, Nov. 2024, doi: 10.1109/TIE.2024.3379667.

文章的摘要：“為了解決模型預測控制(MPC)中參數失配導致的魯棒性較差的問題，無模型預測控制在電機驅動系統中得到了廣泛的應用。該方法用數據驅動模型代替先驗模型，消除了物理參數的影響。然而，旋轉坐標系對模型精度的影響是多方面的，特別是位置信號不準確和控制器不對稱會造成誤差。本文提出了一種無模型預測控制策略，利用正弦廣義通用模型直接控制正弦信號，并結合歷史數據提高了模型精度，反映了被控對象的運動特性。該模型是根據被控對象的信號變化設計的，并使用遞推最小二乘(RLS)算法在線估計系數以確保模型的精度。為了在連續控制集(CCS)控制器中實現控制，利用時移和拉格朗日算法設計了預測信號，并根據極點/零點位置和微分方程組分析了預測信號的基本性能和穩定性。將該控制策略作為預測電流控制策略應用于永磁同步電機(PMSM)驅動系統，給出了不同運行條件下的實驗結果，驗證了該方法的有效性和優越性。”

2. 算法的簡單介紹

所提算法的控制框圖如下。其采用雙閉環控制，外環采用傳統的PI控制，速度外環產生的參考電流經過坐標變換后得到阿爾法α，貝塔β電流的參考值。然后內環采用所提的基于“數據驅動”的無模型預測電流控制。

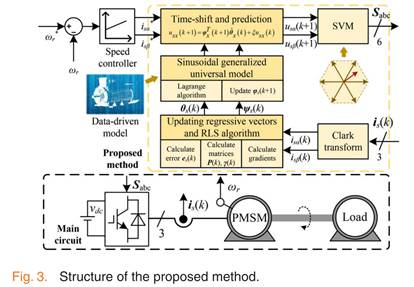
其電流環的算法框圖如下：

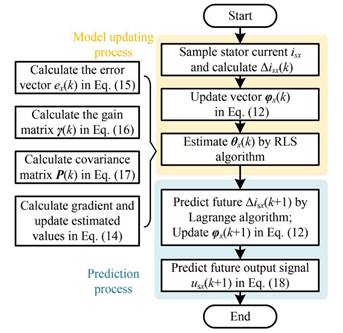
下面我們來詳細看看相關公式。首先是式子(9)-(11)。

式子(9)的意思是，電機系統的k+1時刻的電壓增量，可以通過往期的n+1組電流增量數據以及m+1組電壓增量數據得到（在文中，這個n，m取2或者3即可）。

那接下來的問題就是，這n+1組電流增量數據以及m+1組電壓增量數據與k+1時刻的電壓增量的關系，到底從何而來？這時候就需要看到式子(12)到式子(18)。

文中中是用“最小二乘法”去擬合n+1組電流增量數據以及m+1組電壓增量數據與k+1時刻的電壓增量的關系。當然你換別的方法也可以。

這里值得注意的一些問題是，k+1時刻的參考電流到底從何而來？文章說采用拉格朗日算法，但文章沒給具體的公式。我是在汪老師的另一篇論文找到了相關公式。公式如下：

[3] F. Wang, Y. Wei, H. Young, D. Ke, D. Huang and J. Rodríguez, "Continuous-Control-Set Model-Free Predictive Control Using Time-Series Subspace for PMSM Drives," in IEEE Transactions on Industrial Electronics, vol. 71, no. 7, pp. 6656-6666, July 2024, doi: 10.1109/TIE.2023.3310017.

我自己在仿真中的話，是利用dq電流的參考電流，經過坐標變換得到k+1時刻的參考電流。

值得注意的是，論文中的(14)-(17)所寫出的最小二乘法表達式略有所錯誤(個別字母/符號標錯)，需要自己重新推導且去了解其這樣設計的含義。這點小差錯不影響文章的思路。

該算法是在線運行的，并不是離線驅動。需要電機先跑起來一下，便可以切換到該基于“數據驅動”的無模型預測電流控制。

下面先進行仿真驗證，在本文的第三節驗證模型數據的數量選擇的影響以及反饋系數的影響。第四節進行算法對比。

3.參數影響

仿真參數設置：

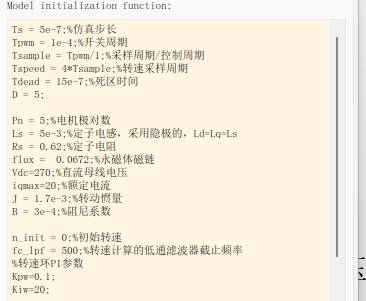
仿真工況設置：

0.4s前，電流環采用傳統的電流環控制方式，電機給定轉速為2000r/min，負載為8Nm；前0.4s相當于為數據驅動無模型預測電流控制提供必要的“數據”信息。0.4s之后切入數據驅動無模型預測電流控制，并且在0.6s處讓電機減速1000r/min，在0.8s減載至5Nm，以驗證電機的動態性能。

3.1 數據量選擇的影響

文中說需要n+1組電流增量數據以及m+1組電壓增量數據去計算k+1時刻的電壓增量。文中說，n和m取2或者3即可。

在汪老師的另一篇文獻中做了自適應的階數選擇，其實驗結果也是在2、3之間波動。

[4] Y. Wei, H. Young, D. Ke, D. Huang, F. Wang and J. Rodríguez, "Adaptive Ultralocalized Time-Series for Improved Model-Free Predictive Current Control on PMSM Drives," in IEEE Transactions on Power Electronics, vol. 39, no. 5, pp. 5155-5165, May 2024, doi: 10.1109/TPEL.2024.3357854.

3.1.1 n = m = 2的仿真波形

n = m = 2，即采用3組電流增量數據以及3組電壓增量數據去擬合k+1時刻的電壓，仿真的整體波形如下。

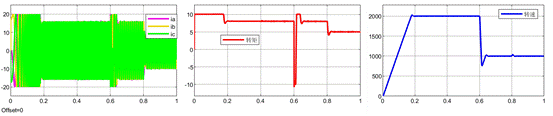
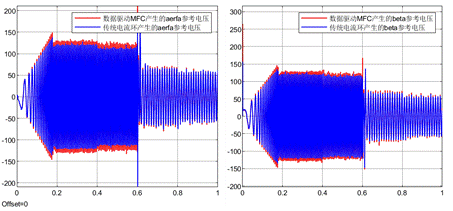
下面是傳統電流環和數據驅動無模型預測電流控制產生的阿爾法貝塔參考電壓的對比。從下面的波形可以看到，兩種算法產生的參考電壓差不多，有一定偏差。兩種算法產生的參考電壓差不多說明二者性能也將差不多。

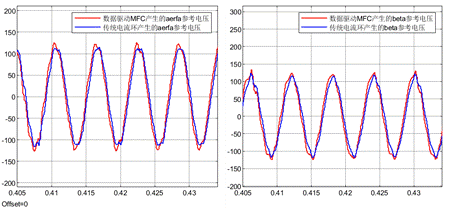
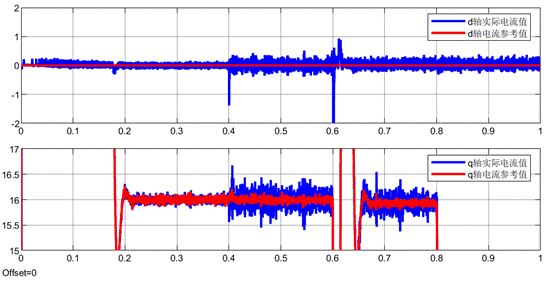
下面放大dq電流波形，可以看到，其實在0.4s切換到數據驅動無模型預測電流控制，是會出現更大的電流波動。但是考慮到該算法畢竟不需要任何的電機參數，其還是有明顯的價值的。

3.1.2 n = m = 3的仿真波形

n = m = 3，即采用4組電流增量數據以及4組電壓增量數據去擬合k+1時刻的電壓，仿真的整體波形如下。

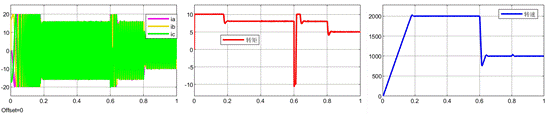
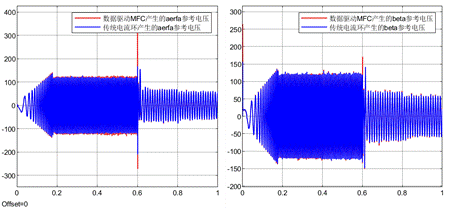
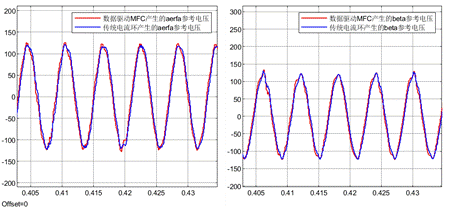
下面是傳統電流環和數據驅動無模型預測電流控制產生的阿爾法貝塔參考電壓的對比。從下面的波形可以看到，兩種算法產生的參考電壓基本一致，這說明：

（1）對該仿真條件而言，相比于3組電流增量數據以及3組電壓增量數據（n = m = 2），采用4組電流增量數據以及4組電壓增量數據（n = m = 3）能夠實現更好的擬合擬合效果。

（2）該數據驅動無模型預測電流控制可以在不需要任何電機參數的條件下就可以實現與傳統算法基本一致的性能。

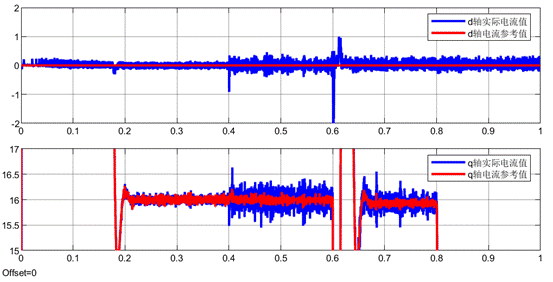
下面放大dq電流波形，可以看到，其實在0.4s切換到數據驅動無模型預測電流控制，是會出現更大的電流波動。但是考慮到該算法畢竟不需要任何的電機參數，其還是有明顯的價值的。

3.2 反饋增益的影響

論文中的控制律涉及到一個反饋系數。

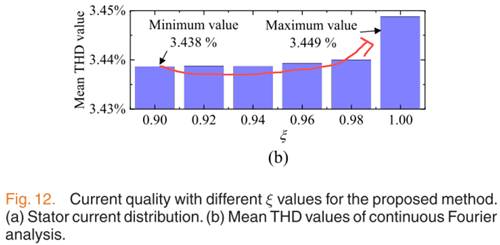
從圖12的實驗結果可以看到，當反饋系數在0.90到1之間時，總的來說，電流THD會隨著反饋系數的提高而增加。

下面就進行了不同反饋系數的仿真對比，反饋系數分別取0.9和1.0。從下面仿真可以看到，反饋系數為0.9時的相電流THD（1.16%）確實會略低于反饋系數為1時的相電流THD（1.32%），這與實驗的情況基本一致。

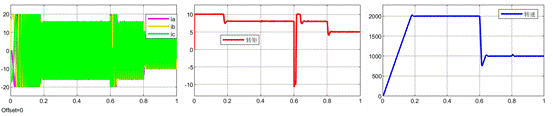
反饋系數為0.9的整體波形

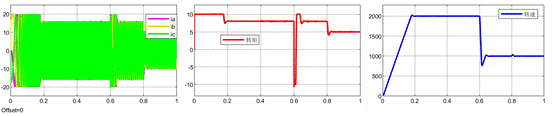
反饋系數為1的整體波形

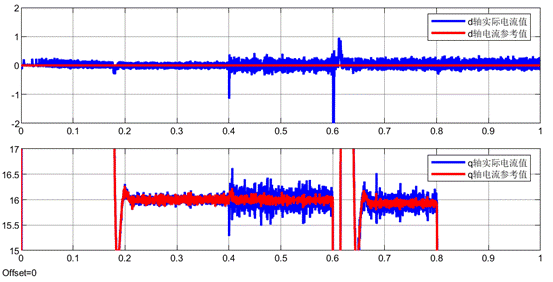
反饋系數為0.9的dq電流波形

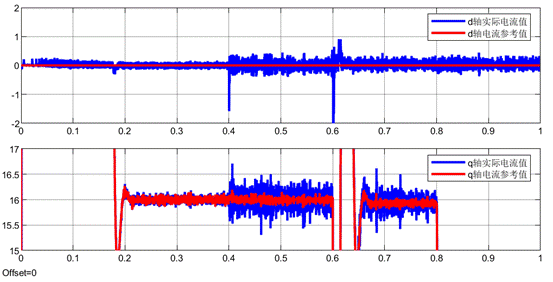
反饋系數為1的dq電流波形

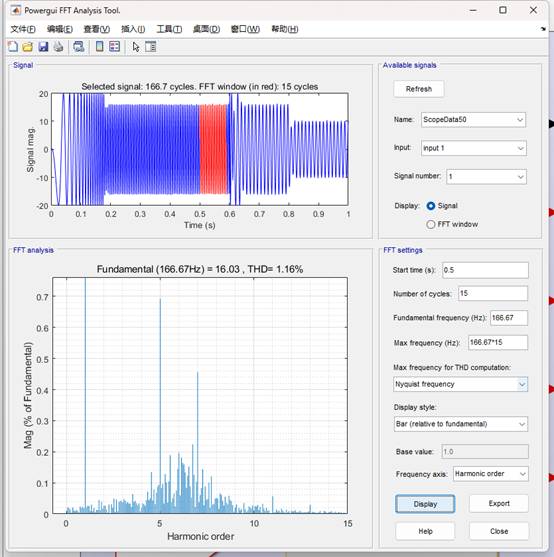
反饋系數為0.9的相電流FFT分析

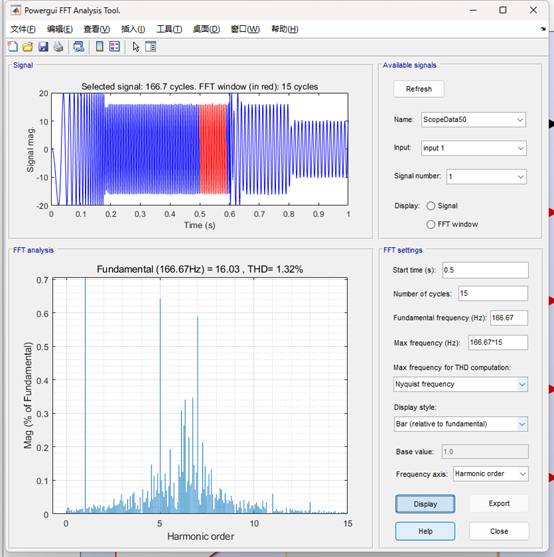
反饋系數為1的相電流FFT分析

4. 仿真對比

下面進行三組仿真的對比：

1. 基于LESO的MFPCC（LESO的帶寬取為4000，控制器中的電感參數設置為實際電感參數）

2. 基于數據驅動的MFPCC（n=m=3，反饋系數取0.9）

3. 基于LESO的MFPCC（LESO的帶寬取為4000，控制器中的電感參數設置為實際電感參數的2倍，以模擬參數失配）

PS：對于基于數據驅動的MFPCC，在0.3s前，由基于LESO的MFPCC驅動電機，以其數據作為基于數據驅動的MFPCC的支撐。0.3s后切入基于數據驅動的MFPCC。

4.1 整體波形的對比

下面是整體波形的對比。從下面仿真可以得到以下結論。

（1）對于基于LESO的MFPCC，在控制器中的電感參數設置為實際電感參數時，其控制效果極佳；

（2）但當控制器中的電感參數設置為實際電感參數的2倍時，系統開始引入大量高頻噪聲；

（3）相對基于LESO的MFPCC（控制器中的電感參數設置為實際電感參數），基于數據驅動的MFPCC的轉矩脈動有所增加。

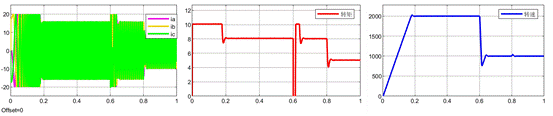
基于LESO的MFPCC（控制器中的電感參數設置為實際電感參數）

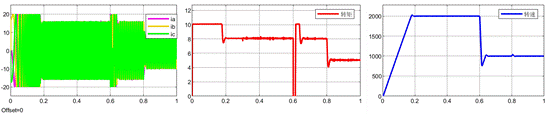
基于數據驅動的MFPCC

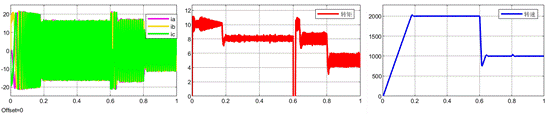
基于LESO的MFPCC（控制器中的電感參數設置為實際電感參數的2倍）

4.2 相電流FFT的對比

（1）基于LESO的MFPCC（控制器中的電感參數設置為實際電感參數）的電流THD為0.55%；

（2）基于數據驅動的MFPCC的電流THD為1.13%

（3）基于LESO的MFPCC（控制器中的電感參數設置為實際電感參數的2倍）的電流THD為4.19%。

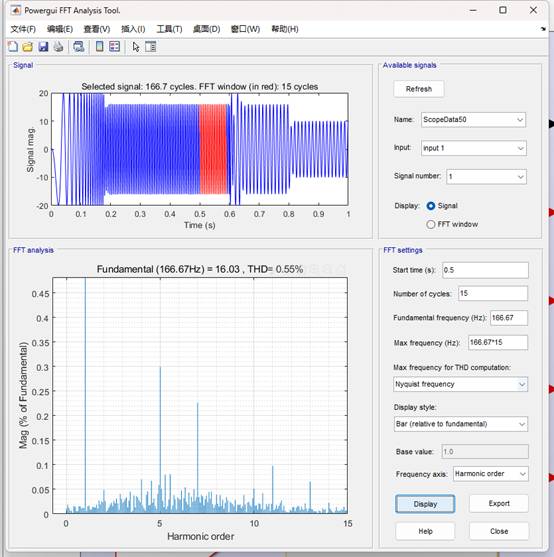
基于LESO的MFPCC（控制器中的電感參數設置為實際電感參數）

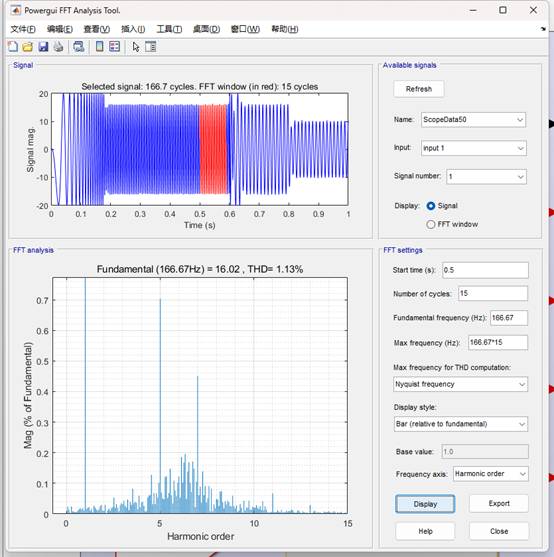
基于數據驅動的MFPCC

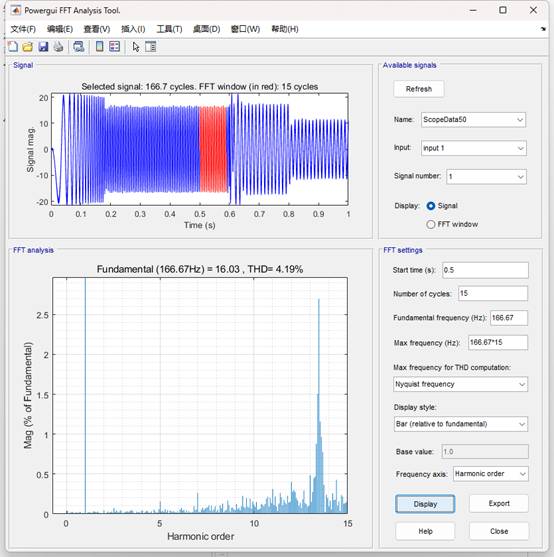
基于LESO的MFPCC（控制器中的電感參數設置為實際電感參數的2倍）

4.3 變速條件下電流的跟蹤情況

在0.6s的時候設置了電機減速，所以q軸電流的參考值會直接達到負的最大值（-20A）。從大體上來看，基于LESO的MFPCC（控制器中的電感參數設置為實際電感參數）和基于數據驅動的MFPCC的電流跟蹤情況非常接近。

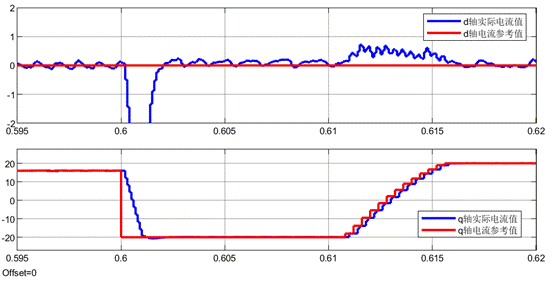
基于LESO的MFPCC（控制器中的電感參數設置為實際電感參數）

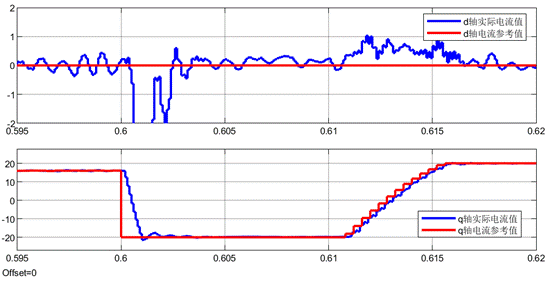
基于數據驅動的MFPCC

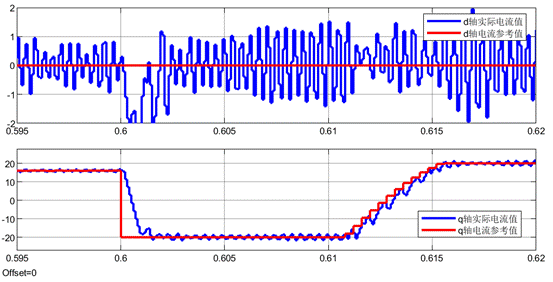
基于LESO的MFPCC（控制器中的電感參數設置為實際電感參數的2倍）

5.總結與思考

總結

本篇文章學習并復現了一篇基于數據驅動的MFPCC，該方法僅需要極短時間的數據即可構建出電機模型，并且以此模型進行閉環控制。該算法不需要任何電機參數即可實現較為優異的控制性能（THD略高于無參數失配條件下的LESO-MPFCC且動態性能基本一致），個人認為這樣性能還是比較優異的。

思考

在電機控制領域，相關算法感覺才處于剛起步的階段。這篇文章，我認為在個方面說的都比較詳細了，其實仔細看文章內容并去思考，會發現還有許多可以完善的地方。

雖然在仿真中，這基于數據驅動的MFPCC略微弱于無參數失配條件下的LESO-MPFCC，但是如果換個角度去看，比如說遇到一個多相的、磁場較為復雜的電機，其數學模型是較為復雜。如果人為的去建模，很可能無法構建精確的模型，也就無法人為的設計出性能較為優異的控制算法。這時候的基于數據驅動的MFPCC是否會更好呢？